南京大学：《电磁学》课程电子教案（教学课件）第九章 麦克斯韦方程与电磁波

厦电磁学0901：麦克斯韦方程组 ▣多类边界条件 电介质边界条件 Du D2>En=E2 i:(D2-D)=0,i×(E2-E)=0 磁介质边界条件 Ba=Be:Hn=H2 n(B2-B)=0,n×(H2-H)=0 导体界面电荷条件 -(i-)=-o 高频情况下真空界 i=Kn=ixH外 面条件 表面 导体内部

电磁学09-01: 麦克斯韦方程组  多类边界条件  电介质边界条件  磁介质边界条件  导体界面电荷条件  高频情况下真空界 面条件 1 21 2 2 1 21 , ( ) 0, ( ) 0 DDEE n ntt nD D n E E             1 21 2 21 2 1 , ( ) 0, ( ) 0 BBHH nn t t nB B n H H               0 02 01 nj j ( ) t         m i k nH       外

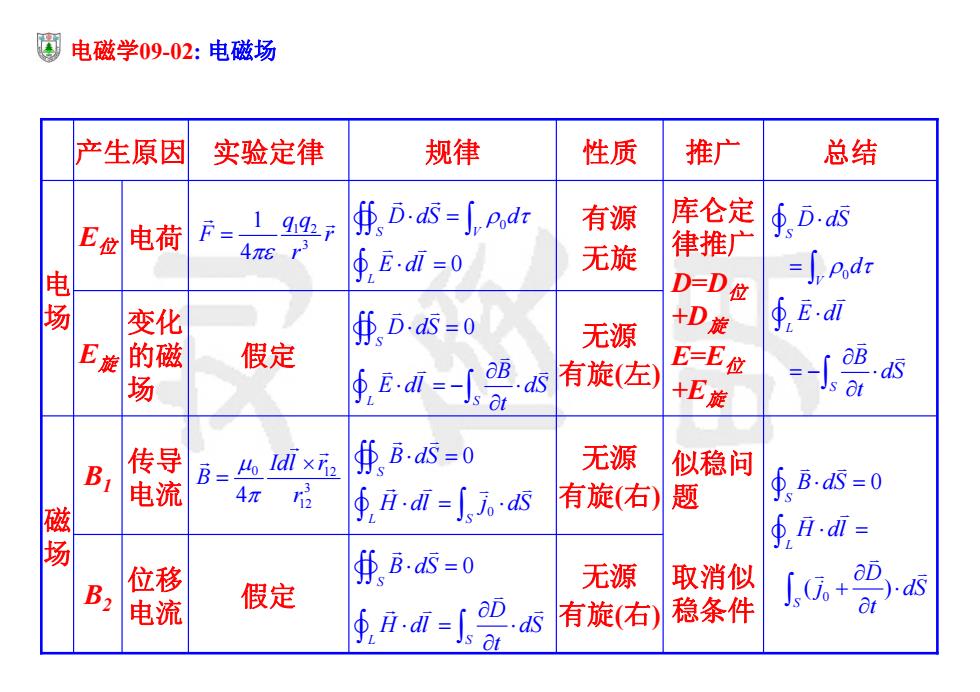
电磁学09.02：电磁场 产生原因 实验定律 规律 性质 推广 总结 有源 库仑定 E位电荷 F=19 ∯DS=∫pdr ∮D-as 4πer3 ∮Edi=0 无旋 律推广 D-D位 =5,Podr 场 变化 ∯Da否=0 无源 +D旋 ∮E-n E旋的磁 假定 E=E位 场 ∮i- B5有旋（左） +E旋 aB.dS 无源 Bi 传导 B=凸团× ∯B5=0 似稳问 电流 4π ∮H:i=〔j 有旋（右） 题 ∮B5=0 磁 ∮月dl= 位移 fB5=0 无源 取消似 B2 )d5 电流 假定 ∮idi= D d 有旋（右） 稳条件 +9 )s at

电磁学09-02: 电磁场 似稳问 题 取消似 稳条件 无源 有旋(右) 传导 电流 B1 库仑定 律推广 D=D位 +D旋 E=E位 +E旋 有源 无旋 E位 电荷 B2 E旋 无源 有旋(右) 假定 位移电流 磁 场 无源 有旋(左) 假定 变化 的磁 场 电 场 产生原因 实验定律 规律 性质 推广 总结 1 2 3 1 4 q q F r  r    0 0 S V L D dS d E dl                0 S L S D dS B E dl dS t                   0 12 3 12 4 Idl r B r        0 0 S L S B dS H dl j dS                 0 S L S B dS D H dl dS t                   0 S V L S D dS d E dl B dS t                       0 0 () S L S B dS H dl D j dS t                    

圈电磁学09.03：电磁波的数学 ▣ 一些物理基础实验现象： ▣Dipole Antenna Microwave Interference 高 Microwave Polarization Telegraph Transmitter

电磁学09-03: 电磁波的数学  一些物理基础实验现象：  Dipole Antenna  Microwave Interference  Microwave Polarization  Telegraph Transmitter

电磁学09.03：电磁波的数学 口波动方程：无自由电荷、无传导电流、各向同性 V.D=Po V,E=0 D=E0EE VxE=- aB aH 8t P=0 了×E=-44 V.B=0 B=MouH V.i=0 aD 8t j6=0 V×H=6 OE 8t 口绝好的相似性、对称性、关联性！

电磁学09-03: 电磁波的数学  波动方程：无自由电荷、无传导电流、各向同性 0 0 0 0 0 0 0 0 0 0 0 0 0 D E B H j D E B H E E t t B H D E H j H t t                                                                              绝好的相似性、对称性、关联性！

厦电磁学09.03：电磁波的数学 A×(B×C) >激动人心的变换之一： 电场波动 =(4.C)B-(4.B)C V×(V×高=VV.-vEV-E=0=-v元 如果初始电场 VxE--m aH aH Vx(VxE)=V 或磁场取空间 波的形式，则 其一定会自发 .-7E=V× aH 在空间传播！ 一一1 OE a(aE V×H=6E-VE=-(40c6 T.E=0 at at V×E=-4 oH .VE=(4μ)(88 a2E,1/-(44eE)12E at v.i=0 v2 8t2 OE V×H=6o8 aE I =v22E 4=1,8=1 in vacuum OE 0r2 8t2 =c2V2E

电磁学09-03: 电磁波的数学  激动人心的变换之一：电场波动 2 2 2 0 0 2 0 0 2 0 00 2 2 0 0 2 0 0 1/ ( ( )( ) ( ) ( ) , ( )( ) ( )( ) E v E EE E H H E E t t H E H t t E E H E t tt E E t                                                                                                      2 2 22 22 2 2 2 2 2 0 1, 1 in vacuum )( ) 1 E E vE cE t t E v t                        ( ) ( )( ) A BC A CB A BC             如果初始电场 或磁场取空间 波的形式，则 其一定会自发 在空间传播！ 0 0 0 0 E H E t H E H t                            