
提纲 一、历史和特点 二、定义和代数结构 2.1定义 2.2代数结构 三、Tanner图 四、构造 五、译码 六、随机LDPC码
提纲 一、历史和特点 二、定义和代数结构 2.1 定义 2.2 代数结构 三、Tanner图 四、构造 五、译码 六、随机LDPC码

2.1定义 定义1:(y,p)规则(regular)儿DPC码定义为具有如下特性的校验 矩阵HXw的零空间: (1)每一行含有p个1; (2)每一列含有y个1; (3)任两列之间位置相同的1的个数入=0,1 (4)p<<N,<J(低密度) (注意,HXw的各行并不要求独立) 密度r=pn=J
2.1 定义 定义1:( , )规则(regular)LDPC码定义为具有如下特性的校验 矩阵HJXN的零空间: (1) 每一行含有个1; (2) 每一列含有 个1; (3) 任两列之间位置相同的1的个数=0,1 (4) << N ,<< J (低密度) (注意,HJXN的各行并不要求独立) 密度r = /n = /J

2.1定义 0 00000011010001 定义:(y,p)规则 0 00000011010 0 0 (regular))LDPC码定义 1 001 01 0 0 为具有如下特性的校验 0 0 00000 0 矩阵HXN的零空间: 0 0 1 (1) 每一行含有p个1; 1 0 001000000 0 0 100010000000 1 (2) 每一列含有y个1; 1 0 010 0 1 (3) 任两列之间位置相同的 1 1 010 1 0 1的个数几=0,1; 0 110100010000 0 0 0 0110100010 0 4④p<N,<J(低密度) 0 001101000 100 0 0 0 000 1 10 100010 0 0 00000110100010 0 0 00000110100010 (15,7,5)LDPC码
2.1 定义 定义:( , )规则 (regular)LDPC码定义 为具有如下特性的校验 矩阵HJXN的零空间: (1) 每一行含有个1; (2) 每一列含有 个1; (3) 任两列之间位置相同的 1的个数=0,1; (4) << N ,<< J (低密度) 0 0 0 0 0 0 1 1 0 1 0 0 0 1 0 0 0 0 0 0 1 1 0 1 0 0 0 1 0 0 0 0 0 0 1 1 0 1 0 0 0 1 0 0 0 0 0 0 1 1 0 1 0 0 0 1 0 0 0 0 0 0 1 1 0 1 0 0 0 1 0 0 0 0 0 0 1 1 0 1 0 0 0 1 0 0 0 0 0 0 1 1 0 1 0 0 0 1 0 0 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 0 0 0 0 1 1 1 0 0 0 1 0 0 0 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0 0 0 1 1 0 1 0 0 1 0 0 0 0 0 0 0 1 1 0 1 0 0 1 0 0 0 0 0 0 0 1 1 0 1 0 0 1 0 0 0 0 0 0 0 1 1 0 1 0 0 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 1 (15,7,5) LDPC码
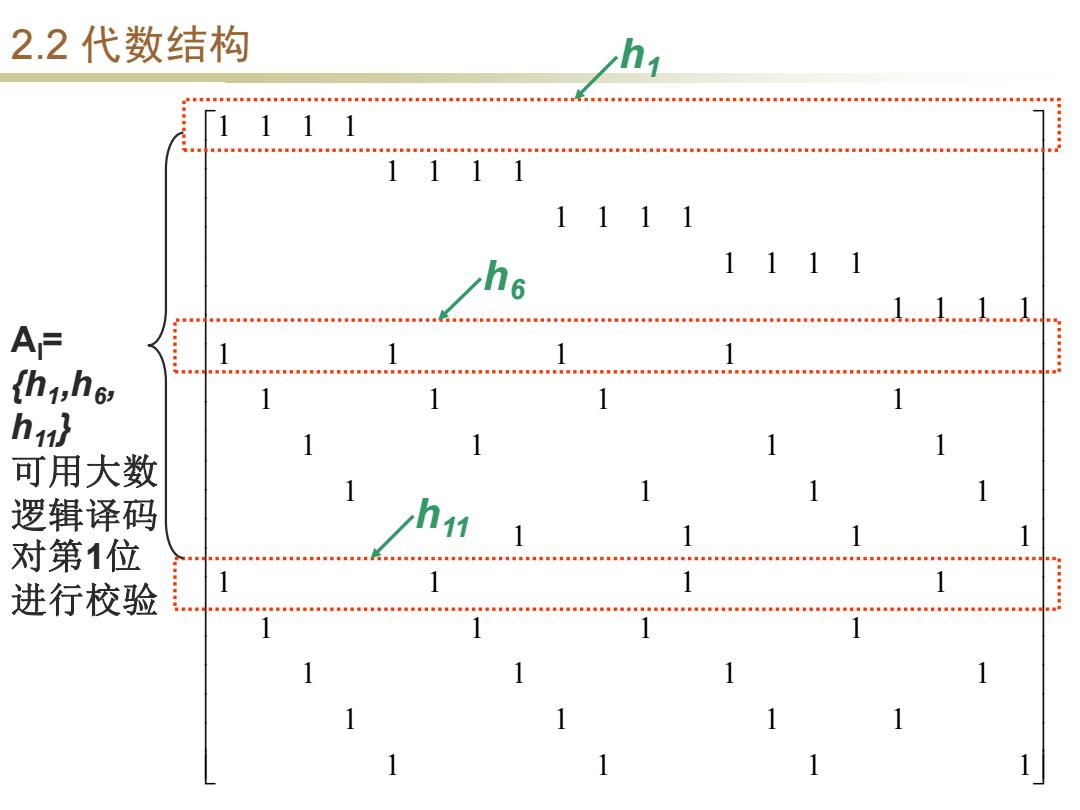
2.2代数结构 111 111 1111 1111 A= thi,h6 hu} 可用大数 逻辑译码 对第1位 进行校验 1 1 1 1 1 1
2.2 代数结构 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 Al= {h 1 ,h 6 , h11} 可用大数 逻辑译码 对第 1 位 进行校验 h 1 h 6 h11
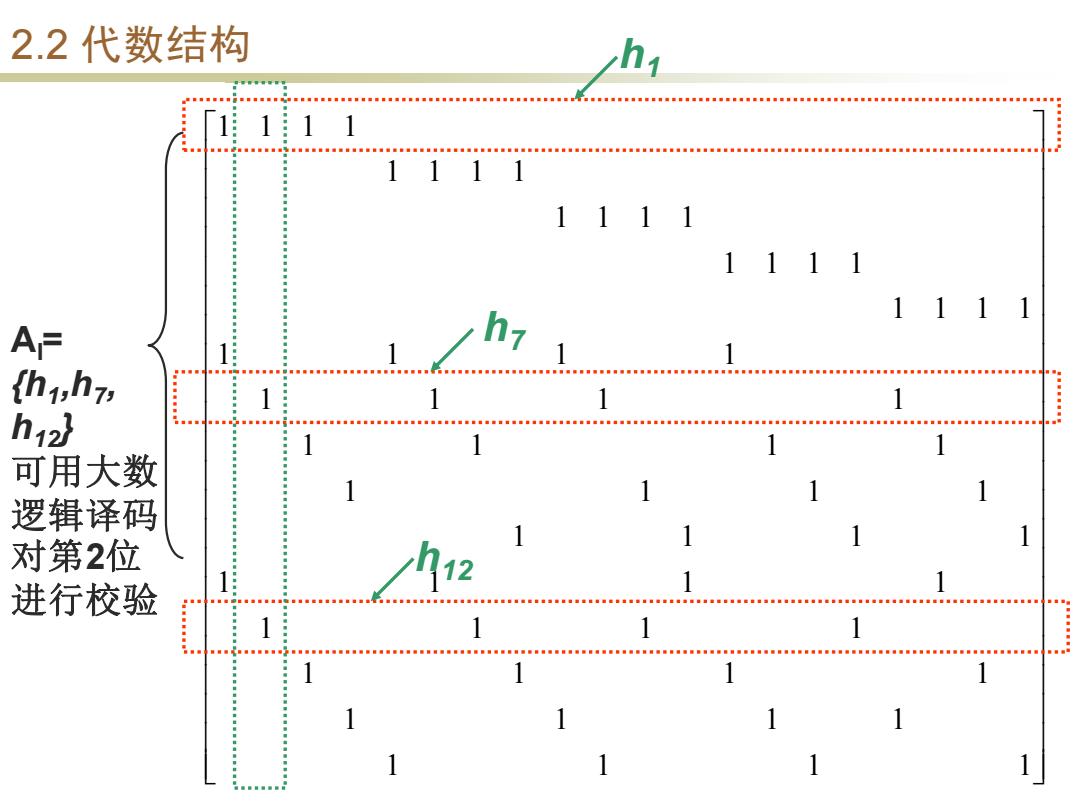
2.2代数结构 1 1111 1111 1111 A= h1,h7) 1 1 h12} 可用大数 1 逻辑译码 1 对第2位 2 1 进行校验 1 1 1 1 1 1 1 1 1 1 1
2.2 代数结构 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 Al= {h1 ,h7 , h12} 可用大数 逻辑译码 对第2位 进行校验 h1 h7 h12