
例2长途汽车起点站于每时的10分、30分、 55分 发车,设乘客不知发车时间,于每小时的任意时 刻随机地到达车站,求乘客的平均候车时间 0 J030 22 e0 解:设乘客于某时X分到达车站,候车时间为Y,则 10-X0≤X<10 fx(x)= 0<x<60 30-X10≤X≤30 60 Y=g(X)= others 55-X30≤X<55 1 60 70-X55≤X<60 E(Y)= 60 8(x)d =10分25秒
例2 长途汽车起点站于每时的10分、30分、55分 发车,设乘客不知发车时间,于每小时的任意时 刻随机地到达车站,求乘客的平均候车时间 解:设乘客于某时X分到达车站,候车时间为Y,则 − − − − = = 70 55 60 55 30 55 30 10 30 10 0 10 ( ) X X X X X X X X Y g X = others x f x X 0 0 60 60 1 ( ) = 60 0 ( ) 60 1 E(Y) g x dx =10分25秒

1 i 设X服从N(0,1)分布,求E(X2),E(X3),E(X4) f(x)=2元 2 00 E(X2)= -de 2 2元 2d=1
设X服从N(0,1)分布,求E(X2 ),E(X3 ),E(X4 ) 2 2 2 1 ( ) x f x e − = e dx x E X x 2 2 2 2 2 ( ) − − = 2 2 2 x de x − − = − e dx x 2 2 2 1 − − = = 1
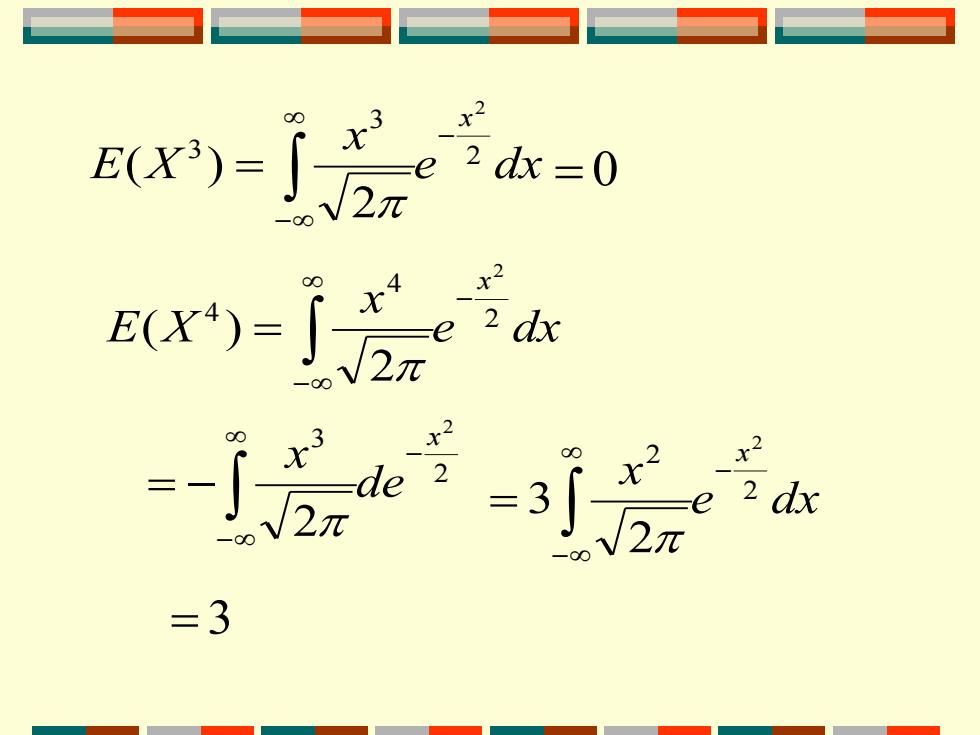
-1 r? =3
e dx x E X x 2 3 3 2 2 ( ) − − = = 0 e dx x E X x 2 4 4 2 2 ( ) − − = 2 3 2 2 x de x − − = − e dx x x 2 2 2 2 3 − − = = 3

四数学期望的性质(P78) 1.E(c)=c,c为常数; 2。E(cX)=cE(X),c为常数; 证明:设X~fx),则 E(cX)-jaxf(xds =c∫xf(x)dk=cE(X)
1. E(c)=c,c为常数; 2。E(cX)=cE(X), c为常数; 四.数学期望的性质(P78) 证明:设X~f(x),则 − E(cX ) = cxf (x)dx = c x f (x)dx = cE(X ) −

3.E(X+Y)=E(X)+E(Y); 证明:设(X,Y)~fk,y) E(X+Y)=∫∫(x+y)f(x,y)dd =了jfx,+∫「f(x, -00-00 -jxff(x.y)dvldxt jxjr(x.y)dxldy -f(x +f(vy+E)
3. E(X+Y)=E(X)+E(Y); 证明:设(X,Y)~f(x,y) − − E(X +Y) = (x + y) f (x, y)dxdy − − = x f (x, y)dxdy − − + yf (x, y)dxdy x[ f (x, y)dy]dx − − = − − + y[ f (x, y)dx]dy x f x dx X − = ( ) yf y dy Y − + ( ) = E(X ) + E(Y)