版权©2019,版权保留,侵犯必究 例题1 如图所示,已知信号频率为50Hz,纵坐标每格表示 10V。请写出各电压的瞬时表达式。 V2 V3 v1为参考相量V,=20c0s(100πt)V V2=30c0s(100Tt-T/4)VV3=10cos(100Tt-T/2)V 复旦大学射频集成电路设计研究小组 -017- 唐长文
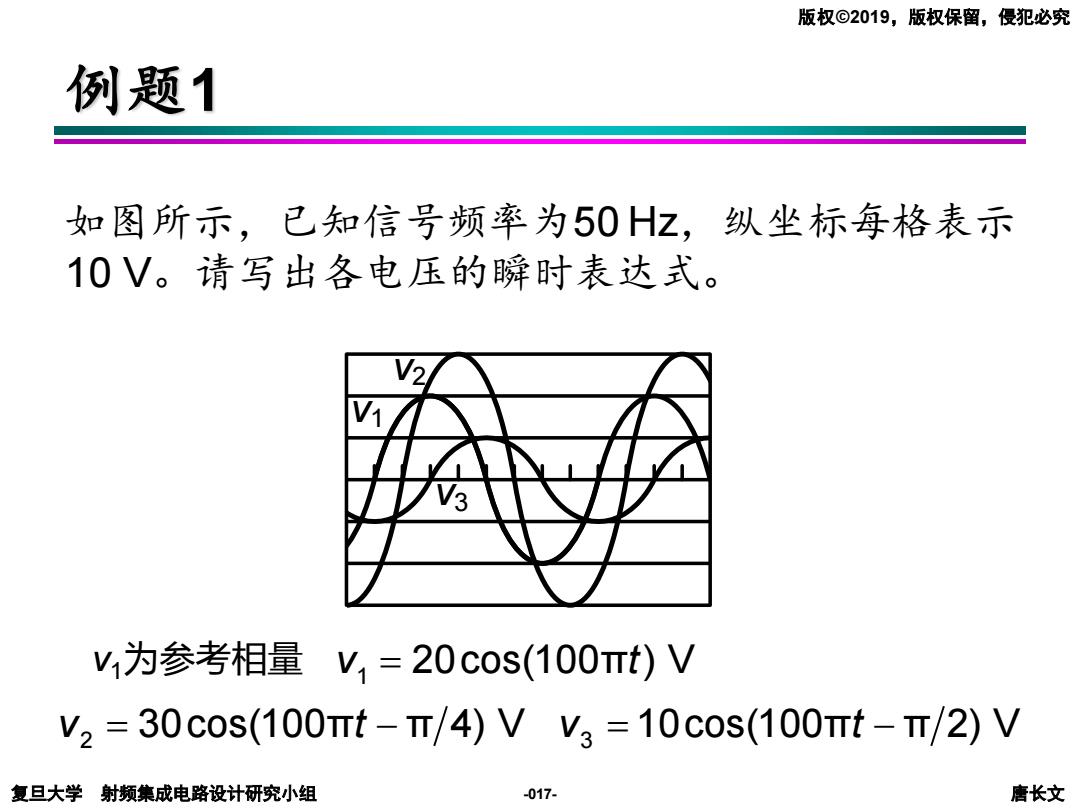
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -017- 例题1 如图所示,已知信号频率为50 Hz,纵坐标每格表示 10 V。请写出各电压的瞬时表达式。 v1 v2 v3 v1为参考相量 v t 1 = 20cos(100π ) V v t 2 = − 30cos(100π π 4) V v t 3 = − 10cos(100π π 2) V
版权©2019,版权保留,侵犯必究 例题2 如图所示电路,电阻R=12,电感L=1H,电容C =1F,电压源Vs=COs(),试计算电压VR,和VC。 KVL方程 +VR-+M一 VR+VL +VC=VS 0000 R+ldt=cos0 di R 假设i=mcos(t+p) /m=1,=0,VR cos(f),VL =-sin(f)=cos(t+TT/2) Vc sin(t)=cos(t-TT/2) 复旦大学射频集成电路设计研究小组 -018- 唐长文
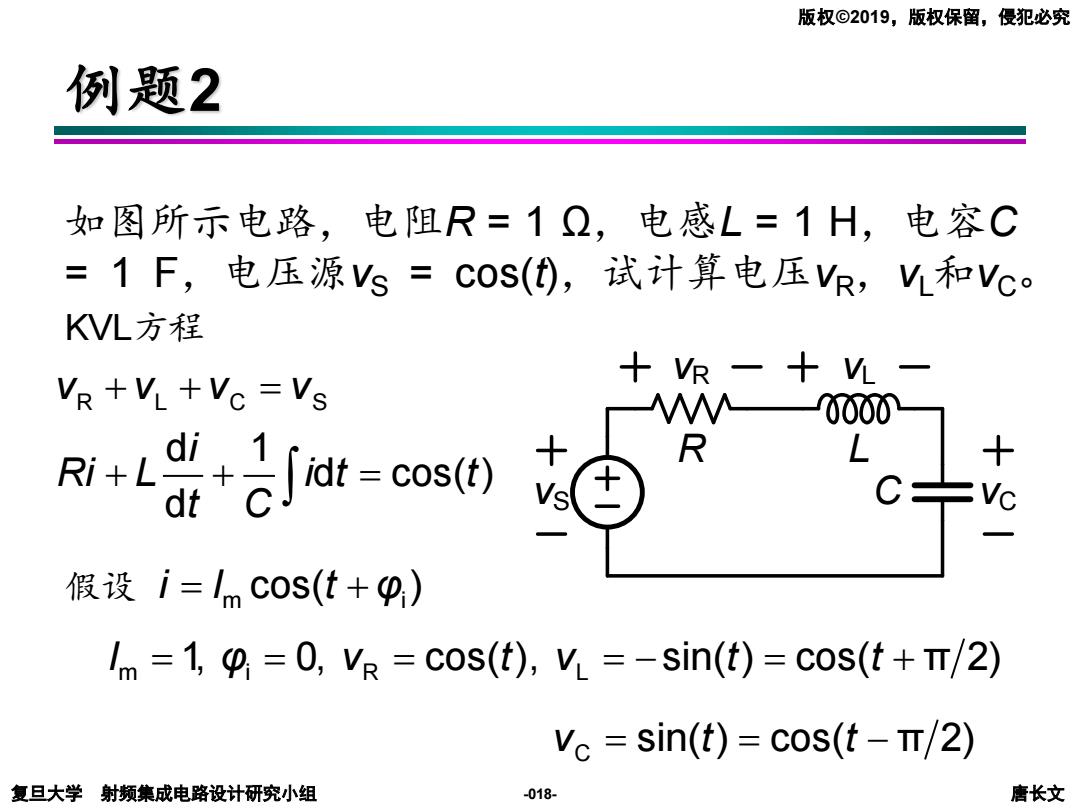
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -018- 例题2 如图所示电路,电阻R = 1 Ω,电感L = 1 H,电容C = 1 F,电压源vS = cos(t),试计算电压vR,vL和vC。 KVL方程 假设 R L C S d 1 d cos( ) d v v v v i Ri L i t t t C + + = + + = m i i I t = + cos( ) φ Im i R L = = = = − = + 1, 0, cos( ), sin( ) cos( φ v t v t t π 2) C v t t = = − sin( ) cos( π 2) vS vR vL vC R L C

版权©2019,版权保留,侵犯必究 利用欧拉公式求解 ei〔wt+9)+ewt+g) 根据欧拉公式Vi cos(wt+p,)=Vm 2 RLC串联电路 Ri+Lt di dt cSidt-ve eie) ew+)+e+) m 2 2 ei(wt+p)+ejwt+p) +jwL)) Im ei(wu)) ei(wt+g)+e-j(wt+9) m 2 2 jwC 2 2 +aL+ce=Vea Ve Rl-aL-ale-Vee R+jLiC) 复旦大学射频集成电路设计研究小组 -019- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -019- 利用欧拉公式求解 根据欧拉公式 RLC串联电路 i i j( ) -j( ) m i m e e cos( ) 2 ωt φ ωt φ V ωt φ V + + + + = i i j( ) -j( ) j( ) -j( ) S m m e e e e , 2 2 ωt φ ωt φ ωt φ ωt φ v V i I + + + + + + = = S d 1 d d i Ri L i t v t C + + = i i j( ) - j( ) j( ) - j( ) j( ) - j( ) j( ) - j( ) m m m m e e e e e e e e j 2 2 j 2 2 ωt φ ωt φ ωt φ ωt φ ωt φ ωt φ ωt φ ωt φ I RI I ωL V ωC + + + + + + + + + − − + + + = i i m j( ) j( ) m m m m -j( ) -j( ) m m m ( j )e e j ( j )e e j ωt φ ωt φ ωt φ ωt φ I RI I ωL V ωC I RI I ωL V ωC + + + + + + = − − = i j j m m e e 1 ( j ) j φ φ V I R ωL ωC = + +
版权©2019,版权保留,侵犯必究 正弦量的相量变换 相量变换 A=PIA cos(wt +)]=Ael=An 相量反变换f(t)=P-[Ae]=A cos(wt+p) 正弦量与相量的关系 +1 t=0 ωt t=t1 Am cos(wt+p)=P-(Ame)=Re(Aeiw)=(Aei+Ae-iwt )/2 复旦大学射频集成电路设计研究小组 0110- 唐长文
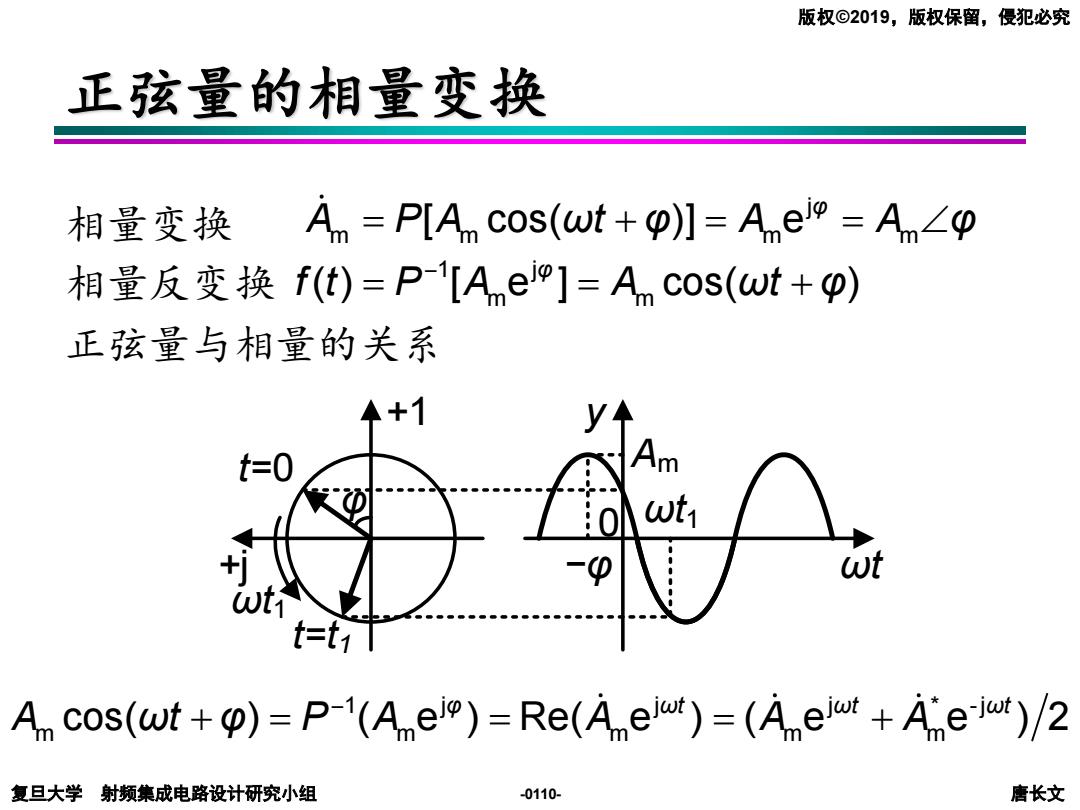
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -0110- 正弦量的相量变换 相量变换 相量反变换 正弦量与相量的关系 j m m m m [ cos( )] e φ A P A = + = = ωt φ A A φ 1 j m m ( ) [ e ] cos( ) φ f t P A A ωt φ − = = + y ωt 0 Am −φ t=0 +1 +j t=t1 ωt1 ωt1 φ 1 j j j * -j m m m m m cos( ) ( e ) Re( e ) ( e e ) 2 φ ωt ωt ωt A ωt φ P A A A A − + = = = +

版权©2019,版权保留,侵犯必究 相量变换的性质 ·线性叠加性 P[a,f(t)+a22(t)]=a,P[f(t)]+a2P[f(t)] P-ila Am+a2An2]=aP-[Am]+a2P[Ami] ·微分性 P91=ioP-tl-jA ·积分性 P时a-e- jω 复旦大学射频集成电路设计研究小组 -0111- 唐长文
复旦大学 射频集成电路设计研究小组 唐长文 版权©2019,版权保留,侵犯必究 -0111- 相量变换的性质 • 线性叠加性 • 微分性 • 积分性 1 1 2 2 1 1 2 2 1 1 1 m1 2 m2 1 m1 2 m1 [ ( ) ( )] [ ( )] [ ( )] [ ] [ ] [ ] P a f t a f t a P f t a P f t P a A a A a P A a P A − − + = + + = +m d ( ) [ ] j [ ( )] j d f t P ωP f t ωA t = = m [ ( )] [ ( )d ] j j P f t A P f t t ω ω = =