
1家庭作业·数学·九年级·下册·配北师大版 .AB=BC=10米. 【方法归纳】 在Rt△DBC中,:∠CDB=30, 作“两高”构造出直角三角形和矩形,是 BC DB-tan 2CDB-10/3() 解有关梯形问题时的一般思路;当两个直角 DH=AH-(DB-AB)=10-103+ 三角形有公共边时,先求出这条公共边是解 10=20-105≈2.7(米),2.7<3, 答此类题的一般思路. 该建筑物需要拆除 新知·训练巩固 1.已知某斜坡的坡角为a,坡度i=3:4,则 的垂直距离DE=50米(点A,B,C,D,E在 sina的值为(B). 同一平面内),在点D处测得建筑物顶点A A B号 c号 D. 的仰角为50°,则建筑物AB的高度约为(D). (参考数据:sin50°≈0.77,cos50°≈0.64, 2.如图,一辆小车沿坡角为α的斜坡向上行 tan50°≈1.19) 驶了13米,已知cosa= 则小车上升的 高度是(A). A.69.2米 B.73.1米 A.5米B.6米C.6.5米D.12米 C.80.0米 D.85.7米 3.如图,在建筑物AB左侧距楼底点B水平 4.一条上山直道的坡度为1:7,沿这条直道上 距离150米的C处有一山坡,斜坡CD的 山,每前进100米所上升的高度为10√2米. 坡度(或坡比)为i=1:2.4,坡顶D到BC 素能·演练提升 1.如图,一堤坝的迎水面 D i=1:3 A.31.2m B.26.5m DC与水平面的夹角为A C.25.2m D.24.2m 40°(∠DCE=40°),现将堤坝迎水面改为 2.小明想测量一棵树的 AB,坡度为1:3,其中水平宽度加宽BD为 高度,他发现树的影子 4m,AC为19.2m,则新的迎水面AB的长约 恰好落在地面和一个 309 为(B).(参考数据:sin40°≈0.64, 斜坡上,如图.此时测得地面上的影长为 cos40°≈0.77,tan40°≈0.84,√/10≈3.16) 8米,坡面上的影长为4米.已知斜坡的坡角 为30°,同一时刻,一根长为1米、垂直于地 24

第一章直角三角形的边角关系\ 面放置的标杆在地面上的影长为2米,则 与河堤下端C之间的距离是1.5米. 树的高度为(A). 7.日照间距系数反映了房屋日照情况.如图 A.(6十√5)米 B.12米 (1),当前后房屋都朝向正南时,日照间距 C.(4+23)米 D.10米 系数=L:(H一H),其中L为楼间水平 3.如图,为了测量某 距离,H为南侧楼房高度,H为北侧楼房 建筑物BC的高 底层窗台至地面高度, 度,小颖采用了如 下的方法:先从与 建筑物底端B在 同一水平线上的点A出发,沿斜坡AD行 走130米至坡顶D处,再从D处沿水平方 图(1) 图(2) 向继续前行若干米后至点E处,在点E测 如图(2),山坡EF朝北,EF长为15m,坡 得该建筑物顶端C的仰角为60°,建筑物底 度为i=1:0.75,山坡顶部平地EM上有 端B的俯角为45°,点A,B,C,D,E在同一 一高为22.5m的楼房AB,底部A到点E 平面内,斜坡AD的坡度i=1:2.4.根据 的距离为4m. 小颖的测量数据,计算出建筑物BC的高度 (1)求山坡EF的水平宽度FG: 约为(A).(参考数据:√3≈1.732) (2)欲在AB楼正北侧山脚的平地FV上建 A.136.6米 B.86.7米 一楼房CD,已知该楼底层窗台P处至 C.186.7米 D.86.6米 地面C处的高度为0.9m,要使该楼的 4.如图,某水库大坝的横断面是梯形ABCD, 日照间距系数不低于1.25,底部C距F 坝顶宽AD=6米,坝高是20米,背水坡 处至少多远? AB的坡角为30°,迎水坡CD的坡度为 解(1)在Rt△EFG中,,∠G=90, 1:2,那么坝底BC的长度等于46+20√3 tan∠ErG上1:075-争器 米.(结果保留根号) 设EG=4xm,则FG=3xm, .EF√EG+FG=5x 6 .EF=15,∴.5x=15,X=3, ∴.FG=3X=9, 即山坡EF的水平宽度FG为9m. (第4题图) (第5题图) (2).L=CF+FG+EA=CF+9+4= 5.如图,斜坡AB的坡度i=1:2,坡脚B处 CF+13,H=AB+EG=22.5+12=34.5, 有一棵树BC,某一时刻测得树BC在斜坡 H1=0.9, AB上的影子BD的长度为10米,这时测 .日照间距系数=L:(H-H)= 得太阳光线与水平线的夹角为60°,则树 CF+13CF+13 BC的高度为2√5+4V15米. 34.5-0.933.6 6.小明坐于堤边垂钓,如 ·该楼的日胎间距系数不低于1.25, 图,河堤AC的坡角为 0069≥125cF≥29, 30aC的长为39米。 水平线 C B ∴,要使该楼的日照间距系数不低于 钓竿OA的倾斜角是60°,其长为3米,若 1.25,底部C距F处至少29m远. OA与钓鱼线OB的夹角为60°,则浮漂B 25

儿家庭作业·数学·九年级·下册·配北师大版 利用三角函数测高 基础·自主梳理 1.测量倾斜角 (1)测量倾斜角可以用测倾器.简单的 测倾器由度鑫、铅锤和支杆组成 (如图). P 3.测量底部不可以到达的物体的高度 39 (1)所谓“底部不可以到达”,就是在地面 上不能直接测得测点与被测物体的底部之 间的距离。 (2)使用测倾器测量倾斜角的步骤如下: (2)如图,要测量物体MV的高度,可按 ①把支杆竖直插入地面,使支杆的中心 下列步骤进行: 线、铅垂线和度盘的0°刻度线重合,这时度 ①在测点A处安置测倾器,测得此时M 盘的顶线PQ在水平位置 的仰角∠MCE=a. ②转动度盘,使度盘的直径对准目标M, ②在测点A与物体之间的B处安置测倾 记下此时铅垂线所指的度数即可. 器(A,B与N在一条直线上,且A,B之间的 2.测量底部可以到达的物体的高度 距离可以直接测得),测得此时M的仰角 (1)所谓“底部可以到达”,就是在地面上 ∠MDE=B. 可以无障碍地直接测得测点与被测物体的 ③量出测倾器的高度AC=BD=a, 底部之间的距离。 以及测点A,B之间的距离AB=b. (2)如图,要测量物体MN的高度,可按 根据以上测量数据,便能求出物体MN 下列步骤进行: 的高度为a+ btan o·tan tan B-tan o ①在测点A处安置测倾器,测得M的仰 角∠MCE=a. ②量出测点A到物体底部V的水平距 离AN=I. ③量出测倾器的高度AC=a. 根据以上测量数据,便能求出物体MV 的高度为a+Itan o· 26

第一章直角三角形的边角关系\ 核心·重难探究 知识点:测量底部不可以到达的物体的 BD...tan 42.0= AD AD BD ≈0.9,AD≈0.9BD. 高度 【例题】如图,山顶 在Rt△BCD中,tan∠CBD= CD BD 上有一个信号塔AC,已 .'.tan 36.9= CD 知信号塔高AC=15米, BD ≈0.75, 在山脚下点B处测得塔 ∴.CD≈0.75BD. D 底C的仰角∠CBD=36.9°,塔顶A的仰角 .AC=AD-CD,..15=0.15BD ∠ABD=42.0°,求山高CD(点A,C,D在同 ∴.BD=100(米),∴.CD=0.75BD=75(米). 一条竖直线上).(参考数据:tan36.9°≈ 答:山高CD约为75米. 0.75,sin36.9°≈0.60,tan42.0°≈0.90) 【方法归纳】 思路点拨在Rt△ABD和Rt△BCD 解决这类问题首先要找到相关联的直角 中,分别用BD表示出AD和CD,利用AC= 三角形,当图形中没有直角三角形时,要通过 15米,求得BD的长,进而求出CD, 作高或垂线构造直角三角形,正确利用锐角 解由题意,在Rt△ABD中,tan∠ABD= 三角函数求解即可. 新知·训练巩固 1.在一次数学活动中,李 离BC为30m,在点A测得 明利用一根拴有小锤的 点D的仰角∠EAD=45°,在 细线和一个半圆形量角 点B测得点D的仰角 E60 器制作了一个测角仪, B D ∠CBD=60°,则甲、乙这两座 去测量学校内一座假山的高度CD.如图, 建筑物的高度分别为(D. 已知小明距假山的水平距离BD为12m, A.10√/5m,30m 他的眼睛距地面的高度为1.6m,李明的视 B.30m,30√3m 线经过量角器零刻度线OA和假山的最高 点C,此时,铅垂线OE经过量角器的60°刻 C.(30√/3-3)m,30m 度线,则假山的高度为(A). D.(30√5-30)m,30√5m A.(4√3+1.6)m B.(12√3+1.6)m 3.如图,小明用自制的直角三角形纸板DEF C.(4√2+1.6)m D.4√5m 测量树的高度AB,他调整自己的位置,设 2.如图,甲、乙为两座建筑物,它们之间的水平距 法使斜边DF保持水平,并且边DE与点B 27
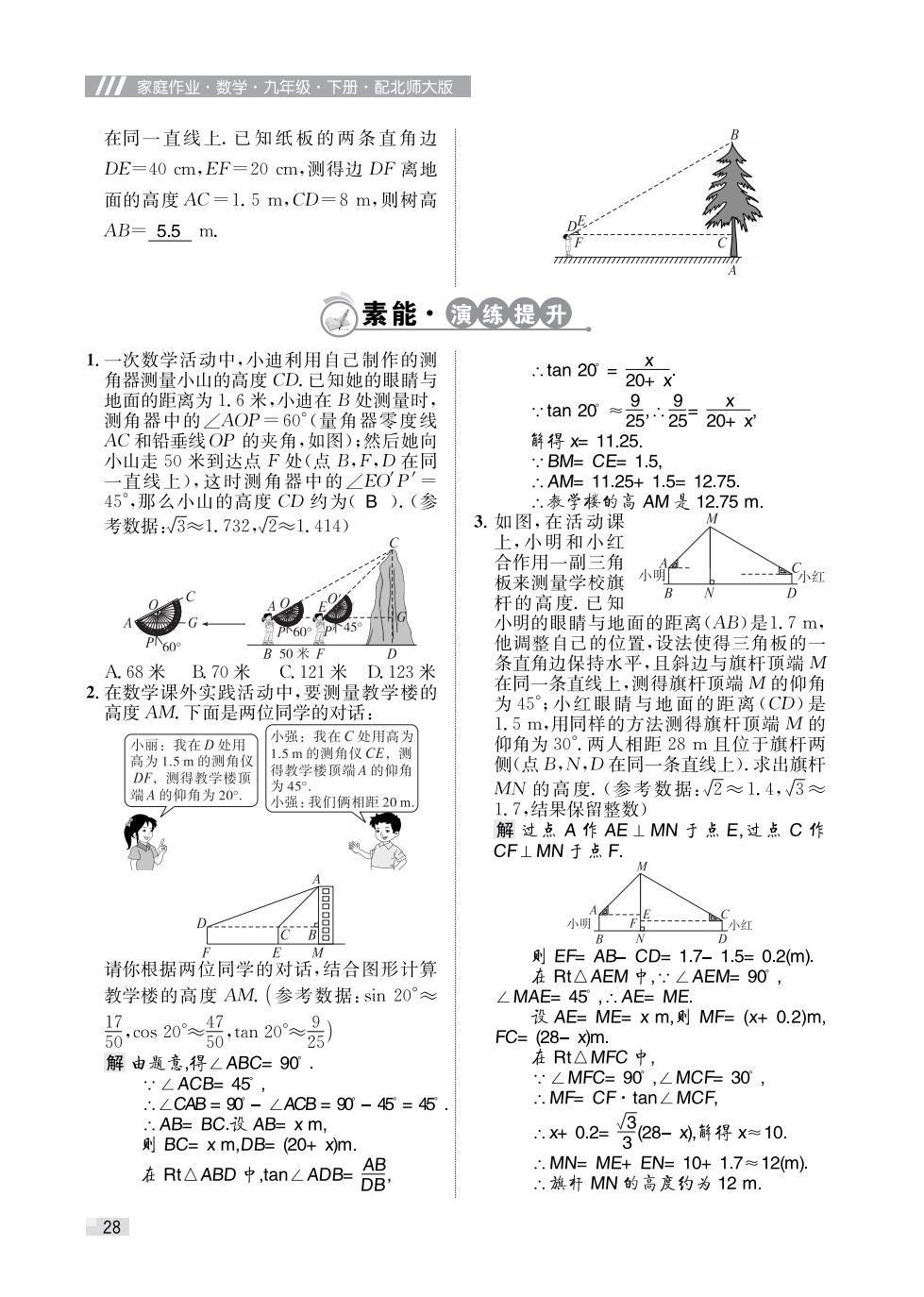
儿家庭作业·数学·九年级·下册·配北师大版 在同一直线上.已知纸板的两条直角边 DE=40cm,EF=20cm,测得边DF离地 面的高度AC=1.5m,CD=8m,则树高 AB=5.5m. 7777777777717777777777777777177 ☑素能·演练提升 1.一次数学活动中,小迪利用自己制作的测 X 角器测量小山的高度CD.已知她的眼睛与 ∴.tan20= 20+X 地面的距离为1.6米,小迪在B处测量时, 9.9 X 测角器中的∠AOP=60°(量角器零度线 :tan20≈252520+X AC和铅垂线OP的夹角,如图);然后她向 解得X=11.25. 小山走50米到达点F处(点B,F,D在同 .:BM=CE=1.5, 一直线上),这时测角器中的∠EOP' ∴.AM=11.25+1.5=12.75, 45°,那么小山的高度CD约为(B).(参 .表学楼的高AM是12.75m. 考数据:√5≈1.732,√2≈1.414) 3.如图,在活动课 M 上,小明和小红 合作用一副三角 板来测量学校旗 小明 外红 杆的高度.已知 B D 7P60° p45 小明的眼睛与地面的距离(AB)是1.7m, P60 他调整自己的位置,设法使得三角板的一 B50米F A.68米B.70米C.121米D.123米 条直角边保持水平,且斜边与旗杆顶端M 2.在数学课外实践活动中,要测量教学楼的 在同一条直线上,测得旗杆顶端M的仰角 高度AM.下面是两位同学的对话: 为45°;小红眼睛与地面的距离(CD)是 1.5m,用同样的方法测得旗杆顶端M的 小强:我在C处用高为 小丽:我在D处用 仰角为30°.两人相距28m且位于旗杆两 高为1.5m的测角仪 1.5m的测角仪CE,测 侧(点B,N,D在同一条直线上).求出旗杆 DF,测得教学楼顶 得教学楼顶端A的仰角 为45°, 端A的仰角为20°. MN的高度.(参考数据:√2≈1.4,√3≈ 小强:我们俩相距20m 1.7,结果保留整数) 解过点A作AE⊥MN于点E,过点C作 CF⊥MN于点F S小红 E 小明F 则EFAB-CD=1.7-1.5=0.2m: 请你根据两位同学的对话,结合图形计算 在Rt△AEM中,.∠AEM=90, 教学楼的高度AM.(参考数据:sin20°≈ ∠MAE=45°,.∴.AE=ME. oas20品am20号》 17 设AE=ME=xm,则MF=(x+0.2)m, FC=(28-xm. 解由意,得∠ABC=90. 在Rt△MFC中 .∠ACB=45°, .∠MFC=90,∠MCF=30, ∴.∠CAB=90-∠ACB=90-45°=45 .∴MF=CF·tan∠MCF .AB=BC.设AB=Xm, 则BC=xm,DB=(20+xm. x402=写28-双销得x10 在Rt△ABD中,tan/ADB=侣, .MN=ME+EN=10+1.7≈12m DB ∴.旗杆MN的高度约为12m. 28