
第一章直角三角形的边角关系\ 2.已知∠a为锐角,且sima-,则∠a 8.已知&是锐角,且si血(a十15)-,计算 (A). A.30° B.45° C.60° D.90° 8-4cosa-(x-3.14)°+tana+(3) 3.计算:√tan30°-2tan30°+1+tan30°= 的值 (D). 解s动60- A.2 n251 .+15°=60. .a=45. C.25-1 D.1 4.如图,A,B,C是小正方形 原浅=22-4号141+38 的顶点,且每个小正方形的 9.如图,在离水面高度 边长都为1,则tan∠BAC (AC)为2米的岸上有 的值为(B). 人用绳子拉船靠岸,开 30 B A司 B.1 c D.√3 始时绳子与水面的夹角为30°,此人以每秒 0.5米的速度收绳子 5.已知∠C=75°,则∠A与∠B满足以下哪 问:(1)未开始收绳子的时候,图中绳子BC 个选项才能构成△ABC?(C). 的长度是多少米? AmA-号mB=号 2 (2)收绳2秒后船离岸边多少米? 解(1)如图,在Rt△ABC中, B.cos A=-号,cosB-Y9 2 ..sin 30 AC BC C.sin A= 2,tan B=/3 ..BC= 2 sin30=4(米). nmA-号asB号 (2)如图所示, 6.如图,△ABC的顶点 B,C的坐标分别是 30>A 、30 (1,0),(0,3),且 D ∠ABC=90°,∠A= 设收绳2秒后在点D位置.收绳2秒 30°,则顶点A的坐标是(43)· 后,绳子BC缩短了0.5×2=1(米),此时绳 7.(2022·贵州安顺中考)计算:(一1)2+ 子只有3米,即CD=3米. (π-3.14)°+2sin60°+|1-√3|-√12. 在Rt△ACD中,AD=JCD2-AC2= 解(-1}+(π-3.14)°+2sin60°+11- √32-22=√5(米). 1-E-=1+1+29原-1-2ge 收绳2秒后船离岸边√5米. 2+√3+5-1-23=1. 9

家庭作业·数学,九年级·下册·配北师大版 三角函数的计算 基础·自主梳理 1.用科学计算器求三角函数值,要用到 三角函数值 按键顺序 显示结果 sincos tan键. SHI▣sin sin-10.9816= sina=0.9816 例如,求sin23°,cos23°15'27"和tan155 @gg06▣ 78.99184039 的按键顺序如下表所示: SHIF▣cos c0s10.8607= 三角函数 按键顺序 显示结果 cos3=0.8607 回0@G0☑包 30.60473007 sin 23" sn23▣ 0.390731128 SHIFT tan tan-156.78= cos 23 tanY=56.78 c0s2315'27 0.91873953 60叼▣ 88.99102049 网2☑包 (2)上表的结果是以“度”为单位的;再 tan 155 an0固网固-包 0.269508666 按”键即可显示以“度、分、秒”为单位的 2.已知三角函数值求角度,要用到sin 结果 costan键的第二功能“sin-1,cos1,tan-1”和 3.当从低处观测高处的目标时,视线与 SHIFT 水平线所成的锐角称为仰角· 4.当从高处观测低处的目标时,视线与 (1)例如,已知sina=0.9816,cos3= 0.8607,tany=56.78,求∠a,∠3,∠y的度 水平线所成的锐角称为俯角: 数的按键顺序如下表所示: 核心·重难探究 知识点一:用科学计算器求三角函数值 .tan321624≈0.6315. 【例1】用计算器求值: 【方法归纳】 (1)sin50°:(2)cos23.57°:(3)tan3216'24. 思路点拨用计算器求三角函数值时,计 已知锐角求三角函数值,按照正确的按 键顺序按键,将屏幕显示的结果按要求取近 算结果一般精确到 位 似值即可. 解(1)按锭顺序:sin⑤回包: 显示:0.766044443: 知识点二:已知三角函数值求角度 .sin50≈0.7660; 【例2】已知下列各锐角的三角函数值, 2)楼篌顺序:cos2305☑=☐: 求这些锐角的大小(精确到1"). 显示:0.916572226: (1)sina=0.5018; ∴.c0s23.57≈0.9166; (2)cos3=0.6531: (3)tany=0.3750. (3)按锭顺序:an32四□6m24 思路点拨用计算器根据三角函数值求 四☐;显示:0.631522525; 角度时,计算结果一般精确到 10

第一章直角三角形的边角关系、 解(1)按锭顺序:SHIFT sin回⑤回□8 他又测得两建筑物之间的距离BC是28米, Em;显示:307g;a=307g 请你帮助小明求出建筑物CD的高度(结果精 确到1米). 2)按锭顺序:SHIF口cos回犯同53□=☐ 思路点拨(1)根据图中现有的三角形, ”;显示:491327; 能不能求出建筑物CD的高度? ∴.B=49°1327”.(3)按锭顺序:SHIFT (2)怎么构造直角三角形求建筑物CD的高度? tan003⑦⑤回=☐m;显:20°3322; 解过点A作AE⊥CD,垂足为点E, 由题意得,AE=BC=28, .Y=203322. ∠EAD=25,∠EAC=43. 【方法归纳】 在Rt△ADE中, 由三角函数值用计算器求角度,计算器 tanLEAD-,.DE=tan 2528 显示结果是以“度”为单位的,一般化为用 在Rt△ACE中,:tan/EAC= CE “度、分、秒”为单位的,用四键可实现两者间 .CE=tan43×28 的转换 .∴.DC=DE+CE=tan25°x28+ 知识点三:仰角、俯角 tan43×28≈39(米). 【例3】如图,小明的家在某住 D ..缝筑物CD的高度约为39米. 宅楼AB的最顶层(AB⊥BC),他 家的后面有一建筑物CD(CD∥ 【方法归纳】 AB),他很想知道这座建筑物的 B 解决有关仰角、俯角的解直角三角形的 高度,于是在自家阳台的A处测得建筑物CD 问题,先构造直角三角形,再借助角边关系、 的底部C的俯角是43°,顶部D的仰角是25°, 三角函数的定义求解即可. 新知·训练巩固 1.在角的度量单位为“”的状态下,求sin9的 为(B). 值,以下按键顺序正确的是(A). A.30° B.37° C.38 D.39 A.sing▣ B.回sin目 4.用计算器求值:sin18°+cos55°-tan59°. C.sim9oy目 D.回sin 0omm月 (写出按键顺序) 解在角的度量单位为“”的状态下,按锭 2.用计算器求sin20°+tan5433'的结果等于 顺序依次为:sn回⑧+cos⑤⑤-口 (结果精确到0.01)(D). A.2.25B.1.55C.1.73 D.1.75 tan⑤g=☐, 3.在Rt△ABC中,∠C=90°,a:b=3:4,运用 根据屏暮上显示的结果四舍五入,得 计算器计算,∠A的度数(结果精确到1) sin18+cos55-tan59≈-0.7817. 11

儿家庭作业·数学·九年级·下册·配北师大版 素能·演练提升 1.如图,在△ABC中,∠C= 7”日, 90°,∠B=42°,BC=8,若 根据屏暮上显示的结果四舍五入得 用科学计算器求AC的长,则下列按键顺 sin8.7-cos5436+tan51°47'≈0.71; 序正确的是(D). 2)按锭顺序依次为:tan24☐⑤x☒ A.⑧日sin42目B.⑧日cos42▣ tan6⑤肥⑤=☐,根据屏暮上显示的结果四 c.⑧日tan42目D.⑧☒tan42目 舍五入得tan24.5×tan65.5=1. 2.用计算器验证,下列不等式中成立的是 6.如图,学校的实验楼对面是一幢教学楼,小 (B). 敏在实验楼的窗口C处测得教学楼顶部D A.sin 3724>cos 3724'+cos 310' 处的仰角为18°,教学楼底部B处的俯角为 B.cos 4532>sin 45-sin 112' 20°,教学楼的高BD=21m,求实验楼与教 C.sin63°47'<cos1821'-cos87° 学楼之间的距离AB.(结果保留整数) D.2sin30°12'<sin60241 D 3.某商场营业大厅自动扶梯的示意图如图所 示.自动扶梯AB的倾斜角为37°,大厅两 层之间的距离BC为6米,则自动扶梯AB B 的长约为(sin37°≈0.6,cos37°≈0.8, 解过点C作CM⊥BD于点M, tan37°≈0.75)(D). DM A 在Rt△CDM中,tan DCM= A.7.5米B.8米C.9米D.10米 CM 4.一个直角三角形有两条边长分别为3,4,则较 .∴D作CM×tan∠DCM CM×tan18 小的锐角约为37或41.(结果精确到1) 在Rt△BCM中,:tan BCM=B% CM' 5.用计算器求下列各式的值.(写出按键顺 .BM=CMx tan∠BCM=CM×tan20°. 序,结果精确到0.01) DM+BM=BD, (1)sin8.7°-cos5436'+tan51°47'; .CMx tan 18 CMx tan 20 21, (2)tan24.5×tan65.5. 21 解在角的度量单位为“”的状态下, 解得CM-tan18+tan20≈30m,. (1)按镜顺序依次为:sin8☐⑦因- ∴.AB=CM≈30m,即AB的长约为30m. cos54四3回”+an⑤□”4 12
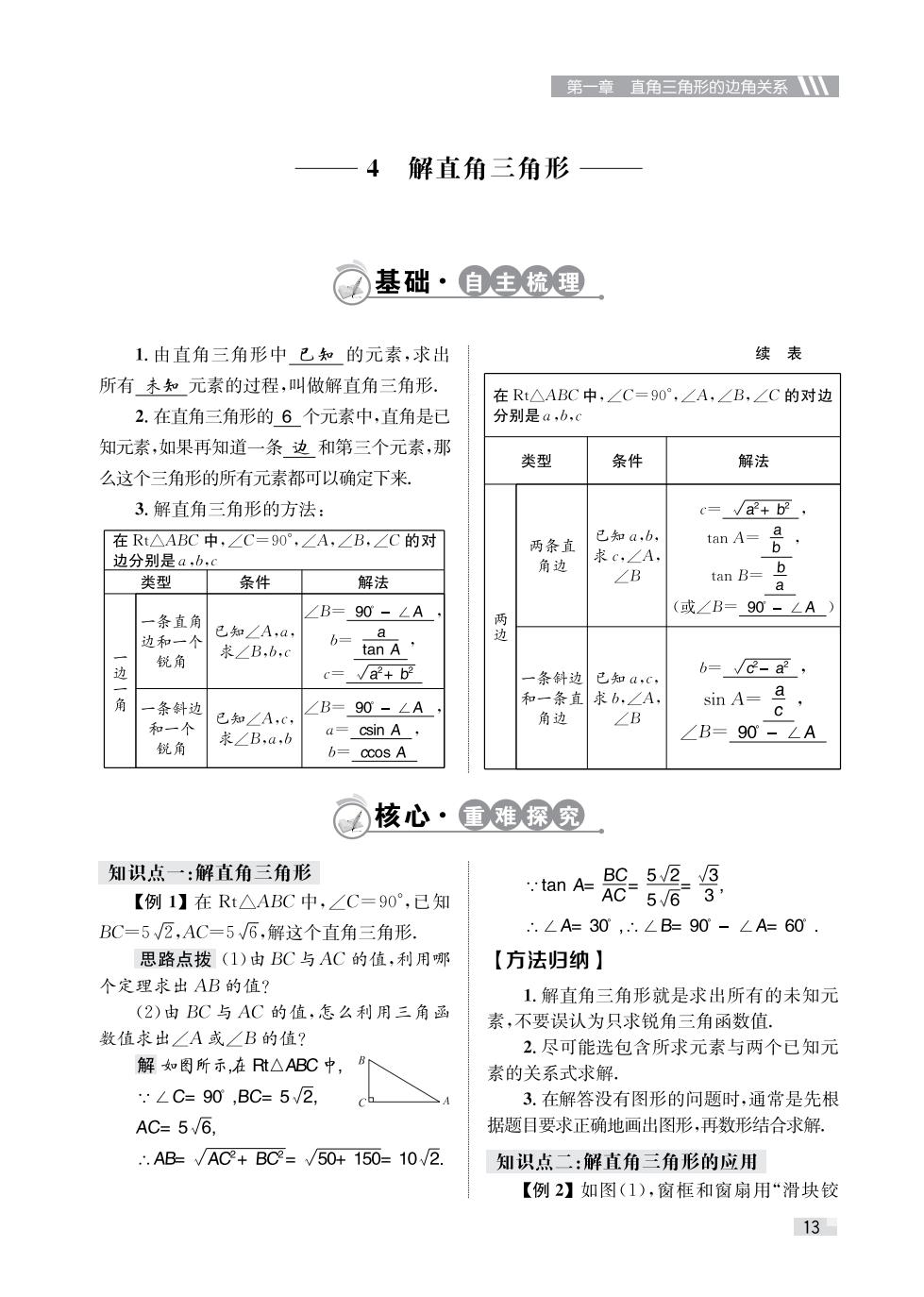
第一章 直角三角形的边角关系\ 4解直角三角形 基础·自主梳理 1.由直角三角形中已知的元素,求出 续表 所有未知元素的过程,叫做解直角三角形 在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边 2.在直角三角形的6个元素中,直角是已 分别是a,b,c 知元素,如果再知道一条边和第三个元素,那 类型 条件 解法 么这个三角形的所有元素都可以确定下来 3.解直角三角形的方法: c=a+b2, 在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对 两条直 已知a,b, 边分别是a,b,c 求c,∠A, amA=是, 角边 类型 条件 解法 ∠B tan B=b a ∠B=90-∠A (或∠B=90-∠A) 一条直角 两 边和一个 已知∠A,a, b= a 求∠B,b,c tan A, 边 锐角 c=W√a2+b 一条斜边 已知a,c b=-a, 和一条直 求b.∠A sin A= a 角 一条斜边 ∠B=90-∠A 已知A,c, 角边 和一个 ∠B 求∠B,a,b a=csin A, ∠B=90-∠A 锐角 b=CCos A 核心·重难探究 知识点一:解直角三角形 .tan A= BC.523 【例1】在Rt△ABC中,∠C=90°,已知 AC563, BC=5√2,AC=5√6,解这个直角三角形. ∴.∠A=30,.∠B=90°-∠A=60. 思路点拨(1)由BC与AC的值,利用哪 【方法归纳】 个定理求出AB的值? 1.解直角三角形就是求出所有的未知元 (2)由BC与AC的值,怎么利用三角函 素,不要误认为只求锐角三角函数值, 数值求出∠A或∠B的值? 2.尽可能选包含所求元素与两个已知元 解如图所示,在Rt△ABC中, 素的关系式求解. ∠C=90,BC=5√2, 3.在解答没有图形的问题时,通常是先根 AC=5√6, 据题目要求正确地画出图形,再数形结合求解. ∴.AB=√JAC+BC=√50+150=10√2. 知识点二:解直角三角形的应用 【例2】如图(1),窗框和窗扇用“滑块铰 13