
Review:Potential-based Proof Proof.Recall the(worst-case regret)analysis of Hedge.We present a 'potential-based'proof, where the potential is defined as =(-+立m ≤-p,+n∑p, (n(1+x)≤x)】 重-重-1≤-p,)+n∑P,, 2=1 Advanced Optimization(Fall 2023) Lecture 8.Adaptive Online Convex Optimization 16
Advanced Optimization (Fall 2023) Lecture 8. Adaptive Online Convex Optimization 16 Review: Potential-based Proof
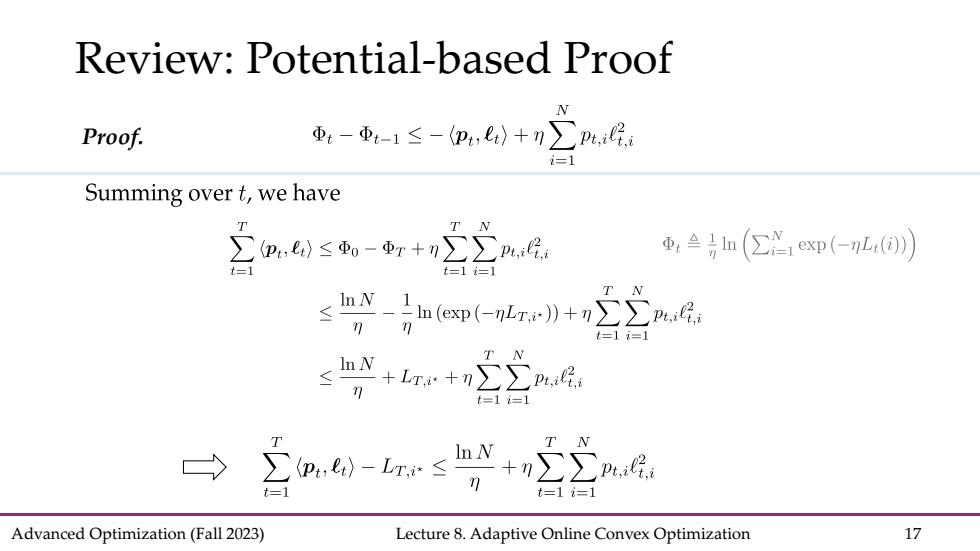
Review:Potential-based Proof Proof. 重:-重-1≤-(p4,)+n∑p,i2 i=1 Summing over t,we have m≤-r+上之,民 T 重,1n(Y1exp(←nl()) t三1i=1 ≤nN-n(ep(-r》+n∑∑. 0 =1= T N t=1=1 ∑p,e)-L≤血N+ n∑∑ t=1 t=1=1 Advanced Optimization(Fall 2023) Lecture 8.Adaptive Online Convex Optimization 17
Advanced Optimization (Fall 2023) Lecture 8. Adaptive Online Convex Optimization 17 Review: Potential-based Proof Proof

Improved Analysis for Small-Loss Bound Proof. t=1i=1 For previous worst-case analysis,we simply utilize et.i<1: T pu.i≤nI To get a small-loss bound,we improve the analysis to be: TN T n∑∑Pu:呢:≤n∑∑P=n∑p, t=1i=1 t=1i=1 T T +n∑p,) t=1 Advanced Optimization(Fall 2023) Lecture 8.Adaptive Online Convex Optimization 18
Advanced Optimization (Fall 2023) Lecture 8. Adaptive Online Convex Optimization 18 Improved Analysis for Small-Loss Bound Proof