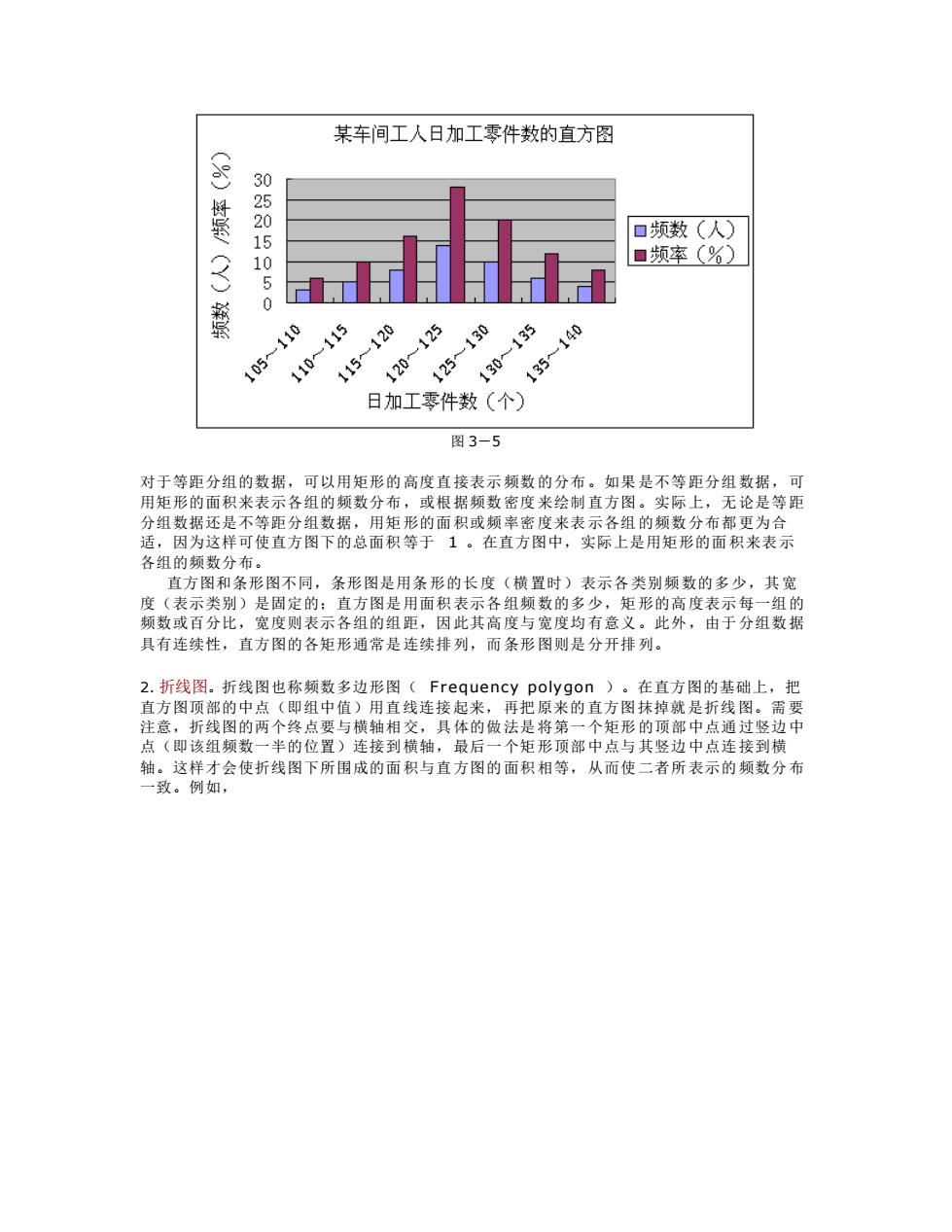
某车间工人日加工零件数的直方图 20250 16 口频数(人) 10 ■频率(%) 50 105 日加工零件数(个) 图3-5 对于等距分组的数据,可以用矩形的高度直接表示频数的分布。如果是不等距分组数据,可 用矩形的面积来表示各组的频数分布,或根据频数密度来绘制直方图。实际上,无论是等距 分组数据还是不等距分组数据,用矩形的面积或频率密度来表示各组的频数分布都更为合 适,因为这样可使直方图下的总面积等于1。在直方图中,实际上是用矩形的面积米表示 各组的频数分布。 直方图和条形图不同,条形图是用条形的长度(横置时)表示各类别频数的多少,其宽 度表示类别)是固定的:直方图是用面积表示各组 频数的多少,矩形的高度表示每 一组野 百分比,霓度则 示各组的组距,因此其高 宽度均有意义。此外,由于分组数据 具有连续性,直方图的各矩形通常是连续排列,而条形图则是分开排列。 2.折线图。折线图也称频数多边形图(Frequency polygon)。在直方图的基础上,把 直方图顶部 (即组中 )用直线连接起来 把原来的直方图抹掉就是折线图 意即该组 的两 半的位置) 项 接到
图 3-5 对于等距分组的数据,可以用矩形的高度直接表示频数的分布。如果是不等距分组数据,可 用矩形的面积来表示各组的频数分布,或根据频数密度来绘制直方图。实际上,无论是等距 分组数据还是不等距分组数据,用矩形的面积或频率密度来表示各组的频数分布都更为合 适,因为这样可使直方图下的总面积等于 1 。在直方图中,实际上是用矩形的面积来表示 各组的频数分布。 直方图和条形图不同,条形图是用条形的长度(横置时)表示各类别频数的多少,其宽 度(表示类别)是固定的;直方图是用面积表示各组频数的多少,矩形的高度表示每一组的 频数或百分比,宽度则表示各组的组距,因此其高度与宽度均有意义。此外,由于分组数据 具有连续性,直方图的各矩形通常是连续排列,而条形图则是分开排列。 2. 折线图。折线图也称频数多边形图( F requency polygon )。在直方图的基础上,把 直方图顶部的中点(即组中值)用直线连接起来,再把原来的直方图抹掉就是折线图。需要 注意,折线图的两个终点要与横轴相交,具体的做法是将第一个矩形的顶部中点通过竖边中 点(即该组频数一半的位置)连接到横轴,最后一个矩形顶部中点与其竖边中点连接到横 轴。这样才会使折线图下所围成的面积与直方图的面积相等,从而使二者所表示的频数分布 一致。例如

10510115120125130135140 日加工零件数(个) 图3-6 当对数据所分的组数很多时,组距会越来越小,这时所绘制的折线图就会越来越光滑,逐渐 形成一条平滑的曲线,这就是频数分布曲线。分布曲线在统计学中有着十分广泛的应用,是 描述各种统计量和分布规律的有效方法, (二)时间序列数据:线图 据,以反映事物发展变化的规律和趋势。 3-3:191一198年国乡民家的人均收入数如下表所示试制线 1991一1998年域多居民京房人均收入 单位:元 年份 城镇居民 农村居民 1991 1700.6 708.6 1992 2026.6 784 1993 25774 9216 100 3496.2 1221 1905 4283 1557.7 1996 4838.9 1926.1 1997 5160.3 2091.1 1998 5425.1 2162 资科来源:《中国统计摘要1999》,78页,北京,中国统计出版社,1999, 表3一7
图 3-6 当对数据所分的组数很多时,组距会越来越小,这时所绘制的折线图就会越来越光滑,逐渐 形成一条平滑的曲线,这就是频数分布曲线。分布曲线在统计学中有着十分广泛的应用,是 描述各种统计量和分布规律的有效方法。 (二)时间序列数据:线图 如果定距数据和定比数据是在不同时间上取得的,即时间序列数据,还可以绘制线图。线图 是在平面坐标上用折线表现数量变化特征和规律的统计图。线图主要用于显示时间序列数 据,以反映事物发展变化的规律和趋势。 例 3-3 : 1991 - 1998 年我国城乡居民家庭的人均收入数据如下表所示。试绘制线 图。 表 3-7