
环行图:和圆形图相比,环行图可以同时绘制多个总体的数据系列,从而有利于进行多个总 体的比段研究· 13万7% 口非常不满意 10%18% 口不满意 ☐一般 ■满意 31 囚非常满意 26 图3-4
环行图:和圆形图相比,环行图可以同时绘制多个总体的数据系列,从而有利于进行多个总 体的比较研究。 图 3-4

第三节数值型数据的整理与显示 前述定类数据和定序数据的整理和图示方法都适用于数值型数据的整理和显示,下述数值型 数据的一些特定整理和图示方法并不适用于品质数据。 一,数据的分组 将数值型数据进行数据分组就是将数据按照某种标准化分成不同的组别。分组后再计算出各 组中出现的次数或频数,就形成了一张频数分布表。分组的方法有单变量值分组和组距分组 两种。 一)单变量值分组 单变量值分组就是把每一个变量值作为一组,它一般只适用于离散变 量且变量值较少的情况。 例3-2某生产车间50名工人日加工零件数(单位:个)。试采用单变量值对数据进行 分组。 117122124129139107117130 122125 108131125117 122133126 122 118108 110 118123126 133134127 123 118112 112 134 127123 119113120 123 127135 137114120128124115139128124121 为便于分组,可先对上面的数据进行排序,结果如下: 107108108110112112113114115117 117 117 118 118 118 119120 120 121122 122 122122123 123123123124 124.124 125 125126126 127 127127 128 128120 130131133133134134135137139139 采用单变量值分组形成的频数分布表如下表所示
第三节 数值型数据的整理与显示 前述定类数据和定序数据的整理和图示方法都适用于数值型数据的整理和显示,下述数值型 数据的一些特定整理和图示方法并不适用于品质数据。 一. 数据的分组 将数值型数据进行数据分组就是将数据按照某种标准化分成不同的组别。分组后再计算出各 组中出现的次数或频数,就形成了一张频数分布表。分组的方法有单变量值分组和组距分组 两种。 (一)单变量值分组。单变量值分组就是把每一个变量值作为一组,它一般只适用于离散变 量且变量值较少的情况。 例 3-2 某生产车间 50 名工人日加工零件数(单位:个)。试采用单变量值对数据进行 分组。 为便于分组,可先对上面的数据进行排序,结果如下: 采用单变量值分组形成的频数分布表如下表所示
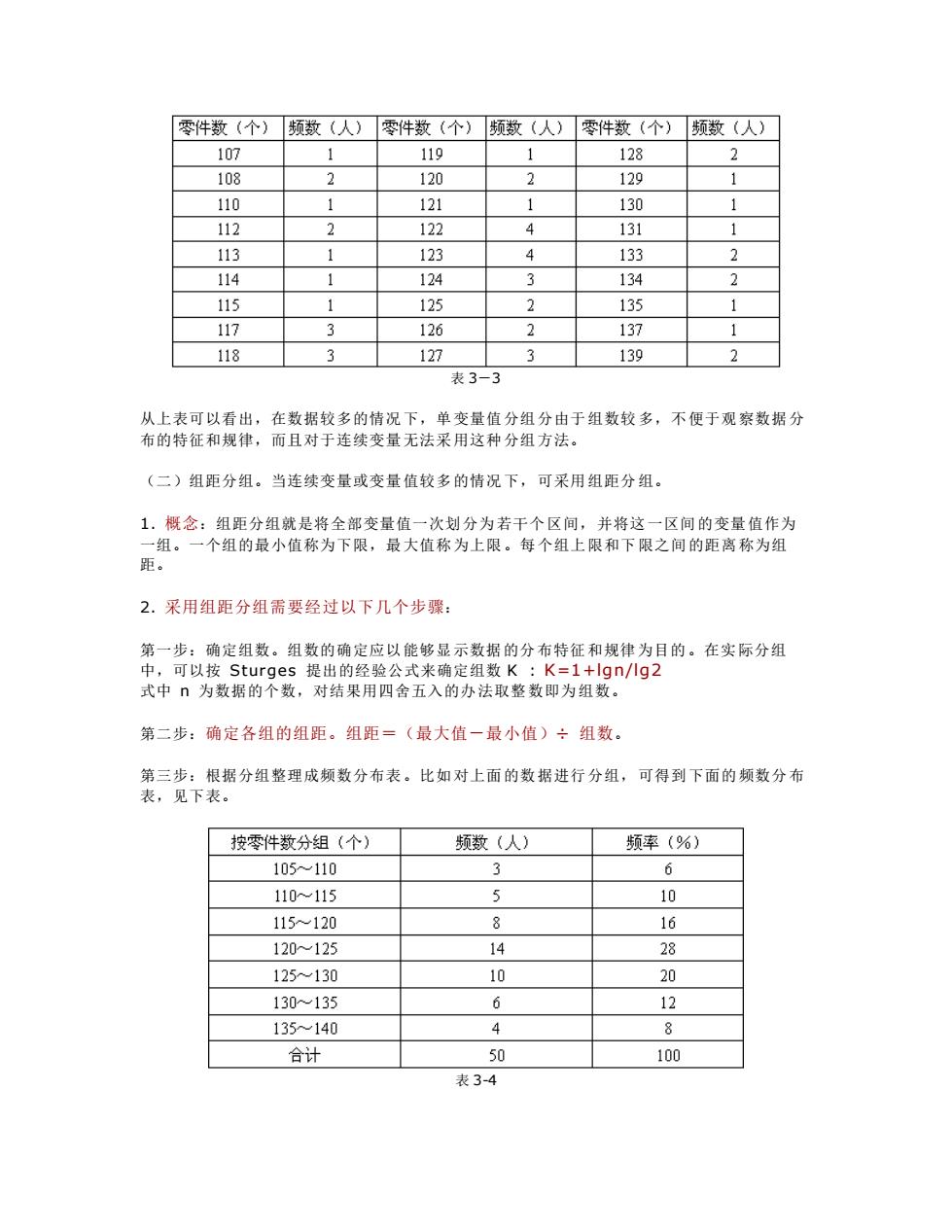
零件数(个)频数(人)零件数(个)频数(人)零件数(个)频数(人) 107 1 119 128 108 120 2 129 110 121 130 112 122 4 131 113 1 123 133 114 1 124 3 134 115 1 125 2 135 17 3 126 2 137 118 3 127 3 130 2 表3-3 从上表可以看出,在数据较多的情况下, 单变量值分组分由于组数较多,不便于观察数据分 布的特征和规律,而且对于连续变量无法采用这种分组方法。 (二)组距分组。当连续变量或变量值较多的情况下,可采用组距分组。 1.概念:组距分组就是将全部变量值一次划分为若干个区间,并将这一区间的变量值作为 组。一个组的最小值称为下限,最大值称为上限。每个组上限和下限之间的距离称为组 距。 2.采用组距分组需要经过以下几个步骤: 第一步:确定组数。组数的确定应以能够显示数据的分布特征和规律为日的。在实际分组 中,可以按Sturges提出的经验公式来确定组数K:K=1+lgn/小g2 式中为数据的个数,对结果用四舍五入的办法取整数即为组数。 第二步:确定各组的组距。组距=(最大值一最小值)÷组数。 第三步:根据分组整理成频数分布表。比如对上面的数据进行分组,可得到下面的频数分布 表,见下表。 按零件数分组(个) 频数(人) 频率(%) 105110 3 6 110115 10 115120 8 16 120~125 14 28 125130 10 20 130~135 6 12 135140 4 8 合计 50 100 表3-4
表 3-3 从上表可以看出,在数据较多的情况下,单变量值分组分由于组数较多,不便于观察数据分 布的特征和规律,而且对于连续变量无法采用这种分组方法。 (二)组距分组。当连续变量或变量值较多的情况下,可采用组距分组。 1. 概念:组距分组就是将全部变量值一次划分为若干个区间,并将这一区间的变量值作为 一组。一个组的最小值称为下限,最大值称为上限。每个组上限和下限之间的距离称为组 距。 2. 采用组距分组需要经过以下几个步骤: 第一步:确定组数。组数的确定应以能够显示数据的分布特征和规律为目的。在实际分组 中,可以按 Sturges 提出的经验公式来确定组数 K : K=1+lgn/lg2 式中 n 为数据的个数,对结果用四舍五入的办法取整数即为组数。 第二步:确定各组的组距。组距=(最大值-最小值)÷ 组数。 第三步:根据分组整理成频数分布表。比如对上面的数据进行分组,可得到下面的频数分布 表,见下表。 表 3-4
3.“不重不漏“原则。采用组距分组时,一定要遵循“不重不漏“的原则。“不重”是指一项数 锯只能分在中的菜一组,不能在其他组中重复出烫不福是指在所分的全部组别中每项梦 据都能 中的某 ,不能遗漏。为解决“不重”的问题,统计分组时习惯上规定“上组 在”组相两组的上 如, 对例3-2的数据做如下的分组 见下表 按零件数分组(个) 频数(人) 频率(%) 105109 6 110114 10 115~119 8 16 120124 14 28 125~129 10 20 130134 6 12 135~139 8 合计 50 100 表3-5 对于连续变量可以采取相邻两组组限重叠的方法,根据”上组限不在肉的规定解决~不重“的 1 可以对 的精度具体研 定。 例如 对零件尺寸可以分组为 等等 如果全部数据中的最大值和最小值与其他数相差悬殊, 变量值的组)或个别极端 组可以采取“XX 以下 常以相邻组的组距作为其组距 进im inlina cla ="tite14x知">例子3-2假定将最小值改为94,最大值改为160,采用上面的分组就 会出现“空白组”,这时可采用开口组,见下表 按零件数分组(个) 频数(人) 频率(% 105以下 3 110~115 10 115120 16 120~125 14 28 125~130 10 20 130135 6 12 135以上 4 8 合计 0 100 表3- 5.等距分组和不等距分组
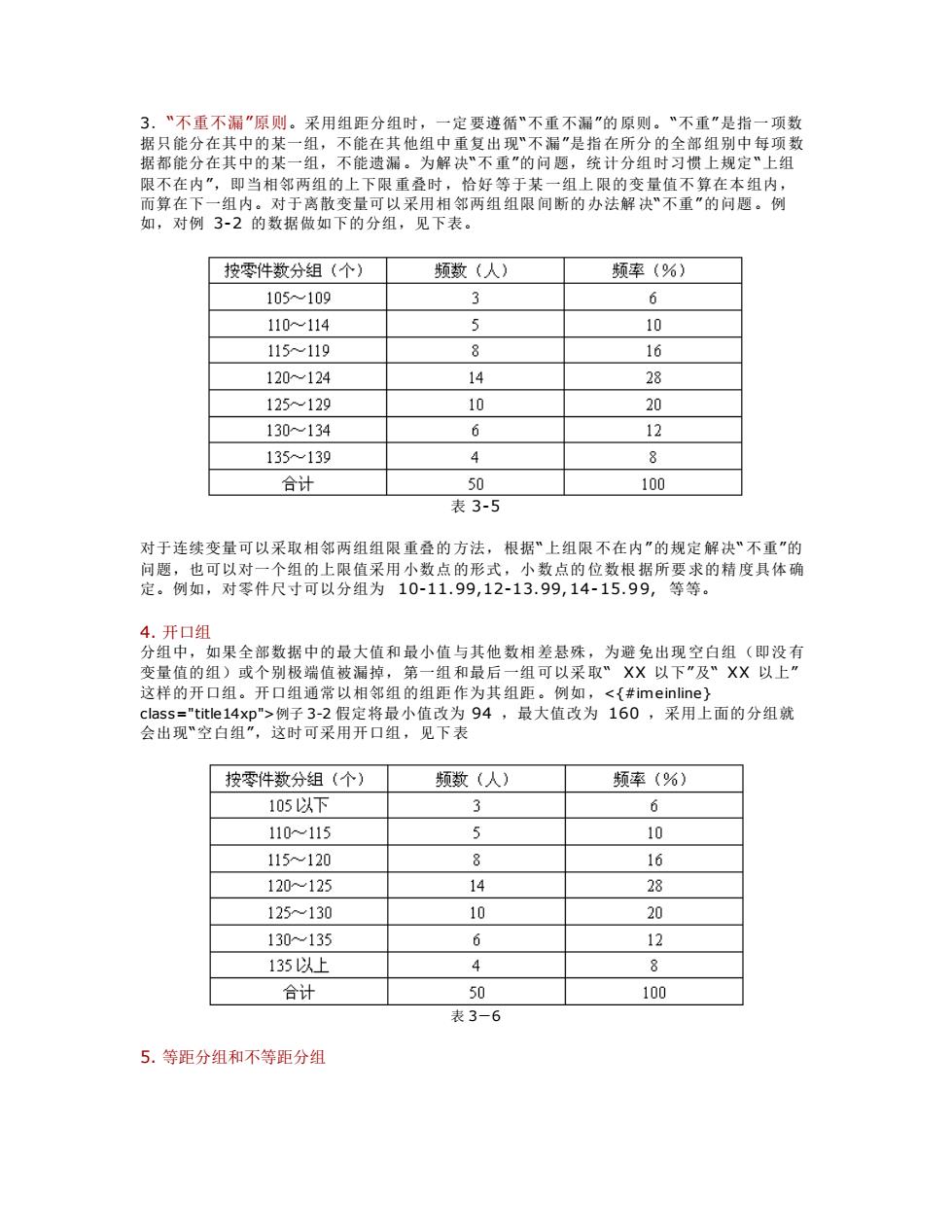
3.“不重不漏”原则。采用组距分组时,一定要遵循“不重不漏”的原则。“不重”是指一项数 据只能分在其中的某一组,不能在其他组中重复出现“不漏”是指在所分的全部组别中每项数 据都能分在其中的某一组,不能遗漏。为解决“不重”的问题,统计分组时习惯上规定“上组 限不在内”,即当相邻两组的上下限重叠时,恰好等于某一组上限的变量值不算在本组内, 而算在下一组内。对于离散变量可以采用相邻两组组限间断的办法解决“不重”的问题。例 如,对例 3-2 的数据做如下的分组,见下表。 表 3-5 对于连续变量可以采取相邻两组组限重叠的方法,根据“上组限不在内”的规定解决“不重”的 问题,也可以对一个组的上限值采用小数点的形式,小数点的位数根据所要求的精度具体确 定。例如,对零件尺寸可以分组为 10-11.99,12-13.99, 14- 15.9 9, 等等。 4. 开口组 分组中,如果全部数据中的最大值和最小值与其他数相差悬殊,为避免出现空白组(即没有 变量值的组)或个别极端值被漏掉,第一组和最后一组可以采取“ XX 以下”及“ XX 以上” 这样的开口组。开口组通常以相邻组的组距作为其组距。例如,<{#imeinline} class="title14xp">例子 3-2 假定将最小值改为 94 ,最大值改为 160 ,采用上面的分组就 会出现“空白组”,这时可采用开口组,见下表 表 3-6 5. 等距分组和不等距分组

:等分组。在组距分组如果各组的组相称为距分组,上面的几种分组 组距因素影的的 布的特 不等距分组 组频数的分 组组距不等的组距分组称为 不 对频数 布的影响 需要计算频数密度,即 员维施盖了各组内的数浆分布状况为反映各组数据的一般水平,我们道常用组中修 组中值 两侧是 一假定,用 定的 误差 二定距数据和定比数据的图示 定序数据。 <一>分组数据:直方图和折线图 折线图和曲线图等。 1直方图(Hist 。直方图是用矩形的宽度和高度来表示频数分布的图形。 平面直角坐标中,横辑表示数据分组:飘轴表示频数或频幸,这样,示各组与相应的频数就形 成了一个矩形,即直方图。例如,根据表3一4频数分布汇成的直方图如下图
• 等距分组。在组距分组时,如果各组的组距相等则称为等距分组,如上面的几种分组就是 等距分组。等距分组由于各组的组距相等,各组频数的分布不受组距大小的影响,它同消除 组距因素影响的频数密度(即单位组距内分布的特征和规律,也称次数密度)的分布是一致 的,因此可直接根据绝对频数来观察频数分布的特征和规律。 • 不等距分组。各组组距不等的组距分组称为不等距分组。不等距分组因各组组距不同,各 组频数的分布受组距大小不同的影响,因此各组绝对频数的多少并不能反映频数分布的实际 情况。为消除组距不同对频数分布的影响,需要计算频数密度,即 频率密度 = 频率 ÷ 组 距 。频数密度能准确反映频数分布的实际情况。 6. 组中值 组距分组掩盖了各组内的数据分布状况,为反映各组数据的一般水平,我们通常用组中值 ( Class midpoint )作为该组数据的一个代表值,即 组中值 = (上限 + 下限)÷ 2 。 但这种代表值有一个必要的假定条件,即各组数据在本组内呈均匀分布或在组中值两侧呈对 称分布。如果实际数据的分布不符合这一假定,用组中值作为一组数据的代表值会有一定的 误差。 二. 定距数据和定比数据的图示 第二节中介绍的条形图、圆形图、环行图及累积分布图等都适用于显示定距数据和定比数 据。此外,对定距数据和定比数据还有以下一些图示方法,这些方法并不适用于定类数据和 定序数据。 <一>分组数据:直方图和折线图 通过数据分组后形成的频数分布表,可以初步看出数据分布的一些特征和规律。如果用图形 来表示这一分布的结果,会更加形象和直观。显示分组数据频数分布特征的图形有直方图、 折线图和曲线图等。 1 .直方图( Histogram )。直方图是用矩形的宽度和高度来表示频数分布的图形。在 平面直角坐标中,横轴表示数据分组,纵轴表示频数或频率,这样,各组与相应的频数就形 成了一个矩形,即直方图。例如,根据表 3 - 4 频数分布汇成的直方图如下图