PERCENT 30 0 000000000011111111112222222222333333333344444444445 012345678901234567890123456789012345678901234567890 x MIDPOINT (a)原始数据 CENT 30 000000000011111111112222222222333333333344444444445 00000000011111111112222222222333333333344444444445 012345678901234567890123456789012345678901234567890 012345678901234567890123456789012345678901234567890 mm MIDPOINT mm MIDPOINT (b)n=5 (c)=10
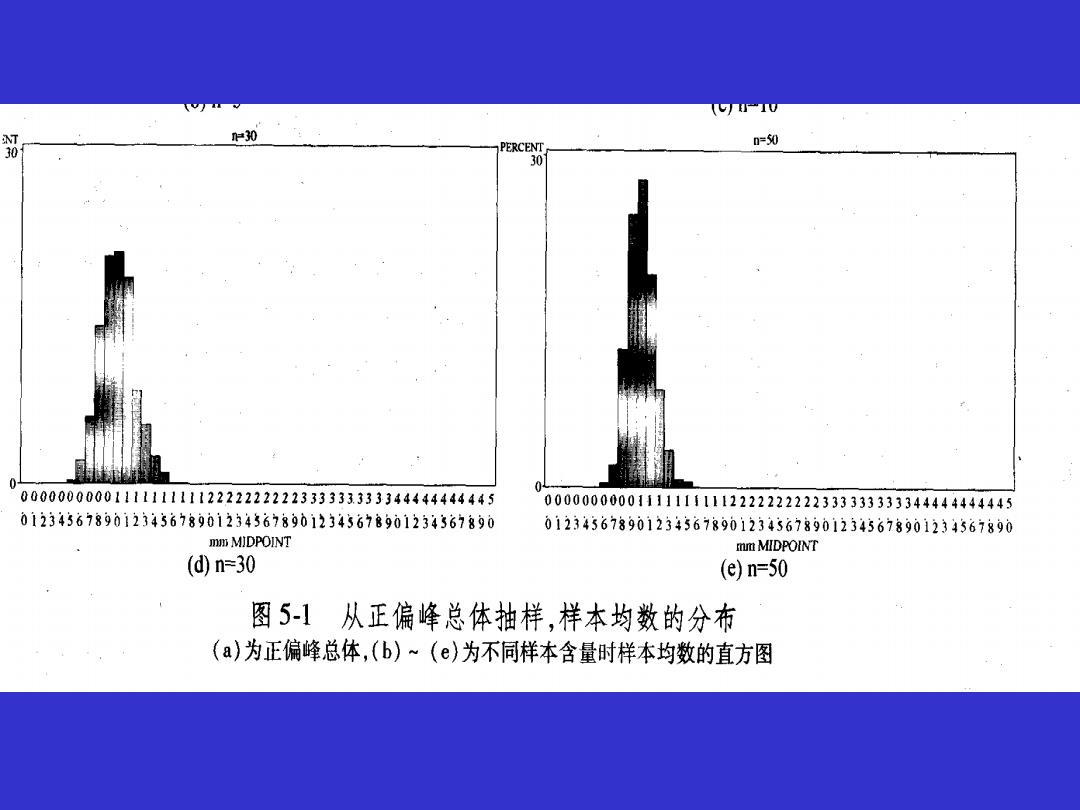
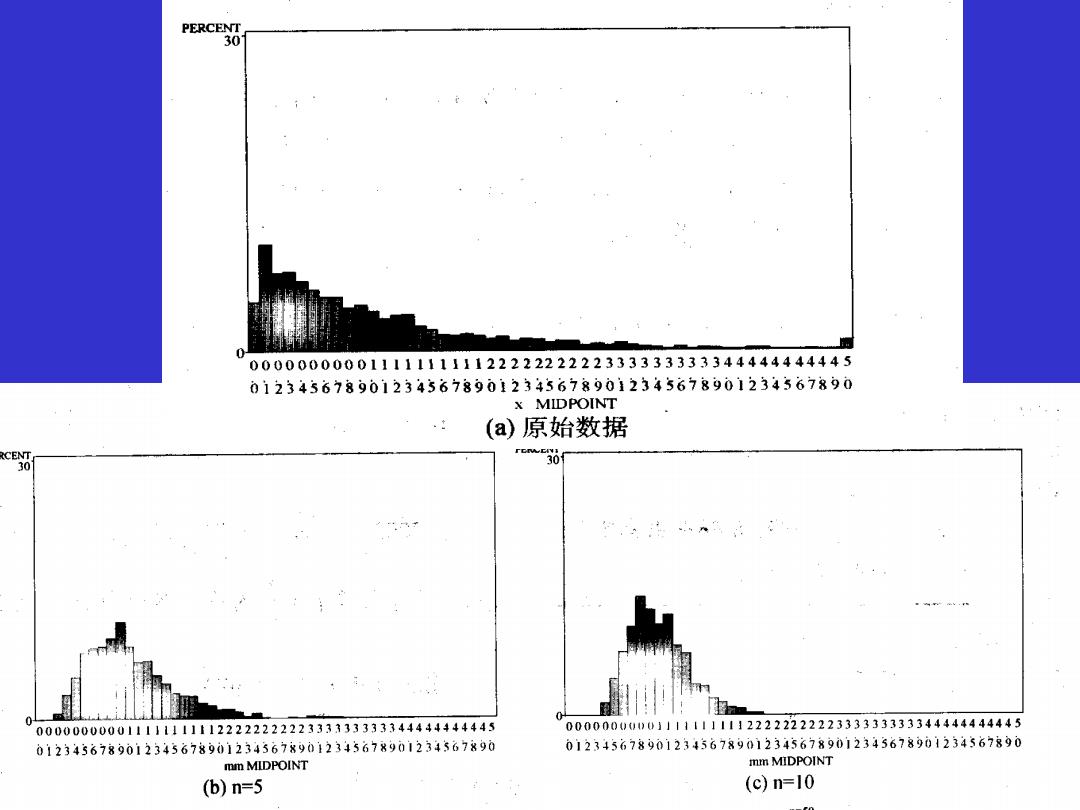
10 T 片30 PERCENT 0=50 30 0 000000000011111111112222222222333333333344444444445 00000000001111111111222222222333333333344444444445 012343678901234367890123436789012345678901234367890 012343678901234367890123436789012345678901234567890 mm MIDPOINT mm MIDPOINT (d)n=30 (e)n=50 图5-1从正偏峰总体抽样,样本均数的分布 (a)为正偏峰总体,(b)~(e)为不同样本含量时样本均数的直方图

数理统计推理和中心极限定理表明: 1)从正态总体N(μ,o)中,随机抽取例数为n的多 个样本,样本均数 服从正态分布;即使是从偏态 总体中随机抽样,当n足够大时(如n>50),x也近 似正态分布。 2)从均数为小,标准差为σ的正态或偏态总体中抽 取例数为的样本,样本均数的标准差即标准误为o。 ox =GI/n
1)从正态总体N(µ,σ2 )中,随机抽取例数为n的多 个样本,样本均数 服从正态分布;即使是从偏态 总体中随机抽样,当n足够大时(如n>50), 也近 似正态分布。 数理统计推理和中心极限定理表明: 2)从均数为µ,标准差为σ的正态或偏态总体中抽 取例数为n的样本,样本均数的标准差即标准误为 。 n X = /

表8-2100个样本均数的频数表与标准误的计算表 身高组段 频数 组中值 X fx2 152.6 1 152.9 153.2 4 153.5 153.8 4 154.1 154.4 22 154.7 155.0 25 155.3 155.6 21 155.9 156.2≈ 17 156.5 156.8 3 157.1 157.4 2 157.7 158.0 1 158.3 合计 100 ΣX2-(②X1Σf Σf-1
身高组段 频数 组中值 fX fX2 152.6~ 1 152.9 153.2~ 4 153.5 153.8~ 4 154.1 154.4~ 22 154.7 155.0~ 25 155.3 155.6~ 21 155.9 156.2~ 17 156.5 156.8 ~ 3 157.1 157.4 ~ 2 157.7 158.0 ~ 1 158.3 合计 100 表8-2 100个样本均数的频数表与标准误的计算表

0x=o/√n (标准误的理论值) 标准误的大小与o的大小成正比,与成反比,而 σ为定值,说明可以通过增加样本例数来减少标准误, 以降低抽样误差。 σ未知,用样本标准差$来估计总体标准差·。 Sx =SIVn (标准误的估计值) 用Sx来表示均数抽样误差的大小
标准误的大小与σ的大小成正比,与n成反比,而 σ为定值,说明可以通过增加样本例数来减少标准误, 以降低抽样误差。 σ未知,用样本标准差S来估计总体标准差σ。 用 来表示均数抽样误差的大小。 S S n X = / (标准误的理论值) (标准误的估计值)