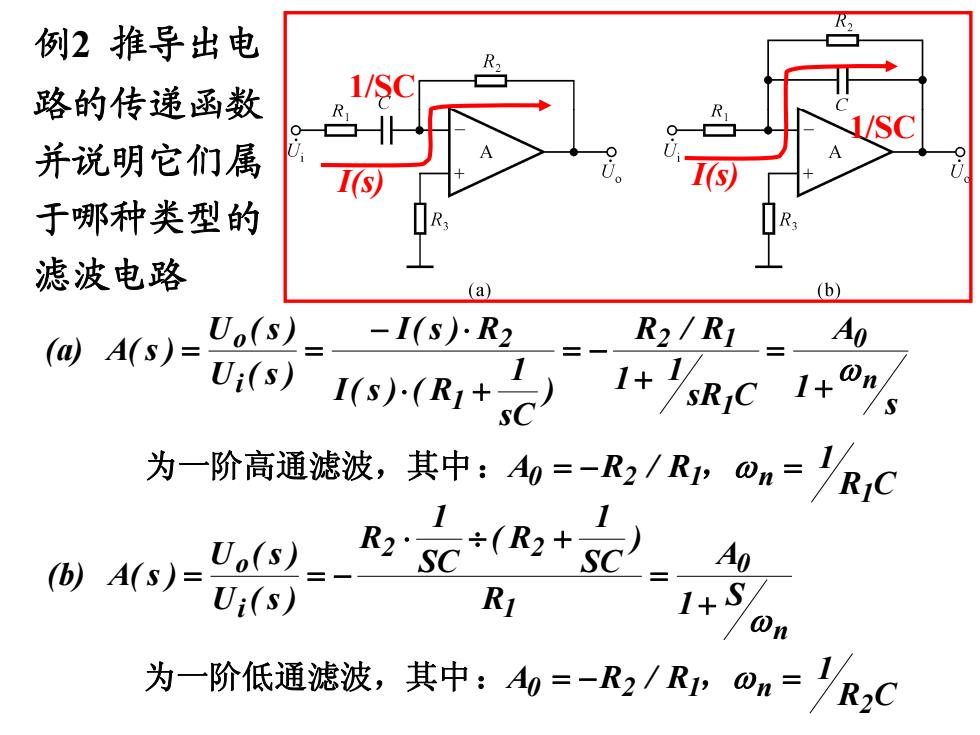
例2推导出电 路的传递函数 1/SC 并说明它们属 I(s) 于哪种类型的 滤波电路 (a) (b ()A(s)= U(s=-I(s小R2 =-R2/R1=A0 Ui(s) 1-风+1+R,e1+。 为一阶高通滤波,其中:=-R/R,@n=R,C (b)A(s)= U:(s) R 1+ /On 为一阶低通滤波,其中:=-R/Rn@u=发,C
例2 推导出电 路的传递函数 并说明它们属 于哪种类型的 滤波电路 s 1 A CsR 1 1 R/R ) sC 1 R()s(I R)s(I )s(U )s(U )s(A (a) n 0 1 12 1 2 i o CR R/RA 1 1 为一阶高通滤波,其中: , n120 1/SC 1/SC I(s) I(s) n 0 1 2 2 i o S 1 A R ) SC1 R( SC1 R )s(U )s(U )s(A (b) CR R/RA 1 2 为一阶低通滤波,其中: ,n120
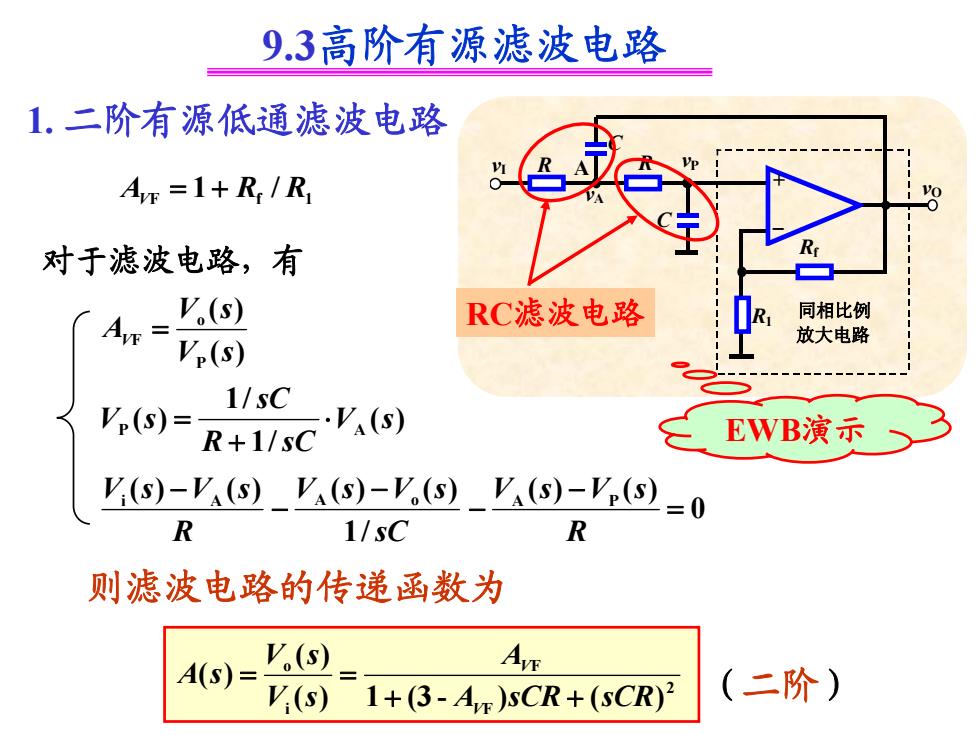
9.3高阶有源滤波电路 1.二阶有源低通滤波电路 AvE=1+R/R 对于滤波电路,有 Aw= s) RC滤波电路 同相比例 放大电路 p(s) 1/sC V(s)= R+1/sC .V(s) EWB演示 ys)-ys_V)-_',)-=0 R 1/sC R 则滤波电路的传递函数为 A(S)= V(s) AvE '(s) 1+(3-Arg)sCR+(sCR)2 (二阶)
1. 二阶有源低通滤波电路 F 1f V /1 RRA )( )( P o F sV sV AV )( /1/1 )( P A sV sCR sC sV vI Rf – + vP R1 放大电路 同相比例 vO vI Rf C – + vP R1 放大电路 同相比例 R vO vI C Rf R C – + vP R1 放大电路 同相比例 vA A R vO vI C Rf R C – + vP R1 放大电路 同相比例 vA A R vO 对于滤波电路,有 R sVsV )()(i A sC sVsV /1 )()( A o 则滤波电路的传递函数为 )( )( )( i o sV sV sA 2 F F sCRsCRA )()-(31 A V V (二阶) 9.3高阶有源滤波电路 0 )()( A P R sVsV RC滤波电路 EWB演示

V,(s) A(S)= Ar V(s) 1+(3-AvE)sCR+(SCR)2 Av =1+R/R 令 A0=AvF 称为通带增益 1 nRC 称为特征角频率 1 0= 3-AvF 称为等效品质因数 则 A(S)= Ay@听 52 0ns+ωn 2 注意:当3-A>0,即Ap<3时,滤波电路才能稳定工作
令 A AV0 F 称为通带增益 RC 1 n 称为特征角频率 A3 VF 1 Q 称为等效品质因数 则 2 n 2 n 2 n0 s Q s A )s(A 注意: 当3-AVF >0, 即AVF <3时, 滤波电路才能稳定工作. )( )( )( i o sV sV sA 2 F F sCRsCRA )()-(31 A V V F 1f V /1 RRA

A@7 Ao A(S)= s=jw A(j0) 52+ ns+On 频率响应 1-(2+ian ◆归一化的幅频响应 20 1g Ao 12 @,O ◆相频响应 (@)=-arctg 1- 02
2 n 2 n 2 n0 s Q s A )s(A ) Q (j)(1 A )j(A n 2 n 0 s j 频率响应 2 n 2 2 n 0 ) Q ()(1 1 lg20 A )j(A lg20 ◆归一化的幅频响应 ◆相频响应 2 n n )(1 Q arctg)(
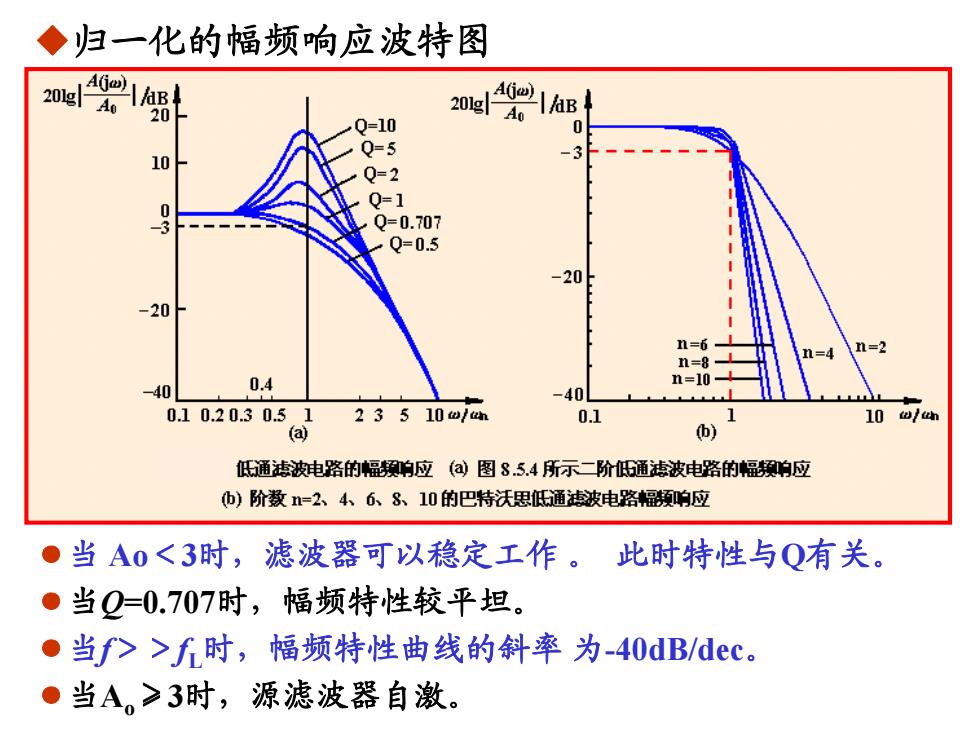
◆归一化的幅频响应波特图 20 Q-10 2e21。 Q=5 10 3 Q=2 0 Q=1 -3 Q=0.707 Q=0.5 -20 -20 n=6 n=8 -40 0.4 n=10- -40 0.10.20.30.51 23510u1m 0.1 10/h (a ) 低通滤波纯路的响应(a图8.5.4所示一阶6通滤波电路的响应 b)阶数=2、4、6、8、10的巴特沃思低通波电路频响应 ●当A0<3时,滤波器可以稳定工作。此时特性与Q有关。 ●当Q=0.707时,幅频特性较平坦。 ●当f>>f时,幅频特性曲线的斜率为-40dB/dec. ●当A。≥3时,源滤波器自激
◆归一化的幅频响应波特图 ●当 Ao<3时,滤波器可以稳定工作 。 此时特性与Q有关。 ●当Q=0.707时,幅频特性较平坦。 ●当f>>fL时,幅频特性曲线的斜率 为-40dB/dec。 ●当Ao≥3时,源滤波器自激