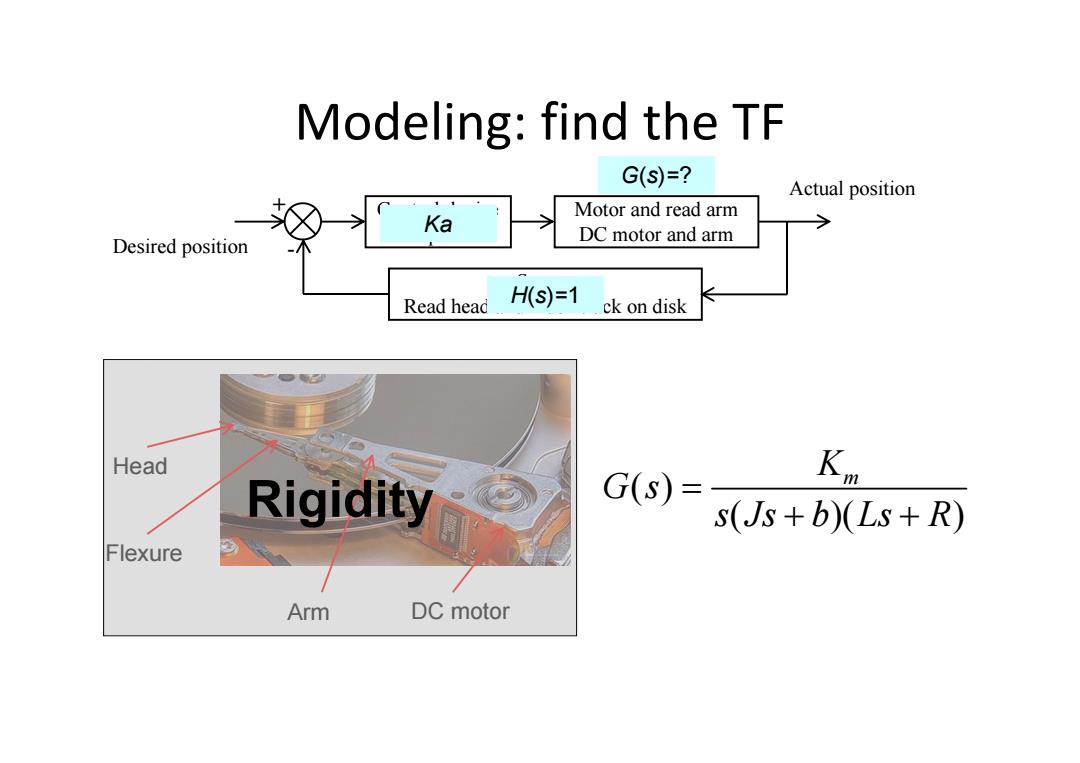
Modeling:find the TF G(S)=? Actual position Motor and read arm Ka Desired position DC motor and arm Read head HS)=1 ck on disk Head G(s) Kn Rigidity s(Js+b)(Ls+R) Flexure Arm DC motor
Modeling: find the TF Control device Amplifier Motor and read arm DC motor and arm Sensor Read head and index track on disk Desired position Actual position + - Ka H(s)=1 G(s)=? Arm DC motor Flexure Head Rigidity ( ) ( )( ) Km G s s Js b Ls R
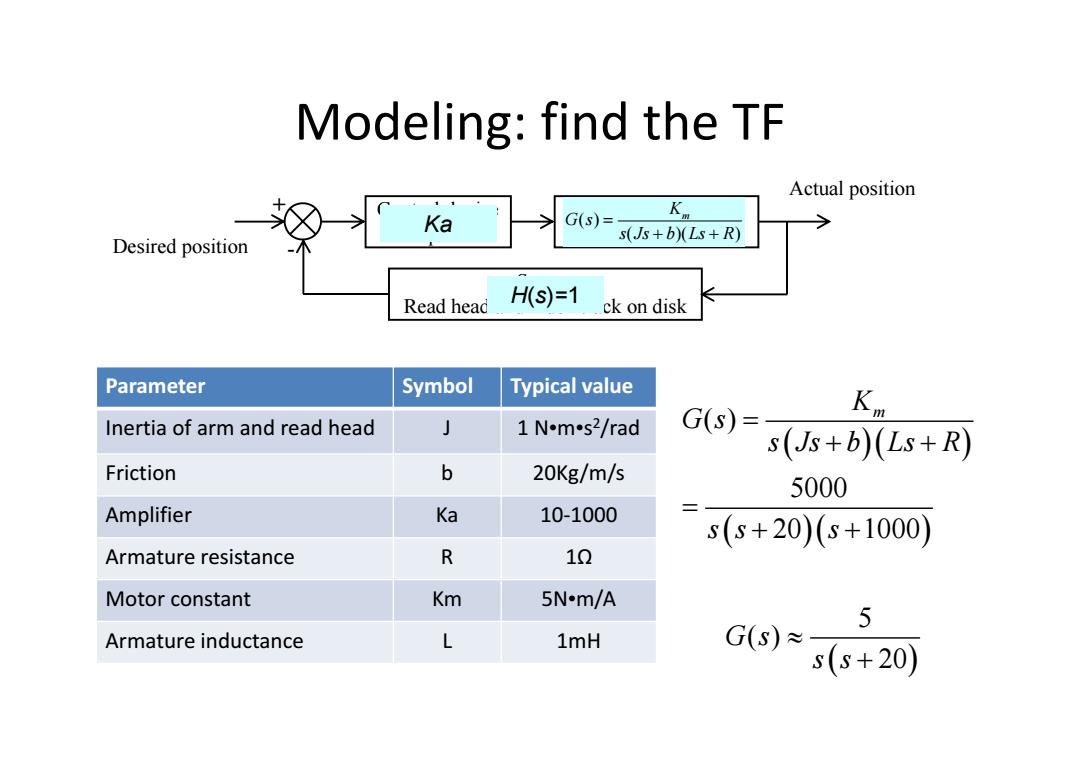
Modeling:find the TF Actual position Ka G(s)= s(Js+b)(Ls+R) Desired position Read head HS)=1 ck on disk Parameter Symbol Typical value Inertia of arm and read head 1 N.m-s2/rad G(s)= (Js+b)(Ls+R) Friction b 20Kg/m/s 5000 Amplifier Ka 10-1000 s(s+20)(s+1000) Armature resistance R 10 Motor constant Km 5N-m/A 5 Armature inductance L 1mH G(s)≈ s(s+20)
Modeling: find the TF Control device Amplifier Motor and read arm DC motor and arm Sensor Read head and index track on disk Desired position Actual position + - Ka H(s)=1 ( ) ( )( ) Km G s s Js b Ls R Parameter Symbol Typical value Inertia of arm and read head J 1 N•m•s2/rad Friction b 20Kg/m/s Amplifier Ka 10‐1000 Armature resistance R 1Ω Motor constant Km 5N•m/A Armature inductance L 1mH ( ) 5000 20 1000 K m G s s Js b Ls R ss s 5 ( ) 20 G s s s
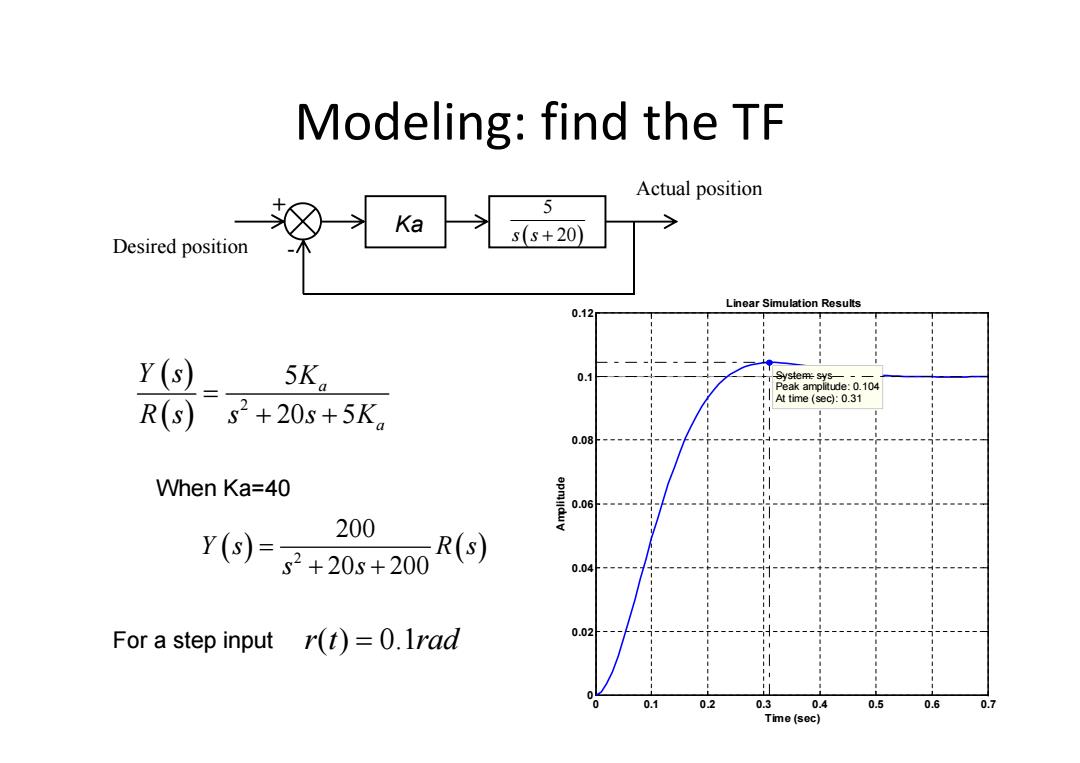
Modeling:find the TF Actual position 5 Ka Desired position s(s+20) Linear Simulation Results 0.12 Y(s) 5Ka 0.1 yeys Peak amolitude:0.104 2+20s+5K。 At time (sec):0.31 R(s)5 0.08 When Ka=40 0.06 200 Y()=子+20s+200 R(s) 0.04 For a step input r(t)=0.1rad 0.02 0.1 0.2 0.3 0.4 0.5 0.6 0.7 Time (sec)
Modeling: find the TF Desired position Actual position + - 5 s s 20 Ka 2 5 20 5 a a Y s K R s s sK When Ka=40 2 200 20 200 Y s Rs s s For a step input r t rad ( ) 0.1 Linear Simulation Results Time (sec) Amplitude 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0 0.02 0.04 0.06 0.08 0.1 0.12 System: sys Peak amplitude: 0.104 At time (sec): 0.31
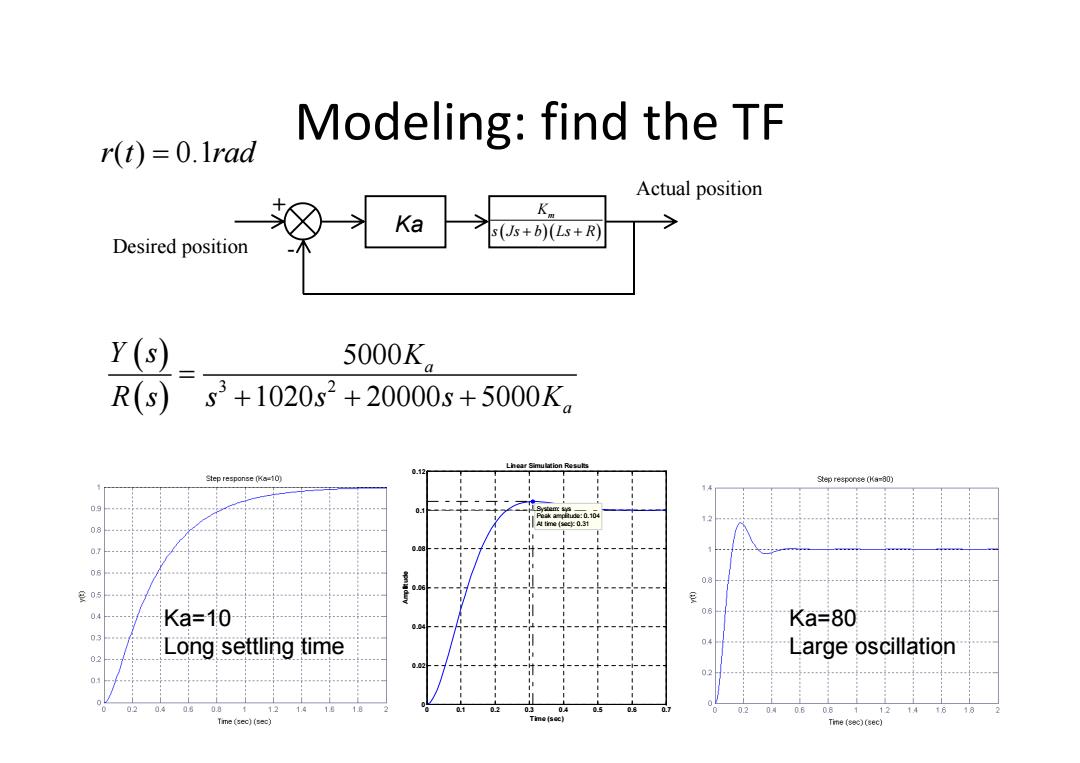
Modeling:find the TF r(t)=0.Irad Actual position Ka Ka s(Js+b)(Ls+R) Desired position Y(s) 5000K R(s) s3+1020s2+20000s+5000K, 212 Step response (Ka-10) Step response (Ka-80) 0.10 0.3 皇05 Ka=10 Ka=80 Long settling time Large oscillation 04 06 06 12 Tme (sec)(sec) Time(sec)(sec)
Modeling: find the TF r t rad ( ) 0.1 Desired position Actual position + - Ka Km s Js b Ls R 3 2 5000 1020 20000 5000 a a Y s K Rs s s s K Linear Simulation Results Time (sec) Amplitude 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0 0.02 0.04 0.06 0.08 0.1 0.12 System: sys Peak amplitude: 0.104 At time (sec): 0.31 Ka=10 Long settling time Ka=80 Large oscillation