西安电子科技大学：《电路分析基础》课程教学课件（讲稿）第五章 电路频率响应和谐振现象

5.2一阶电路苑二阶电路的频率响店 一阶电路和二阶电路是常用的两类重要电路。它通常是 构成高阶电路的基本单元模块。 一、一阶电路 一阶电路按频率响应可分为：低通、高通和全通三种类型， 其网络函数的典型形式为 低通函数 H(jo)=Ho j0+0c 高通函数 H(jo)=H J0 j0+0c 全通函数 H(Uo)=H。 J0-0e j0+0c

西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 一阶电路和二阶电路是常用的两类重要电路。它通常是 构成高阶电路的基本单元模块。 一、一阶电路 一阶电路按频率响应可分为：低通、高通和全通三种类型， 其网络函数的典型形式为 C C j H j H       0 低通函数 ( ) C j H j H        j 高通函数 ( ) C C j H j H         j ( ) 全通函数 0 第 5-11 页 前一页 下一页 退出本章

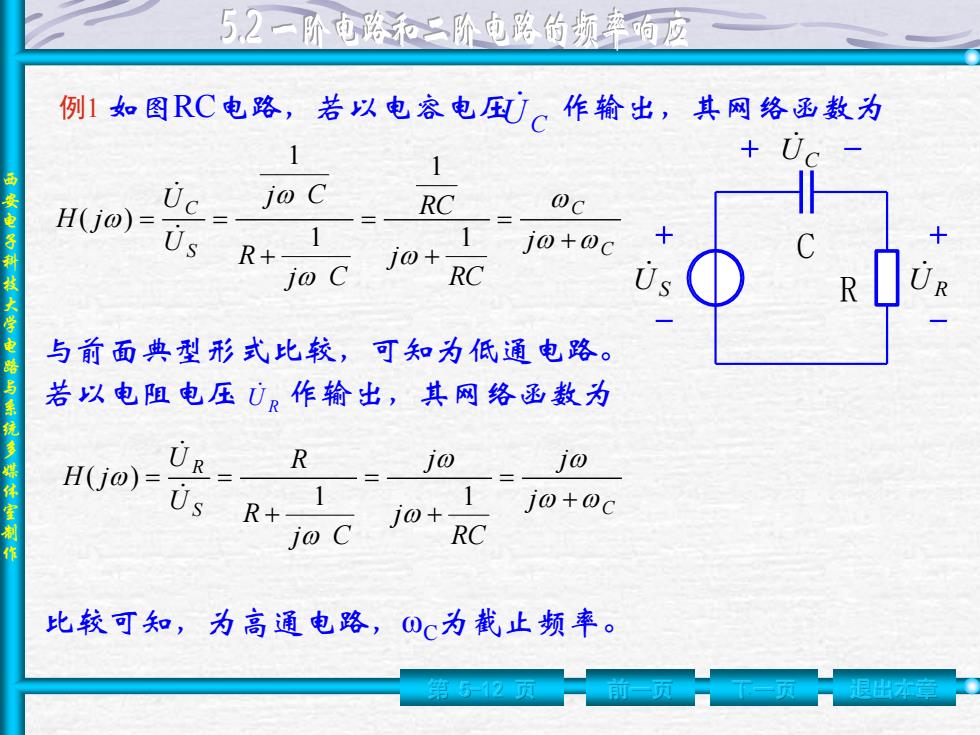
52一阶路和二阶电路的频率响应 例1如图RC电路，若以电容电。作输出，其网络函数为 1 1 H(jo)= Uc jo C RC @c Us 1 R+ J0+ 1j0+0c jo C RC S 与前面典型形式比较，可知为低通电路。 若以电阻电压0。作输出，其网络函数为 H(j0)= UR R jo jo Us R+- 1 j0+0c jo C j0+ RC 比较可知，为高通电路，Oc为截止频率

西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 5-12 页 前一页 下一页 退出本章 C S R U UC  UR  UC  C C S C j RC j RC j C R j C U U H j               1 1 1 1 ( )   与前面典型形式比较，可知为低通电路。 若以电阻电压 U  R 作输出，其网络函数为 S C R j j RC j j j C R R U U H j               1 1 ( )   比较可知，为高通电路，ωC为截止频率。 例1 如图RC电路，若以电容电压 作输出，其网络函数为

5,2一阶中衣阶电路的频的方 二、二阶电路 二阶电路按频率响应可分为：低通、高通、带通、 带阻和全通五种类型，其网络函数的典型形式为 低通函数 带阻函数 H(jo)=H (joP+@p H(jo)=Ho jo}+ o(jw)+@i 0o}+Uo)+d 高通函数 全通函数 H(jo)=H, (j@P (joP-@(jo)+o (o 2+ 0o(jo)+0 H(jo)=Ho 带通函数 (joY+(jo)+0j 0(jo) H(jo)=H。 (joY+(jo)+o

西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 5-13 页 前一页 下一页 退出本章 二阶电路按频率响应可分为：低通、高通、带通、 带阻和全通五种类型，其网络函数的典型形式为   2 0 0 2 2 0 0 ( ) ( )          j Q j H j H 低通函数   2 0 0 2 2 ( ) j ( )           j Q j H j H （ ） 高通函数   2 0 0 2 0 0 ( ) j ( )           j Q j Q H j H （ ） 带通函数   2 0 0 2 2 0 2 ( ) j ( )             j Q j H j H （ ） 带阻函数   2 0 0 2 2 0 2 0 0 ( ) j ( ) ( )               j Q j j Q H j H （ ） 全通函数 二、二阶电路

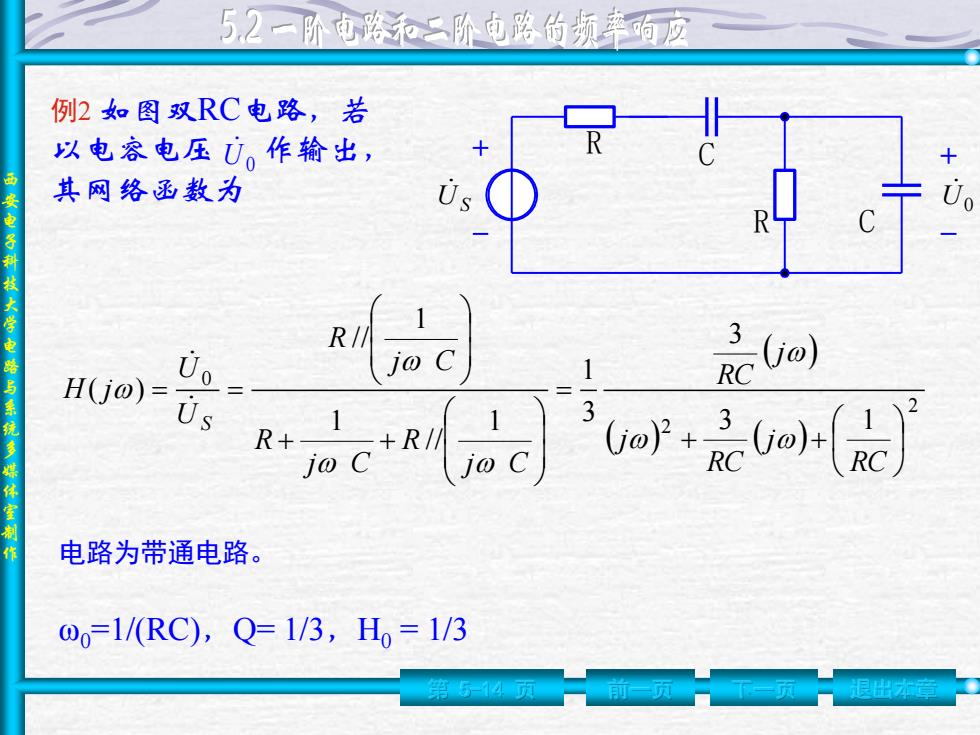
5,2一阶中路二阶屯路的频率的应 例2如图双RC电路，若 以电容电压U。作输出， 其网络函数为 jo C H(j) Us R* ae) 3 +RI∥ jo C (oFc(e) 电路为带通电路。 o0=1/RC),Q=1/3,H=1/3

西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 例2 如图双RC电路，若 以电容电压 作输出， 其网络函数为 第 5-14 页 前一页 下一页 退出本章 U 0  C R US  R C U0        2 2 0 3 1 3 3 1 1 / / 1 1 / / ( )                              RC j RC j j RC j C R j C R j C R U U H j S          电路为带通电路。 ω0=1/(RC)，Q= 1/3，H0 = 1/3

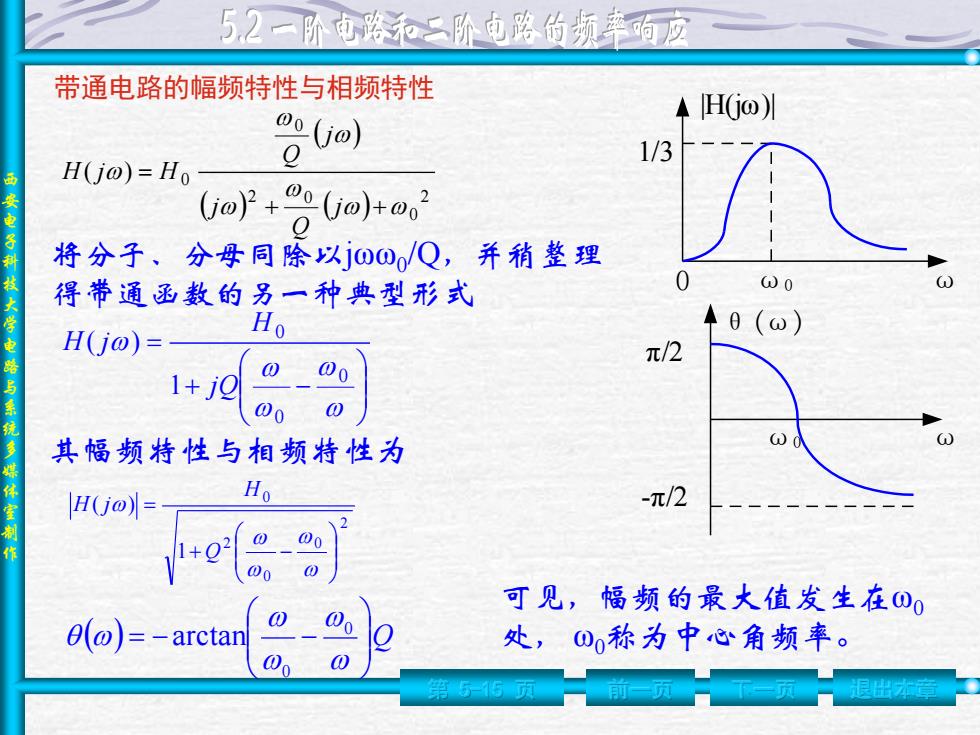
5,2一阶电二阶屯路的频率的应 带通电路的幅频特性与相频特性 ◆H(Go)川 o(jo) 1/3 H(j@)=Ho (oY+0(0)+0 将分子、分母同除以jO0/Q,并稍整理 得带通函数的另一种典型形式 0 ⊙0 H(jo)= Ho ◆0（ω） π/2 1+j0 000 000 其幅频特性与相频特性为 G)d H(j@)= Ho -π/2 1+02 000 可见，幅频的最大值发生在O0 θo)=-arctan 000 处，0称为中心角频率

西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 5-15 页 前一页 下一页 退出本章       2 0 2 0 0 0 ( )           j Q j j Q H j H 将分子、分母同除以jωω0 /Q，并稍整理 得带通函数的另一种典型形式                 0 0 0 1 ( ) jQ H H j 其幅频特性与相频特性为 2 0 0 2 0 1 ( )                 Q H H j   Q                 0 0 arctan 带通电路的幅频特性与相频特性 0 ω0 ω 1/3 |H(jω)| ω0 ω θ(ω) π/2 -π/2 可见，幅频的最大值发生在ω0 处， ω0称为中心角频率