第五章电路频率响应和脂振现象 对前面的低通电路,由H(j而) 于Hmax=1,故由 H max V1+(@cCR) -0707= 解得:oc=1/RC)。 4HGo)川 HGo)儿 按通带、止带来分类,可分 为:低通(a)、高通(b)、带通(c)小 通带 止带 止带 通带 带阻(d)和全通()滤波电路。其 幅频特性分别为 0 Wc 00 Wc 0 (a) (b) H(jo川 H(Gj@川 H(j) 止带通带 止带 通带 止带通带 通带 0C1 0C2 0 0 @CI 0C20 (e) (c) (d)
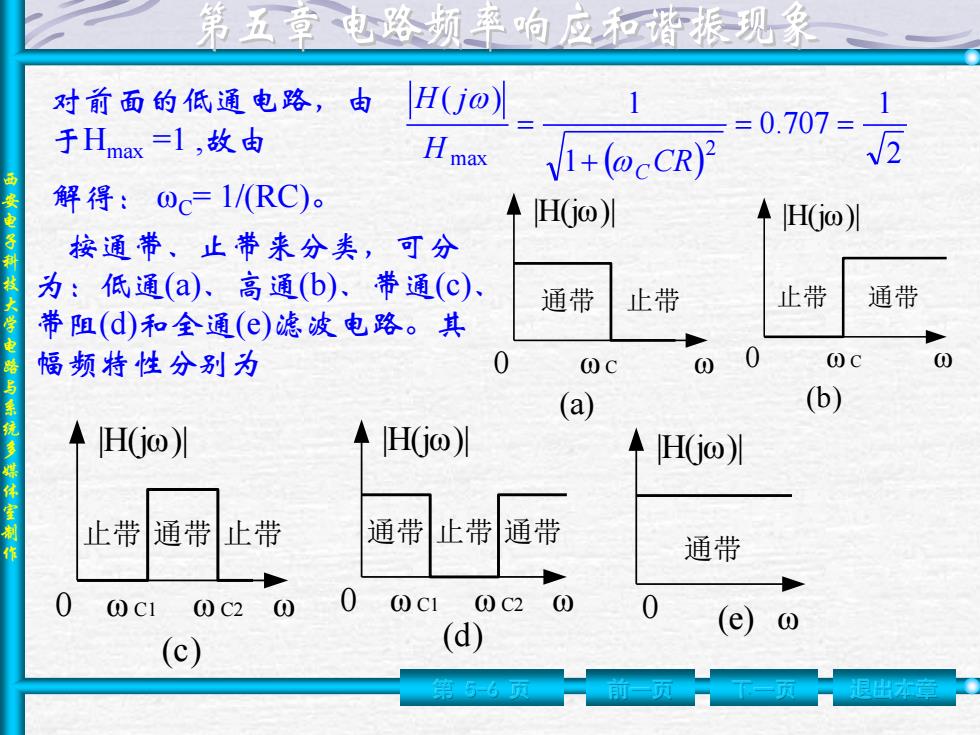
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 5-6 页 前一页 下一页 退出本章 2 1 0.707 1 ( ) 1 2 max CR H H j C 解得: ωC= 1/(RC)。 按通带、止带来分类,可分 为:低通(a)、高通(b)、带通(c)、 带阻(d)和全通(e)滤波电路。其 幅频特性分别为 0 ω C ω (a) |H(jω)| 通带 止带 0 ω C ω (b) |H(jω)| 止带 通带 0 ω C1 ω (c) |H(jω)| 止带 通带 止带 ω C2 0 ω C1 ω (d) |H(jω)| 通带 止带 通带 ω C2 0 (e) ω |H(jω)| 通带 对前面的低通电路,由 于Hmax =1 ,故由
第五章电路频率响应和谐派现象 例2如图正孩稳态电路,R=1k2,C=1uF,o=103rad/s 当s()=10+10cos(ot)+10cos(2oot)+10cos(3ot)V时,电压 c(t)=? 解根据叠加定理,响应u()看作s()的四 个分量分别作用的结果。网络函数为 Us 1 jo C H(jo)= 0c Us 1+j@CR 1+j0x10-3 对于不同频率,HGO)的值分别为 HG0)=1, HGo0)=0.707∠-45°, H020)=0.447∠-63.4°, HG3o)=0.316∠-71.6°
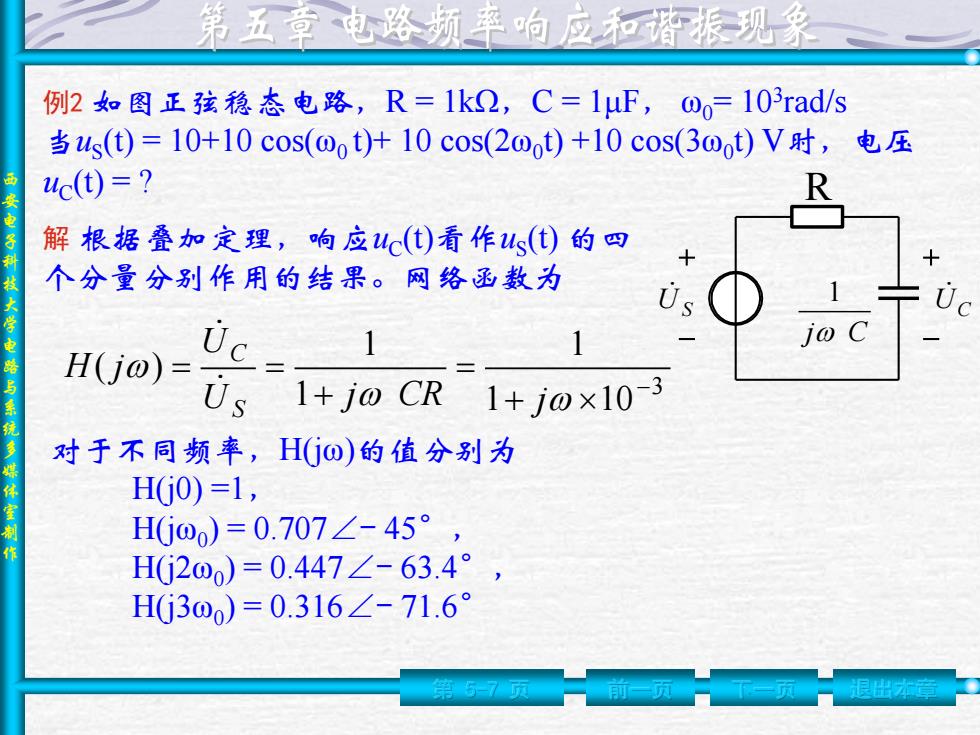
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 5-7 页 前一页 下一页 退出本章 U S UC R j C 1 例2 如图正弦稳态电路,R = 1kΩ,C = 1μF, ω0= 103 rad/s 当uS (t) = 10+10 cos(ω0 t)+ 10 cos(2ω0 t) +10 cos(3ω0 t) V时,电压 uC (t) = ? 解 根据叠加定理,响应uC (t)看作uS (t) 的四 个分量分别作用的结果。网络函数为 3 1 10 1 1 1 ( ) U j CR j U H j S C 对于不同频率,H(jω)的值分别为 H(j0) =1, H(jω0 ) = 0.707∠- 45° , H(j2ω0 ) = 0.447∠- 63.4° , H(j3ω0 ) = 0.316∠- 71.6°

第五章电路频率响应扣谐振现象 考虑到输入相量(对应不同频率): Usm (0)=Usm (@o)=Usm(200)=Usm (300)=1020V 故对应各频率的响应相量分别为 Ucm(0)=H(0)Um(0)=10∠0V, U。m(oo)=H(j0)Usm(0o)=7.07∠-45V Ucm(20o)=H(j20o)Usm(20o)=4.47∠-63.4V, Ucm(3o)=H(Uj30)0sm(3w)=3.16∠-71.6V .uc(t)=10+7.07c0s(0t-45)+4.47c0s(20ot-63.4) +3.16cos(30t-71.6)/ 可见,电路的网络函数是联系输入和输出的纽带。反映了响应随频率变化 的情况
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 5-8 页 前一页 下一页 退出本章 U S m (0) U S m ( 0 ) U S m (2 0 ) U S m (3 0 ) 1 00V 故对应各频率的响应相量分别为 U (0) H ( j0)U (0) 10 0 V , Cm Sm (2 ) ( 2 ) (2 ) 4.47 63.4 , U Cm 0 H j 0 U Sm 0 V t V u t t t C 3.16cos(3 71.6) ( ) 10 7.07 cos( 45 ) 4.47 cos(2 63.4 ) 0 0 0 可见,电路的网络函数是联系输入和输出的纽带。反映了响应随频率变化 的情况。 考虑到输入相量(对应不同频率): U Cm (0 ) H( j0 )U S m (0 ) 7.07 45V U Cm (30 ) H( j30 )U S m (30 ) 3.16 71.6V
第五章电路频率响应和谐振现象 *二、波特图的概念 在电子、通信、自动控制等系统的分析和设计中,常常由 于工作频率很宽而不便画出幅频特性曲线,可以将频率特性 的纵、横坐标采用对数刻度。其优点是特性曲线可以用折线 近似,而且可以在很宽的频率范围内较完整地画出曲线。这 种用对数坐标画出的幅频和相频特性称为波特图(Bode图)。 工程上,幅频特性取对数后以分贝(B)作单位,称为增益, 用G表示。 G=20l0g10H(jo)dB [H(j@)l 0.01 0.1 0.707 1 10 100 1000 G(dB) -40 -20 -3 20 40 60
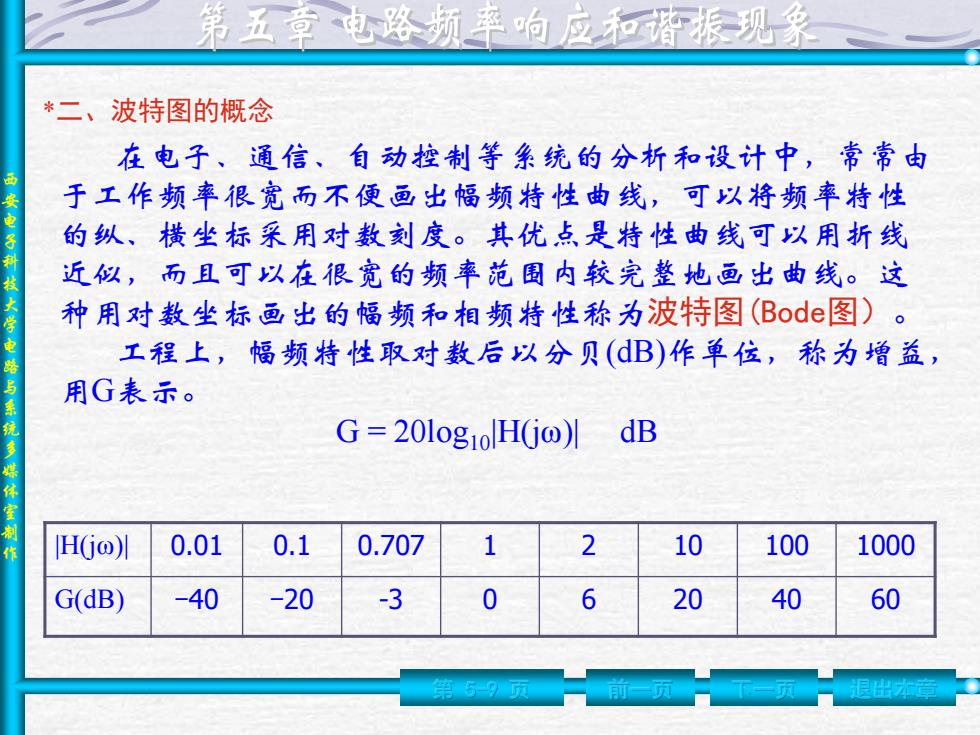
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 5-9 页 前一页 下一页 退出本章 *二、波特图的概念 在电子、通信、自动控制等系统的分析和设计中,常常由 于工作频率很宽而不便画出幅频特性曲线,可以将频率特性 的纵、横坐标采用对数刻度。其优点是特性曲线可以用折线 近似,而且可以在很宽的频率范围内较完整地画出曲线。这 种用对数坐标画出的幅频和相频特性称为波特图(Bode图)。 工程上,幅频特性取对数后以分贝(dB)作单位,称为增益, 用G表示。 G = 20log10|H(jω)| dB |H(jω)| 0.01 0.1 0.707 1 2 10 100 1000 G(dB) -40 -20 -3 0 6 20 40 60
第五章电路频率响应和谐振现象 如RC低通电路,将oc=1/(RC)代入 G=-10lg[1+(o/oc)2] 当0/@c<0.1,G0dB o 当0=0c,G=-3dB; 当o/oc>10,G≈-20lg(o/oc)。 0=10oc,G=-20dB G/dB 0 -10 -20 -30 40 -50 O/①C -60 0.0010.010.11 101001000
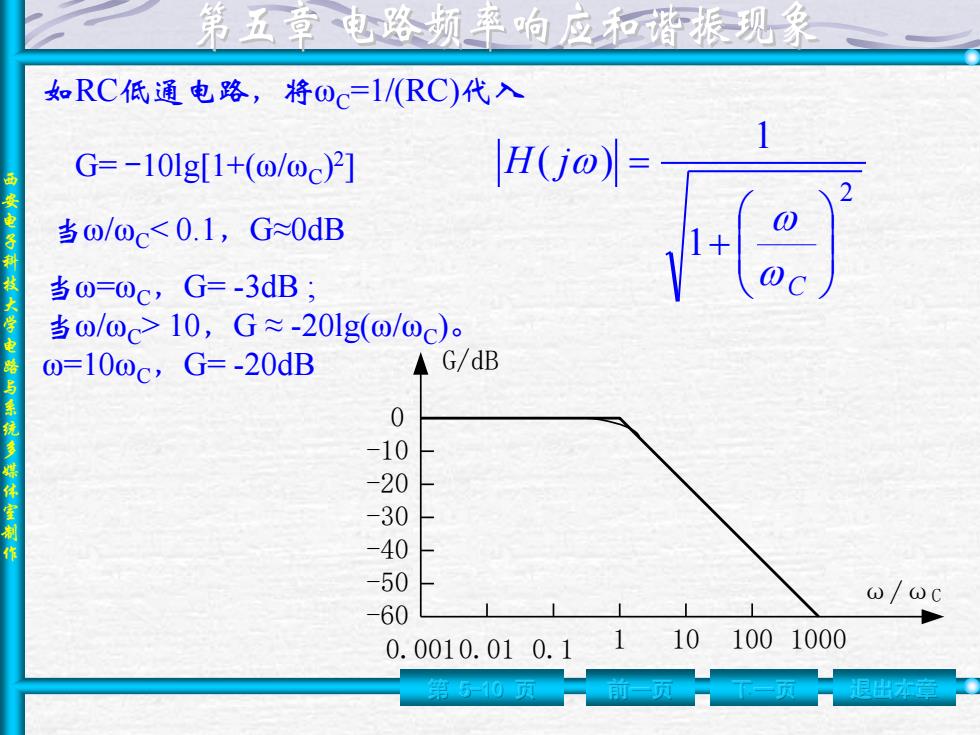
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 5-10 页 前一页 下一页 退出本章 0 -10 -20 -30 -40 -50 -60 0.0010.01 0.1 1 10 100 1000 G/dB ω/ωC 2 1 1 ( ) C H j G= -10lg[1+(ω/ωC ) 2 ] 当ω/ωC< 0.1,G≈0dB 当ω=ωC,G= -3dB ; 当ω/ωC> 10,G ≈ -20lg(ω/ωC )。 ω=10ωC,G= -20dB 如RC低通电路,将ωC=1/(RC)代入