
LLL 3a1,,am∈[0,1)s.t. cond.: Vi, Pr[A1≤a,(I-a) A,∈T(A) H:Pr[A1不A≤a holds for all smaller Say AjAjr(A),AA(A) )(U≥1 or else trivial) Pr Pr AAA AA ai ≤ neighbors non-neighbors Pr瓦…A1Ai4,…A ■≤rA1A…=PrA≤aΠ- (LLL cond.) A∈T(A) HW≥Π(-a)≥Ⅱ1- A∈T(A)
LLL cond.: ∃α s.t. 1,…, αm ∈ [0,1) ∀i, Pr[Ai ] ≤ αi ∏ Aj ∈Γ(Ai ) (1 − αj ) I.H.: Say A , j1 ,…, Ajl ∈ Γ(Ai ) Ajl+1 , …, Ajk ∉ Γ(Ai ) = Pr [AiAj1 ⋯Ajl ∣ Ajl+1 ⋯Ajk] Pr [Aj1 ⋯Ajl ∣ Ajl+1 ⋯Ajk] ≤ Pr [Ai ∣ Ajl+1 ⋯Ajk]= Pr[Ai] ≤ αi ∏ Aj ∈Γ(Ai ) (1 − αj ) (LLL cond.) Pr [Ai ∣ Aj1 ⋯Ajk] ≤ αi Pr [Ai ∣ Aj1 ⋯Ajl Ajl+1 ⋯Ajk] = l ∏ r=1 Pr [Ajr ∣ Ajr+1 ⋯Ajk] holds for all smaller k = l ∏ r=1 (1 − Pr [Ajr ∣ Ajr+1 ⋯Ajk]) ≥ l ∏ r=1 (1 − αjr) ≥ ∏ Aj ∈Γ(Ai ) (1 − αj (I.H.) ) ≤ αi (l ≥ 1 or else trivial) neighbors non-neighbors

A1,...,A has a dependency graph given by neighborhoods I() Lovasz Local Lemma (asymmetric case): 2An--公ia-心 341,,am∈[0,1): A∈T(A) chain rule [np-l m Induction Hypothesis(I.H.): istinet,AA发Pr≤a
• A has a dependency graph given by neighborhoods 1, …, Am Γ( ⋅ ) Pr [ m ⋀ i=1 Ai ] = m ∏ i=1 Pr Ai ⋀ j<i Aj = m ∏ i=1 1 − Pr Ai ⋀ j<i Aj Induction Hypothesis (I.H.): chain rule ≥ m ∏ i=1 (1 − αi ) Lovász Local Lemma (asymmetric case): ⟹ Pr [ m ⋀ i=1 Ai ] ≥ m ∏ i=1 (1 − αi ) ∃α : 1, …, αm ∈ [0,1) ∀i, Pr[Ai ] ≤ αi ∏ Aj ∈Γ(Ai ) (1 − αj ) Pr [Ai ∣ Aj1 ⋯Ajk] ≤ αi ∀ distinct A : i , Aj1 , Aj2 , …, Ajk

Lovasz Local Lemma (LLL) A1,...,A has a dependency graph given by neighborhoods I() Lovasz Local Lemma (asymmetric case): 3a1,,am∈[0,1): 元w几a-区 A∈TA) 1 01=·=Cm三 d+1 a41=…=m= 2d symmetric case: p≌max;Pr[A] d max;r(i) }n 4pd≤1
Lovász Local Lemma (LLL) • A has a dependency graph given by neighborhoods 1, …, Am Γ( ⋅ ) p ≜ max i Pr[Ai ] d ≜ maxi |Γ(i)| symmetric case: ⟹ Pr [ m ⋀ i=1 Ai ] > 0 } Lovász Local Lemma (asymmetric case): ⟹ Pr [ m ⋀ i=1 Ai ] > 0 ∃α : 1,…, αm ∈ [0,1) ∀i, Pr[Ai ] ≤ αi ∏ Aj ∈Γ(Ai ) (1 − αj ) or ep(d + 1) ≤ 1 4pd ≤ 1 α1 = ⋯ = αm = 1 d + 1 α1 = ⋯ = αm = 1 2d
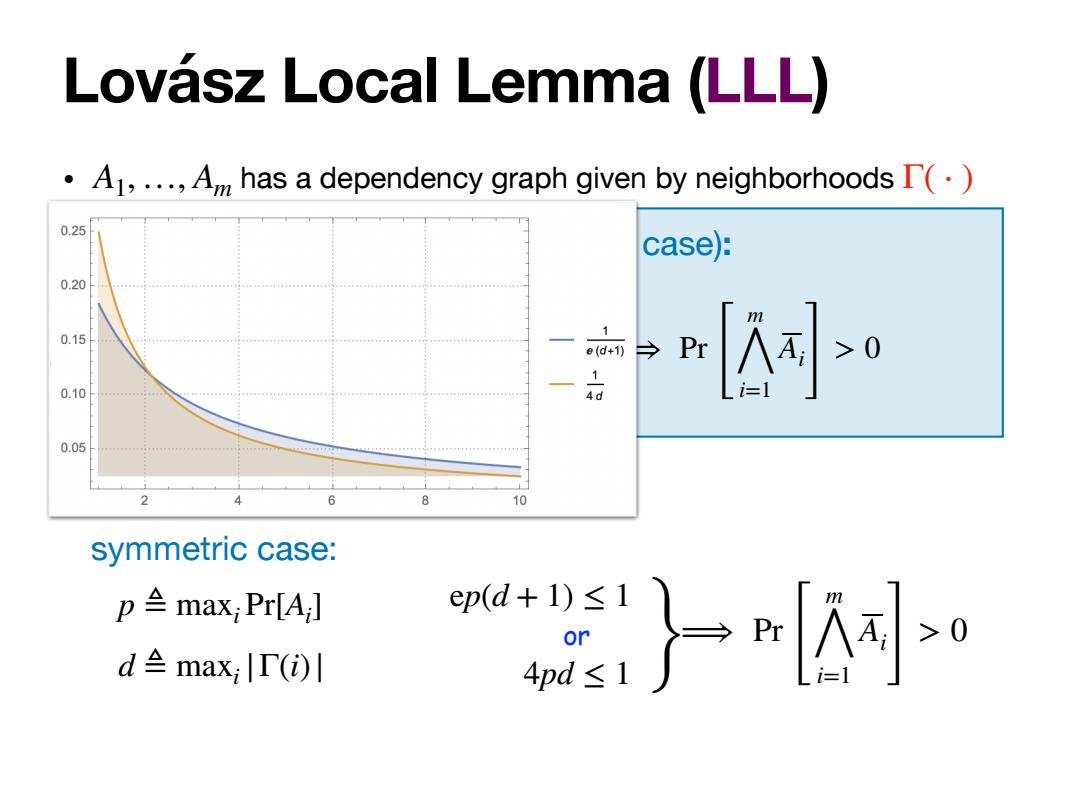
Lovasz Local Lemma (LLL) A1,...,A has a dependency graph given by neighborhoods I() 0.25 case): 0.20 0.15 e(d+1) Pr 0.10 0.05 6 8 10 symmetric case: p≌max;Pr[A] ep(d+1)≤1 or d≌max;lT(i)l 4pd≤1
Lovász Local Lemma (LLL) • A has a dependency graph given by neighborhoods 1, …, Am Γ( ⋅ ) p ≜ max i Pr[Ai ] d ≜ maxi |Γ(i)| symmetric case: ⟹ Pr [ m ⋀ i=1 Ai ] > 0 } Lovász Local Lemma (asymmetric case): ⟹ Pr [ m ⋀ i=1 Ai ] > 0 ∃α : 1,…, αm ∈ [0,1) ∀i, Pr[Ai ] ≤ αi ∏ Aj ∈Γ(Ai ) (1 − αj ) or ep(d + 1) ≤ 1 4pd ≤ 1