人教版《高中数学》全程设计训练题库（A版选修第二册，课后习题，含答案）第五章 5.3 5.3.2 第2课时 函数的最大（小）值

第2课时 函数的最大（小）值 课后训练提升 基础巩固 1.己知函数x)=x3px2-gg的图象与x轴相切于点(1,0)，则x)在区间[-1,1]上的最 大值、最小值分别为( A.0,-4 B务4 C.0 D.2,0 答案B 解折由短老得阳8中昭=子 则x)=xr3-2xr2+x,fx)=3x2-4x+1, 令x)=0,解得x=1或x=子 又)=-I=4)=0, 所以)a=务x)加im=4 2.函数x)=x44xx<1)的最值情况是() A有最大值，无最小值 B.有最大值，也有最小值 C.无最大值，有最小值 D.既无最大值，也无最小值 答案D 解析fx)=4x3-4=4(x-1)x2+x+1)】 令fx)=0,得x=1. 又x∈(1,1)且1-1,1) ∴.该方程无解，故函数x)在区间(1,1)内既无极值也无最值，故选D. 3.函数x)=2Vx+x∈(0,5的最小值为 ) A.2 B.3 c兴 D22+ 答案B 解析：由)左京==0，得x=l,且当x∈0,1)时0，当x∈(1，] 时fx)>0, .当x=1时，x)取得最小值，且最小值为1)=3 4.己知a,b为正实数，函数x)=ax3+bx+2在区间[0,1]上的最大值为4，则x)在区 间[-1,0]上的最小值为( A.0 B

第 2 课时 函数的最大(小)值 课后· 基础巩固 1.已知函数 f(x)=x3 -px2 -qx 的图象与 x 轴相切于点(1,0),则 f(x)在区间[-1,1]上的最 大值、最小值分别为( ). A.0,-4 B. 4 27 ,-4 C. 4 27 ,0 D.2,0 答案:B 解析:由题意得{ 𝑓(1) = 0, 𝑓'(1) = 0, 即 { 𝑝 + 𝑞 = 1, 3-2𝑝-𝑞 = 0, 得{ 𝑝 = 2, 𝑞 = -1. 则 f(x)=x3 -2x 2+x,f'(x)=3x 2 -4x+1, 令 f'(x)=0,解得 x=1 或 x= 1 3 , 又 f( 1 3 ) = 4 27 ,f(-1)=-4,f(1)=0, 所以 f(x)max= 4 27 ,f(x)min=-4. 2.函数 f(x)=x4 -4x(|x|<1)的最值情况是( ). A.有最大值,无最小值 B.有最大值,也有最小值 C.无最大值,有最小值 D.既无最大值,也无最小值 答案:D 解析:f'(x)=4x 3 -4=4(x-1)(x 2+x+1). 令 f'(x)=0,得 x=1. 又 x∈(-1,1)且 1∉(-1,1), ∴该方程无解,故函数 f(x)在区间(-1,1)内既无极值也无最值,故选 D. 3.函数 f(x)=2√𝑥 + 1 𝑥 ,x∈(0,5]的最小值为( ). A.2 B.3 C. 17 4 D.2√2 + 1 2 答案:B 解析:由 f'(x)= 1 √𝑥 − 1 𝑥 2 = 𝑥 3 2-1 𝑥 2 =0,得 x=1,且当 x∈(0,1)时,f'(x)<0,当 x∈(1,5] 时,f'(x)>0, ∴当 x=1 时,f(x)取得最小值,且最小值为 f(1)=3. 4.已知 a,b 为正实数,函数 f(x)=ax3+bx+2 在区间[0,1]上的最大值为 4,则 f(x)在区 间[-1,0]上的最小值为( ). A.0 B. 3 2

C.-2 D.2 答案：A 解析：因为a,b为正实数，所以x)=ar3+bx+2是增函数，所以函数x)=ax3+bx+2 在区间[0,1]上的最大值为1)=a+b+2=4,所以a+b=2. 故函数x)在区间[-1,0]上的最小值为-1)=-(a+b)+2=0. 5.若函数x)=asin x+2sin3x在x=处取得最值，则a等于()】 A.2 B.1 C. 3 D.0 答案A 解析：“)在x=处取得最值， ∴x=是函数x)的极值点 又fx)=acos x+cos3x, 份acos+cosπ=0，解得a=2 6.(多选题)函数y=x)的导函数y=fx)的图象如图所示，则下列结论错误的是 () y=f'(x) A.-3是函数y=x)的极值点 B.-1是函数y=x)的最小值点 Cy=x)在区间(-3,1)内单调递增 Dy=x)的图象在点(OO)处的切线斜率小于0 答案BD 解析：由导函数图象可知f八-3)=0， 当x∈(-oo,-3)时fx)<0,当x∈(-3,1)时，fx)≥0，当且仅当x=-1时fx)=0, .函数y=儿x)在区间(-0，-3)上单调递减，在区间(-3,1)内单调递增， 从而-3是函数y=术x)的极小值点，故C正确，A正确； x)在区间（←3,1）内单调递增 -1不是函数y=x)的最小值点，故B错误， :函数y=x)在x=0处的导数大于0， .切线的斜率大于0，故D错误 综上，选BD 7.若关于x的不等式x33x+3+a≤0恒成立，其中-2≤x≤3，则实数a的最大值为 () A.1 B.-1 C.-5 D.-21

C.-2 D.2 答案:A 解析:因为 a,b 为正实数,所以 f(x)=ax3+bx+2 是增函数,所以函数 f(x)=ax3+bx+2 在区间[0,1]上的最大值为 f(1)=a+b+2=4,所以 a+b=2. 故函数 f(x)在区间[-1,0]上的最小值为 f(-1)=-(a+b)+2=0. 5.若函数 f(x)=asin x+1 3 sin 3x 在 x= π 3处取得最值,则 a 等于( ). A.2 B.1 C. 2√3 3 D.0 答案:A 解析:∵f(x)在 x= π 3处取得最值, ∴x= π 3是函数 f(x)的极值点. 又 f'(x)=acos x+cos 3x, ∴f'( π 3 )=acos π 3 +cos π=0,解得 a=2. 6.(多选题)函数 y=f(x)的导函数 y=f'(x)的图象如图所示,则下列结论错误的是 ( ). A.-3 是函数 y=f(x)的极值点 B.-1 是函数 y=f(x)的最小值点 C.y=f(x)在区间(-3,1)内单调递增 D.y=f(x)的图象在点(0,f(0))处的切线斜率小于 0 答案:BD 解析:由导函数图象可知,f'(-3)=0, 当 x∈(-∞,-3)时,f'(x)<0,当 x∈(-3,1)时,f'(x)≥0,当且仅当 x=-1 时,f'(x)=0, ∴函数 y=f(x)在区间(-∞,-3)上单调递减,在区间(-3,1)内单调递增, 从而-3 是函数 y=f(x)的极小值点,故 C 正确,A 正确; ∵f(x)在区间(-3,1)内单调递增, ∴-1 不是函数 y=f(x)的最小值点,故 B 错误; ∵函数 y=f(x)在 x=0 处的导数大于 0, ∴切线的斜率大于 0,故 D 错误. 综上,选 BD. 7.若关于 x 的不等式 x 3 -3x+3+a≤0 恒成立,其中-2≤x≤3,则实数 a 的最大值为 ( ). A.1 B.-1 C.-5 D.-21

答案D 解析：若关于x的不等式x3-3x+3+a≤0在区间[2,3]上恒成立，则a≤x3+3x-3在 区间[-2,3]上恒成立，令x)=-x3+3x-3,x∈[-2,3]，则fx)=-3x2+3=-3(x+1)x-1),令 fx)>0,解得-1<x<1,令fx)<0,解得x>1或x<-1,故x)在区间[-2，-1)内单调递减 在区间(-1,1)内单调递增，在区间(1,3]上单调递减，而-2)=-1，-1)=-5,1)= 1,3)=-21,故a≤-21，故a的最大值为-21 8函数)华∈P2,2)的最大值是 最小值是 答案22 解析x)=+14xx2x =41x2) (x2+1)2 (x2+1)2 =41+-四，令fx)=0,得x1=-l,n=1 (x2+1)2 由-2)=号-1)=-21)=22)=8 ∴.x)max=2,x)min=-2 9.已知函数x)=导r3+2axr2+3x(a>0)的导数fw)的最大值为5，则函数x)的图象在 点(11)处的切线方程是 答案：15x-3y-2=0 解析：.fx)=-2x2+4ax+3=-2x-a2+3+2a2, fx)max=3+2a2=5,.a>0,∴.a=1. ∴fx)=-2x2+4x+3,f1)=-2+4+3=5 又1)号+2+3-号 所求切线方程为y3=5x-1) 即15x-3y-2=0 10.已知函数x)=32-x+m在区间[0,1]上的最小值为号则实数m的值 为 答案2 解析：由)子r32-x+m,可得fx)=2-2x-l,令2-2x1=0,可得x=1±VZ 当x∈(1-√2,1+V②时fx)<0,即函数x)在区间(1-√2,1+V②)内单调递减，即x)在 区间0,1]上单调递减，故x)在区间0,1]上的最小值为1)，所以51-1+m=三解得 m=2. 11.已知函数x)=a4lnx+bx4-c(x>0)在x=1处取得极值-3-c,其中a,b,c为常数 (1)试确定a,b的值； (2)求函数x)的单调区间： (3)若对任意x>0,不等式x)≥-2c2恒成立，求实数c的取值范围 解(1)由x)在x=1处取得极值-3-c知1)=b-c=-3-c,得b=-3. 又fx)=4ar3lnx+ar4.二+4bx3=x3(4alnx+a+4b),由f1)=0,得a+4b=0,则a=-4b=12. (2)由(1)知fx)=48x3lnx(x>0)

答案:D 解析:若关于 x 的不等式 x 3 -3x+3+a≤0 在区间[-2,3]上恒成立,则 a≤-x 3+3x-3 在 区间[-2,3]上恒成立,令 f(x)=-x 3+3x-3,x∈[-2,3],则 f'(x)=-3x 2+3=-3(x+1)(x-1),令 f'(x)>0,解得-1<x<1,令 f'(x)<0,解得 x>1 或 x<-1,故 f(x)在区间[-2,-1)内单调递减, 在区间(-1,1)内单调递增,在区间(1,3]上单调递减,而 f(-2)=-1,f(-1)=-5,f(1)=- 1,f(3)=-21,故 a≤-21,故 a 的最大值为-21. 8.函数 f(x)= 4𝑥 𝑥 2 +1 (x∈[-2,2])的最大值是 ,最小值是 . 答案:2 -2 解析:f'(x)= 4(𝑥 2 +1)-4𝑥×2𝑥 (𝑥 2 +1) 2 = 4(1-𝑥 2 ) (𝑥 2 +1) 2 = 4(1+𝑥)(1-𝑥) (𝑥 2 +1) 2 ,令 f'(x)=0,得 x1=-1,x2=1. 由 f(-2)=- 8 5 ,f(-1)=-2,f(1)=2,f(2)= 8 5 , ∴f(x)max=2,f(x)min=-2. 9.已知函数 f(x)=- 2 3 x 3+2ax2+3x(a>0)的导数 f'(x)的最大值为 5,则函数 f(x)的图象在 点(1,f(1))处的切线方程是 . 答案:15x-3y-2=0 解析:∵f'(x)=-2x 2+4ax+3=-2(x-a) 2+3+2a 2 , ∴f'(x)max=3+2a 2=5,∵a>0,∴a=1. ∴f'(x)=-2x 2+4x+3,f'(1)=-2+4+3=5. 又 f(1)=- 2 3 +2+3= 13 3 , ∴所求切线方程为 y- 13 3 =5(x-1). 即 15x-3y-2=0. 10.已知函数 f(x)= 1 3 x 3 -x 2 -x+m 在区间[0,1]上的最小值为1 3 ,则实数 m 的值 为 . 答案:2 解析:由 f(x)= 1 3 x 3 -x 2 -x+m,可得 f'(x)=x2 -2x-1,令 x 2 -2x-1=0,可得 x=1±√2. 当 x∈(1-√2,1+√2)时,f'(x)<0,即函数 f(x)在区间(1-√2,1+√2)内单调递减,即 f(x)在 区间[0,1]上单调递减,故 f(x)在区间[0,1]上的最小值为 f(1),所以1 3 -1-1+m=1 3 ,解得 m=2. 11.已知函数 f(x)=ax4 ln x+bx4 -c(x>0)在 x=1 处取得极值-3-c,其中 a,b,c 为常数. (1)试确定 a,b 的值; (2)求函数 f(x)的单调区间; (3)若对任意 x>0,不等式 f(x)≥-2c 2 恒成立,求实数 c 的取值范围. 解:(1)由 f(x)在 x=1 处取得极值-3-c 知 f(1)=b-c=-3-c,得 b=-3. 又 f'(x)=4ax3 ln x+ax4· 1 𝑥 +4bx3=x3 (4aln x+a+4b),由 f'(1)=0,得 a+4b=0,则 a=-4b=12. (2)由(1)知 f'(x)=48x 3 ln x(x>0)

令fx)=0,得x=1. 当0<x<1时fx)<0,x)单调递减； 当x>1时fx)>0,x)单调递增 因此x)的单调递减区间为(0,1)，单调递增区间为(1，+o). (3)由(2)知1)=-3-c既是极小值，也是区间(0，+o)内的最小值，要使x)≥-2c2恒成 立，只需-3-c≥-2c2,即2c2-c-3≥0.解得c≥三或c≤-1 故实数c的取值范围为(0，-U昼+∞） 拓展提高 1.己知函数x)=-x2-2x+3在区间[a,2]上的最大值为5，则a等于() A月 D或 答案：C 解析：由题意知a<2,令fx)=-2x-2=0,解得x=-1. 当a≤-1时，x)的最大值为-1)=4，不符合题意. 当-1<a<2时x)在区间[a,2]上单调递减，a)最大， 则有2-2a+3-解得a=或a=舍去)所以a=之 2.若函数x)=-x3-3x2+1在区间[a+o)内的最大值为1，则a的取值范围是( A.[-3,+0) B.(-3,+o0) C.(-3,0) D.[-3,0] 答案D 解析：x)=-x3-3x2+1, fx)=-3x2-6x,令fx)=0,解得x=0或x=-2,当x变化时fx)x)的变化情况如下 表 (-00,-2) -2 -2,0) 0,+0∞) f(x) 0 Kx) 单调递减 极小值 单调递增 极大值 单调递减 由x)=-x3-3x2+1在区间[a,+o)内的最大值为1，得-x3-3x2+1=1,解得x=0或x=-3. 当x>0时x)f0)=1,当x<-3时x)>-3)=1,∴.a的取值范围为[-3,0] 3.已知函数x)=-x3+ar2-4在x=2处取得极值，若m,n∈[-1,1]，则m)+fn)的最小 值是( A.15 B.-15 C.10 D.-13 答案D

令 f'(x)=0,得 x=1. 当 0<x<1 时,f'(x)<0,f(x)单调递减; 当 x>1 时,f'(x)>0,f(x)单调递增. 因此,f(x)的单调递减区间为(0,1),单调递增区间为(1,+∞). (3)由(2)知 f(1)=-3-c 既是极小值,也是区间(0,+∞)内的最小值,要使 f(x)≥-2c 2 恒成 立,只需-3-c≥-2c 2 ,即 2c 2 -c-3≥0.解得 c≥ 3 2 或 c≤-1. 故实数 c 的取值范围为(-∞,-1]∪[ 3 2 , +∞). 拓展提高 1.已知函数 f(x)=-x 2 -2x+3 在区间[a,2]上的最大值为15 4 ,则 a 等于( ). A.- 3 2 B. 1 2 C.- 1 2 D. 1 2或- 3 2 答案:C 解析:由题意知 a<2,令 f'(x)=-2x-2=0,解得 x=-1. 当 a≤-1 时,f(x)的最大值为 f(-1)=4,不符合题意. 当-1<a<2 时,f(x)在区间[a,2]上单调递减,f(a)最大, 则有-a 2 -2a+3= 15 4 ,解得 a=- 1 2或 a=- 3 2 (舍去).所以 a=- 1 2 . 2.若函数 f(x)=-x 3 -3x 2+1 在区间[a,+∞)内的最大值为 1,则 a 的取值范围是( ). A.[-3,+∞) B.(-3,+∞) C.(-3,0) D.[-3,0] 答案:D 解析:∵f(x)=-x 3 -3x 2+1, ∴f'(x)=-3x 2 -6x,令 f'(x)=0,解得 x=0 或 x=-2,当 x 变化时,f'(x),f(x)的变化情况如下 表: x (-∞,-2) -2 (-2,0) 0 (0,+∞) f'(x) - 0 + 0 - f(x) 单调递减 极小值 单调递增 极大值 单调递减 由 f(x)=-x 3 -3x 2+1 在区间[a,+∞)内的最大值为 1,得-x 3 -3x 2+1=1,解得 x=0 或 x=-3. 当 x>0 时,f(x)<f(0)=1,当 x<-3 时,f(x)>f(-3)=1,∴a 的取值范围为[-3,0]. 3.已知函数 f(x)=-x 3+ax2 -4 在 x=2 处取得极值,若 m,n∈[-1,1],则 f(m)+f'(n)的最小 值是( ). A.15 B.-15 C.10 D.-13 答案:D

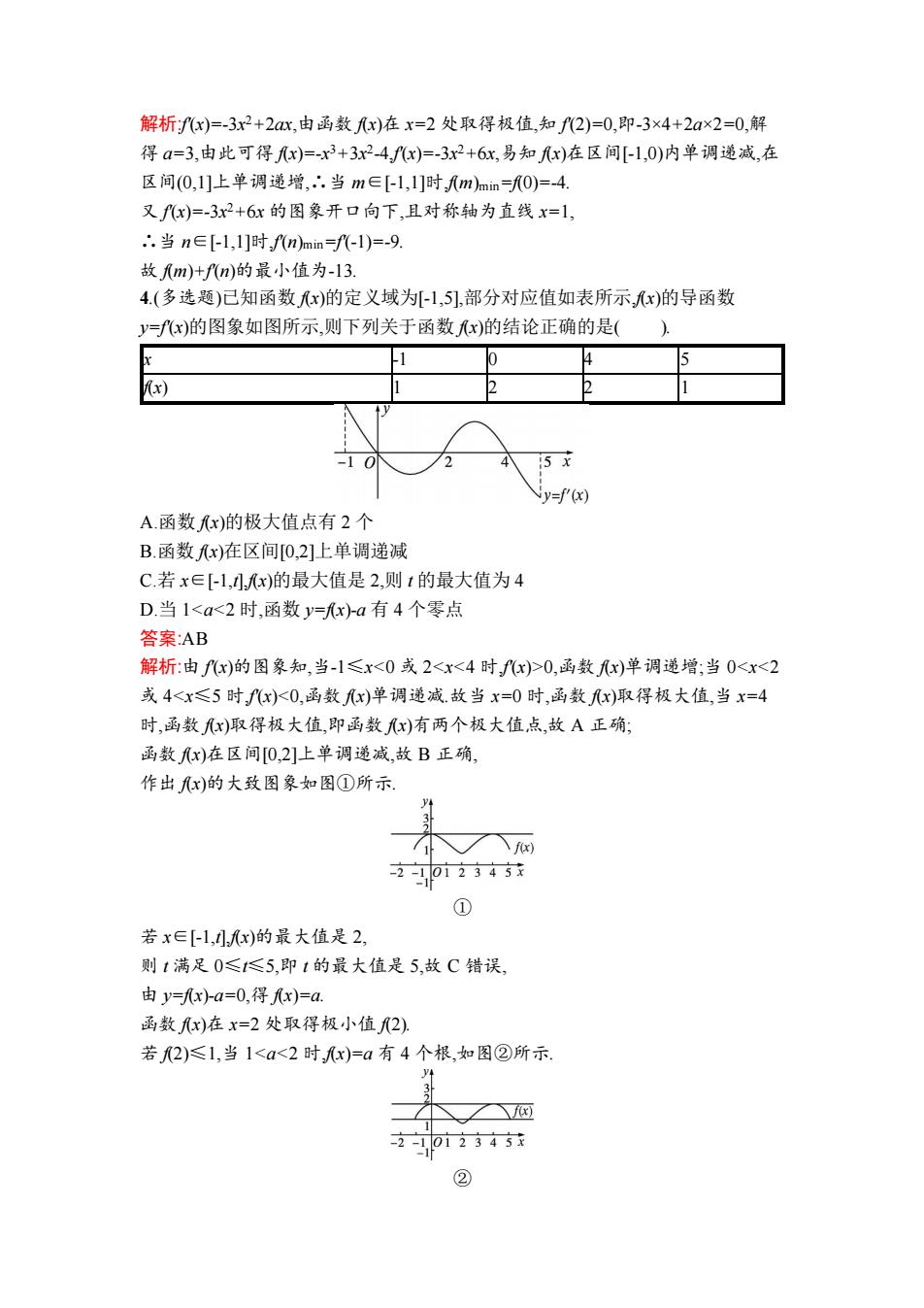
解析fx)=-3x2+2ax,由函数x)在x=2处取得极值，知f2)=0,即-3×4+2a×2=0,解 得a=3,由此可得x)=-x3+3x2-4,x)=-3x2+6x,易知x)在区间[-1,0)内单调递减，在 区间(0,1]上单调递增，.当m∈[-l,1]时，m)mm=f0)=-4. 又fx)=-3x2+6x的图象开口向下，且对称轴为直线x=1, .当n∈[-1，l]时fnm)mim=f-l)=-9. 故m)+fn)的最小值为-l3 4.(多选题)已知函数x)的定义域为[-1,5]，部分对应值如表所示，x)的导函数 y=x)的图象如图所示，则下列关于函数x)的结论正确的是( 4 ) i5 x =f(x) A.函数x)的极大值点有2个 B.函数x)在区间[0,2]上单调递减 C.若x∈[-1，x)的最大值是2，则1的最大值为4 D.当1<a<2时，函数y=x)a有4个零点 答案：AB 解析：由fx)的图象知，当-1≤x<0或2<x<4时fx)>0,函数x)单调递增；当0<xr<2 或4<x≤5时fx<0,函数x)单调递减.故当x=0时，函数x)取得极大值，当x=4 时，函数x)取得极大值，即函数x)有两个极大值点，故A正确； 函数x)在区间[0,2]上单调递减，故B正确， 作出x)的大致图象如图①所示 f) 21012345x ① 若x∈[-1，，x)的最大值是2， 则1满足0≤≤5，即1的最大值是5，故C错误， 由y=fx)-a=0,得x)=a. 函数x)在x=2处取得极小值2) 若2)≤1，当1<a<2时，x)=a有4个根，如图②所示 201234 ②

解析:f'(x)=-3x 2+2ax,由函数 f(x)在 x=2 处取得极值,知 f'(2)=0,即-3×4+2a×2=0,解 得 a=3,由此可得 f(x)=-x 3+3x 2 -4,f'(x)=-3x 2+6x,易知 f(x)在区间[-1,0)内单调递减,在 区间(0,1]上单调递增,∴当 m∈[-1,1]时,f(m)min=f(0)=-4. 又 f'(x)=-3x 2+6x 的图象开口向下,且对称轴为直线 x=1, ∴当 n∈[-1,1]时,f'(n)min=f'(-1)=-9. 故 f(m)+f'(n)的最小值为-13. 4.(多选题)已知函数 f(x)的定义域为[-1,5],部分对应值如表所示,f(x)的导函数 y=f'(x)的图象如图所示,则下列关于函数 f(x)的结论正确的是( ). x -1 0 4 5 f(x) 1 2 2 1 A.函数 f(x)的极大值点有 2 个 B.函数 f(x)在区间[0,2]上单调递减 C.若 x∈[-1,t],f(x)的最大值是 2,则 t 的最大值为 4 D.当 1<a<2 时,函数 y=f(x)-a 有 4 个零点 答案:AB 解析:由 f'(x)的图象知,当-1≤x<0 或 2<x<4 时,f'(x)>0,函数 f(x)单调递增;当 0<x<2 或 4<x≤5 时,f'(x)<0,函数 f(x)单调递减.故当 x=0 时,函数 f(x)取得极大值,当 x=4 时,函数 f(x)取得极大值,即函数 f(x)有两个极大值点,故 A 正确; 函数 f(x)在区间[0,2]上单调递减,故 B 正确, 作出 f(x)的大致图象如图①所示. ① 若 x∈[-1,t],f(x)的最大值是 2, 则 t 满足 0≤t≤5,即 t 的最大值是 5,故 C 错误, 由 y=f(x)-a=0,得 f(x)=a. 函数 f(x)在 x=2 处取得极小值 f(2). 若 f(2)≤1,当 1<a<2 时,f(x)=a 有 4 个根,如图②所示. ②