应力状态和强度理论O考虑剪应力互等和三角变换,得:a +a,Ox-0Ocos 2α - t, sin 2αQα22y同理:图1OXC.-oysin 2α + t cos2αTαOd2aO.Rd代ya0x图2
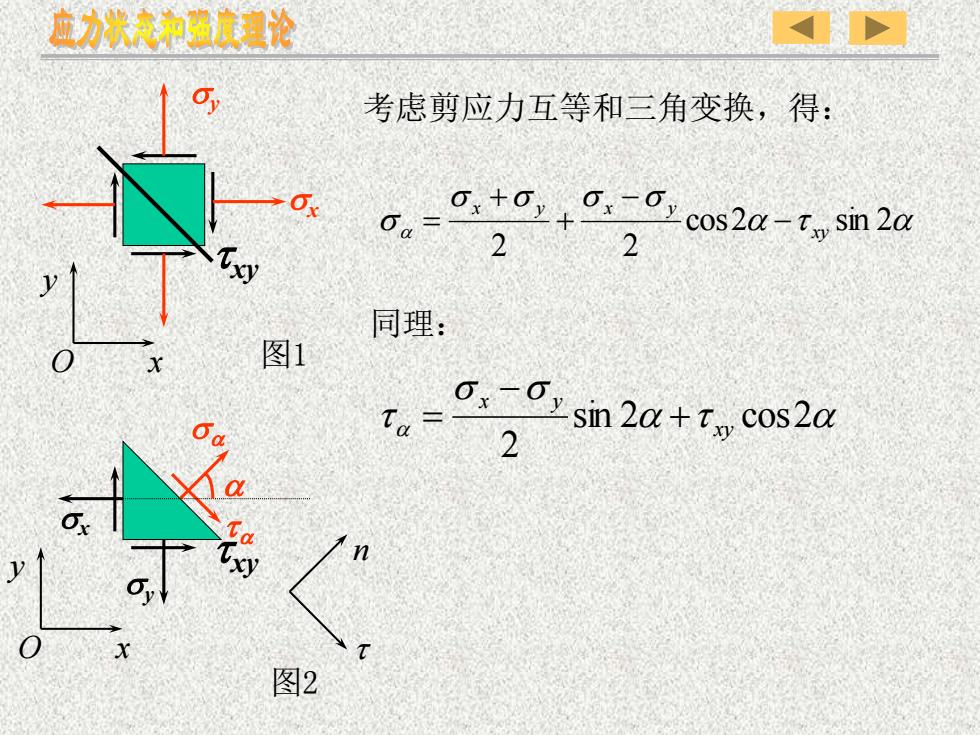
x 图1 y sx txy sy O sy txy sx s t x y O t n 图2 t s s s s s cos2 sin 2 2 2 xy x y x y − − + + = t s s t sin 2 cos2 2 xy x y + − = 考虑剪应力互等和三角变换,得: 同理:

应力状态和强度理论二、极值应力Ado.--(o,0,bin200-2tycos20=0dα lα-αo由此的两个驻点:2txy元tg2α和两各极值:(αoi+αo10y2ayma-oaTxyt。。=0:极值正应力就是主应力!OX
: ( )sin2 0 2 cos2 0 0 0 =− − − = = s s t s x y xy d d 令 二、极值应力 x y xy s s t − = − 2 、( )和两各极值: tg2 0 由此的两个驻点: 2 01 01 + t 0 =0极值正应力就是主应力! ) 2 2 2 2 xy x y x y min max t s s s s s s + − ± + = ( ´ ´ x y sx txy sy O
应力状态和强度理论0*-0mx; 0;=0 mn生α"在剪应力相对的项限内,6单元体S且偏向于g,及g,大的一侧aTxyyAdta0.-0OX-0tg2αf2txdα lα=αiEeL元,即极值剪应力面与主面成45°α0=α +4
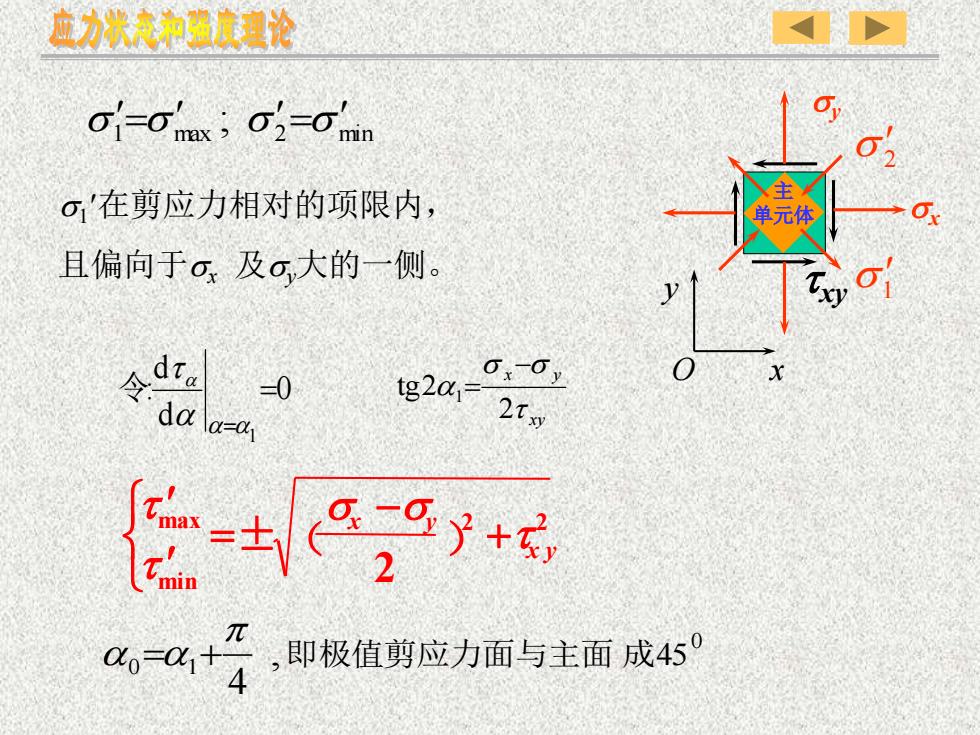
x y sx txy sy O 主 s1 在剪应力相对的项限内, 单元体 且偏向于sx 及sy大的一侧。 0 d d : 1 = = t 令 xy x y t s s 2 tg2 1 − = 2 2 2 x y x y min max t s s t t + − =± ( ) 0 0 1 , 45 4 即极值剪应力面与主面 成 = + 1 max 2 min s =s ; s =s s 2 s1

应力状态和强度理论例1图示圆轴中,已知:圆轴直径d-100mm,轴向拉力F=500kN,外力矩M=7kN·m。求C点α =-30°截面上的应力。PCLXa口Catxt.1火(a)(b)解:C点应力状态如图b所示,其拉应力和切应力为:F500 ×103= 63.7MPa0A元×10024
解:C点应力状态如图b所示,其拉应力和切应力为: 63.7MPa 100 4 π 500 10 2 3 = = = A F s x 例1 图示圆轴中,已知:圆轴直径d=100mm,轴向拉 力F=500kN,外力矩Me =7kN·m。求C点 =−30°截面 上的应力。 (b) C x tx sx sx t x t y t y y (a) x T F T C F

应力状态和强度理论7×10°M.-35.7MPaTWp元×1003yI16O图示斜截面上应力分量为:30 +0g.-0~ cos(- 60 )- , sin (- 60°)0+-30°22= 16.9MPa9.-0sin 2α + t. cos2α = -45.4MPaT-30°2
( ) ( ) 16.9MPa cos 60 sin 60 2 0 2 0 3 0 = − − − − + + = − x x x t s s s sin 2 cos 2 45.4MPa 2 0 3 0 + = − − = − t s t x x 图示斜截面上应力分量为: 35.7MPa 100 16 π 7 10 3 6 P e = − = = − W M x t C x t x sx sx t x t y ty y 30° n s t -30 -30° °