应力状态和强度理论例2分析受扭构件的破坏规律解:0确定危险点并画其原Tyx始单元体9,=9,-0MMTxy三T-WpTxy②求极值应力Tyxo' a,+o,+.oy?+t?Vg, 22-+/t,-±t0
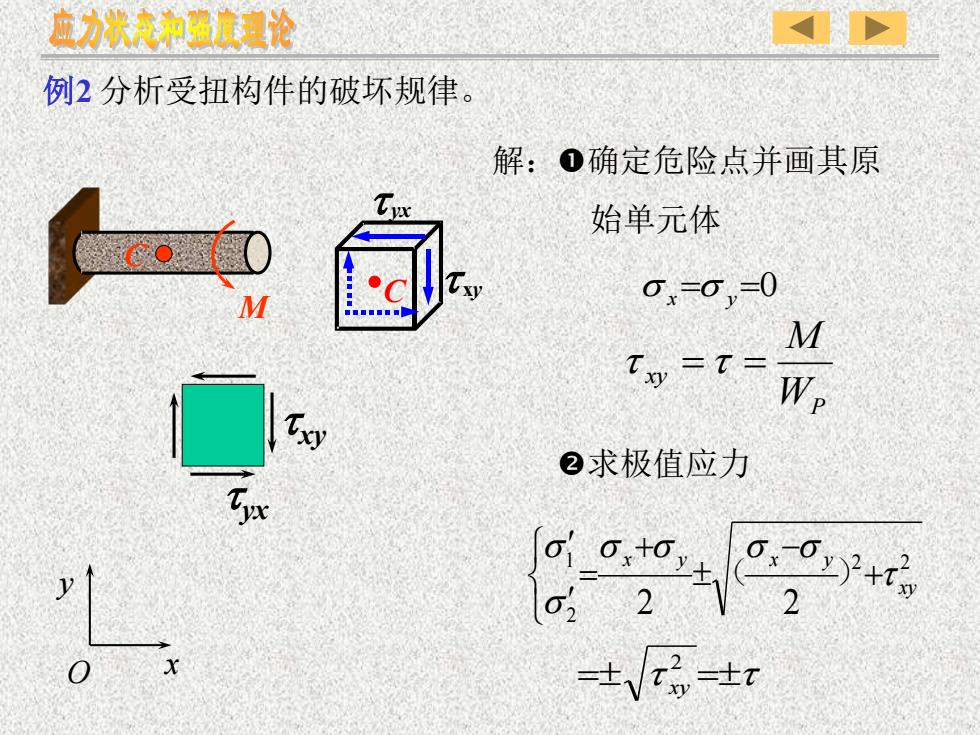
例2 分析受扭构件的破坏规律。 解:确定危险点并画其原 始单元体 求极值应力 s x =s y =0 P xy W M t =t = 2 2 2 1 2 2 xy x y x y t s s s s s s + − + = ( ) = t =t 2 xy C t xy t yx M C x y O txy t yx
应力状态和强度理论2t.0 -t,02-0,0,=-T=00. .0%,=45°tg2αa-9.)+t,-+tmx=+,0,-0,-0:α-0tg2α,2txy③破坏分析低碳钢低碳钢:o-240MPa;t.-200MPa灰口铸铁:αLb-98~280MPa铸铁α yb=640~960MPa;t,=198~300MPa
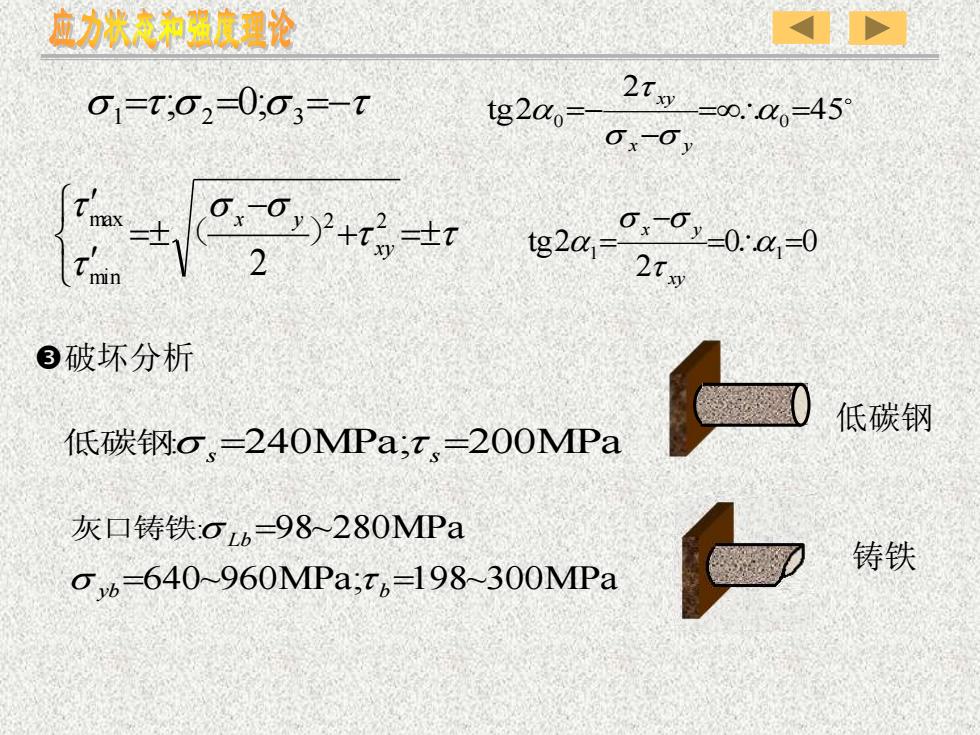
破坏分析 t t s s tt + = − = 2 2 min max 2 xy x y ( ) s =t s = s = −t 1 2 3 ; 0 ; 45 2 tg 2 0 = 0 = − = − s s t x y xy 0 0 2 tg 2 1 = 1 = − = t s s xy x y 低碳钢:s s =240MPa;t s =200MPa 640~960MPa; 198~300MPa : 98~280MPa = = = yb b Lb s t 灰口铸铁 s 低碳钢 铸铁

应力状态和强度理论810.3二向应力状态分析的图解法、应力圆a +ox-0cos2α-t n,sin 202O22Txsin 2α+t.,cos2αO对上述方程消去参数(2α),得:4-0O2T6a.CoCg,此方程曲线为圆应力圆(或莫尔圆-O由德国工程师:OttoMohr引入)
§10.3 二向应力状态分析的图解法 + − = − − + + = t s s t t s s s s s sin2 cos2 2 cos2 sin2 2 2 xy x y xy x y x y 2 2 2 2 2 2 xy x y x y t s s t s s s + − + = + − 对上述方程消去参数(2),得: 一、应力圆 x y sx txy sy O sy txy sx s t x y O t n 此方程曲线为圆—应力圆(或莫尔圆, 由德国工程师:Otto Mohr引入)

应力状态分析和强度理论On二、应力圆的画法O0建立应力坐标系,如下图所示6(注意选好比例尺).dTxy②在坐标系内画出点A(α,)和0B(oy, Tx)子DC(Oα, Tα)nRdx③AB与α轴的交点C便是圆心。A(ox,txy)2αQα0④以C为圆心,以AC为半径画B(o,, tx)圆一应力圆;
建立应力坐标系,如下图所示, (注意选好比例尺) 二、应力圆的画法 在坐标系内画出点A(s x,txy)和 B(sy,tyx) AB与s轴的交点C便是圆心。 以C为圆心,以AC为半径画 圆——应力圆; sx txy sy x y O n s t O s t C A(sx ,t xy) B(sy ,t yx) x 2 n D( s , t )
应力状态和强度理论On三、单元体与应力圆的对应关系Oα面上的应力(α,)o应力圆上一点(α,tα)Ry③α面的法线应力圆的半径0D(Oα, Ta)nTax③两面夹角α两半径夹角2α;A(ox,txy)2α且转向一致。dα0B(oy, tx)
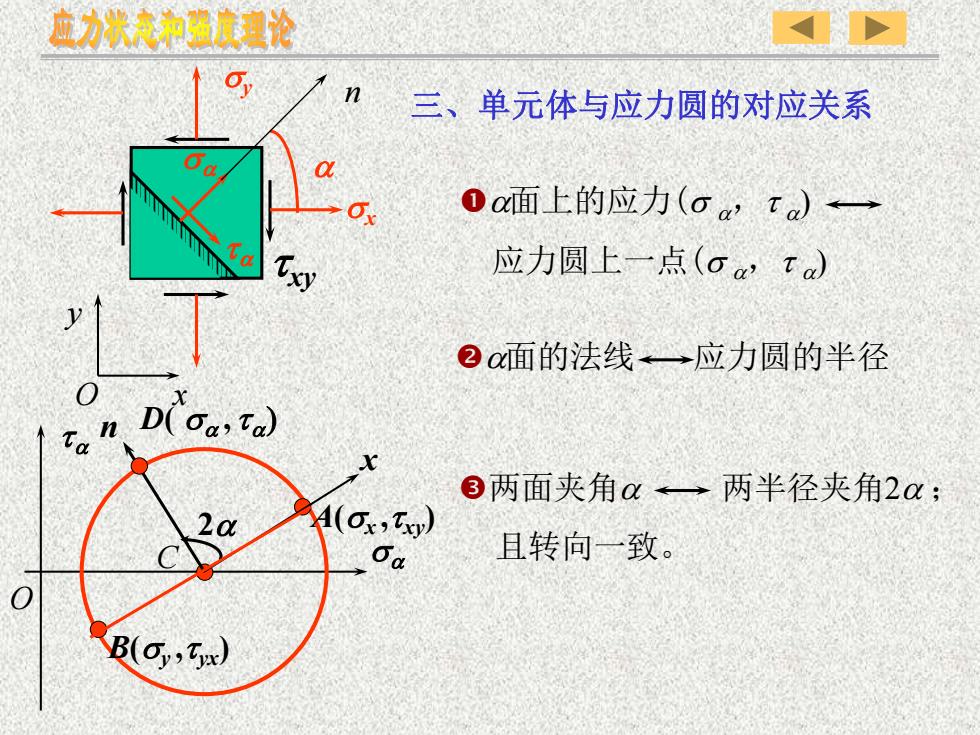
sx txy sy x y O n s t O s t C A(sx ,t xy) B(sy ,t yx) x 2 n D( s , t ) 三、单元体与应力圆的对应关系 面上的应力(s ,t ) 应力圆上一点(s ,t ) 面的法线 应力圆的半径 两面夹角 两半径夹角2 ; 且转向一致