石河子大学：《建筑结构抗震》课程教学资源（课件讲稿）第3章 结构地震反应分析与抗震计算

建筑结构抗震 第3章结构地震反应分析与抗震验算 1.方程的齐次解；ⅰ自由振动： 当5=0（无阻尼） x(1)=xocos@t+ %osin@t x(f 无阻尼单自由度体系自由振动为简谐振动 土木专业 水建学院

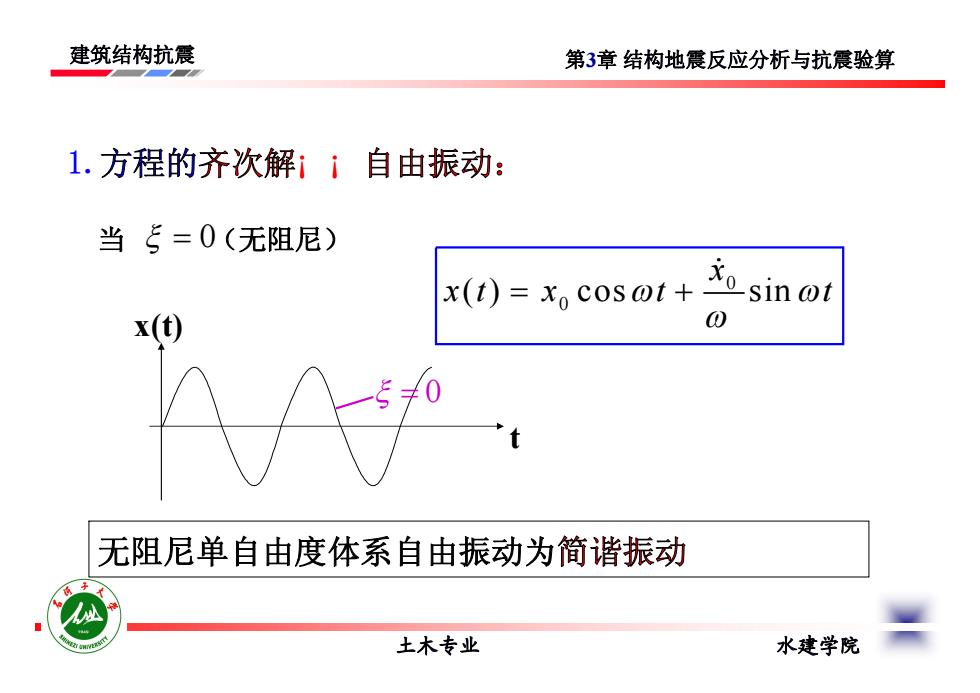
建筑结构抗震 土木专业 水建学院 第3章 结构地震反应分析与抗震验算 当   0（无阻尼） 0 0 ( ) cos sin x x t x t t     无阻尼单自由度体系自由振动为简谐振动 t x(t)   0 1.方程的齐次解¡ ¡ 自由振动：

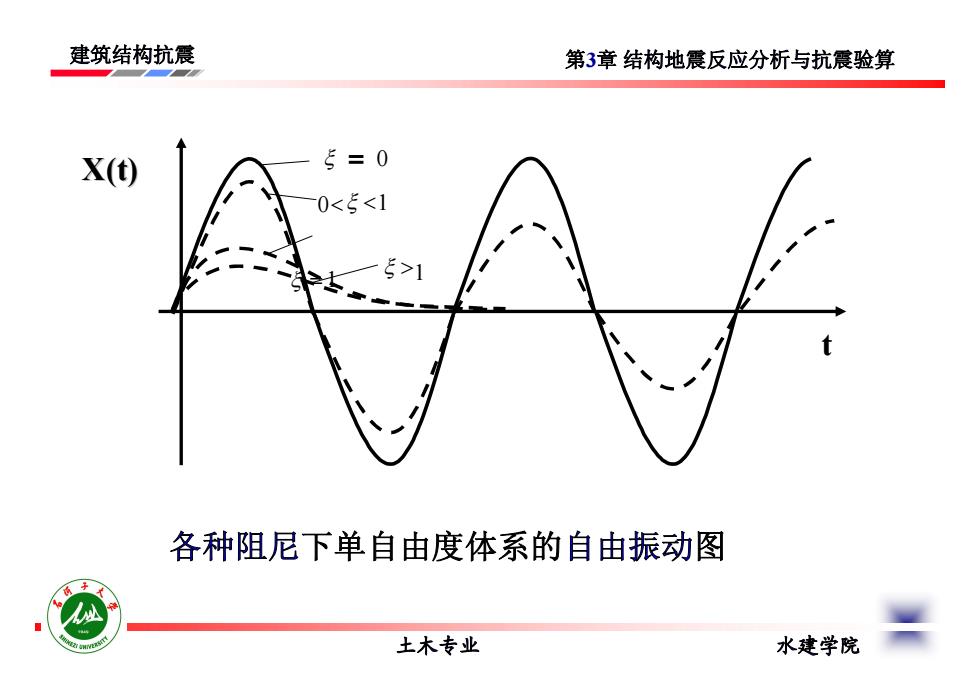
建筑结构抗震 第3章结构地震反应分析与抗震验算 X() 5=0 0<5<1 7 5 各种阻尼下单自由度体系的自由振动图 土木专业 水建学院

建筑结构抗震 土木专业 水建学院 第3章 结构地震反应分析与抗震验算 各种阻尼下单自由度体系的自由振动图 t  = 0 0 1  1  1 X(t)

建筑结构抗震 第3章结构地震反应分析与抗震验算 1.方程的齐次解；ⅰ自由振动： i if 固有频率 m π T=2 =2π 1 ii固有周期 由上式可见，结构的自振周期与其质量和刚度的大 小有关。质量越大，则其周期就越长，而刚度越大，则 其周期就越短。 自振周期是结构的一种固有属性，也是结构本身一 个很重要的动力特性。 土木专业 水建学院

建筑结构抗震 土木专业 水建学院 第3章 结构地震反应分析与抗震验算 k m   ¡ ¡ 固有频率 k m T    2 2   ¡ ¡ 固有周期 ? 由上式可见，结构的自振周期与其质量和刚度的大 小有关。质量越大，则其周期就越长，而刚度越大，则 其周期就越短。 ? 自振周期是结构的一种固有属性，也是结构本身一 个很重要的动力特性。 1.方程的齐次解¡ ¡ 自由振动：

建筑结构抗震 第3章结构地震反应分析与抗震验算 ⅰ3.1单自由度体系的弹性地震反应分析 三、运动方程的解 2.方程的特解Iⅰⅰ简谐强迫振动： 地面简谐运动 ◆使体系产生简谐强迫振动 设xg)=Asin0g1,代入运动方程求+25ωx+02x=-求g Aⅰ地面运动振幅 →求+205x+02x=-A0g2sin0et 方程的特解（零初始条件x(0)=0(0))0 土木专业 水建学院

建筑结构抗震 土木专业 水建学院 第3章 结构地震反应分析与抗震验算 ¡ 3.1 单自由度体系的弹性地震反应分析 2.方程的特解Ⅰ¡ ¡ 简谐强迫振动： 地面简谐运动 使体系产生简谐强迫振动 2 2 2 sin g g x  x   x  A  t 方程的特解（零初始条件 x(0)  0 x(0) ）0 x x x x g        2 设 xg (t)  Asing t ，代入运动方程 2  A ¡ 地面运动振幅 三、运动方程的解

建筑结构抗震 第3章结构地震反应分析与抗震验算 2.方程的特解Iⅰⅰ简谐强迫振动： 1-( x(t)= 初位移x(0)=0 初速度 (0)=0 化简为 x(t)=Bsin(@gt+p) Bⅰ体系质点的振幅 土木专业 水建学院

建筑结构抗震 土木专业 水建学院 第3章 结构地震反应分析与抗震验算 2.方程的特解Ⅰ¡ ¡ 简谐强迫振动： 2 2 2 2 2 1 ( ) 2 ( ) ( ) 1 ( ) sin 2 cos ( )                                              g g g g g g g A t t x t x(t)  B sin( t   ) 化简为 g B ¡ 体系质点的振幅 初位移 x(0)  0 初速度 x(0)  0