石河子大学：《建筑结构抗震》课程教学资源（课件讲稿）第3章 结构地震反应分析与抗震计算

建筑结构抗震 第3章结构地震反应分析与抗震验算 2.方程的特解Iⅱⅰ简谐强迫振动： B (0g10)2 振幅放大系数 0g/0=1 ◆ 达到最大值 ◆ 共振 0.20.5 0g10 图单自由度体系简谐地面强迫振动振幅放大系数 土木专业 水建学院

建筑结构抗震 土木专业 水建学院 第3章 结构地震反应分析与抗震验算 2.方程的特解Ⅰ¡ ¡ 简谐强迫振动： 振幅放大系数 2 2 2 2 1 ( ) 2 ( ) ( / )                         g g g A B g / 1 共振 0.2 0.5 1 2 5 / g  1 2 图 单自由度体系简谐地面强迫振动振幅放大系数  达到最大值

建筑结构抗震 第3章结构地震反应分析与抗震验算 3.方程的特解II11冲击强迫振动（瞬时） 地面冲击运动： 0≤x≤dt g() 0 r >dt 对质点冲击力： e-- g 0≤r≤dt t dt 质点加速度(0~dt)： a= 图地面冲击运动 m dt时刻的速度： V=p dt=-gdt 1P dt时刻的位移： d= (dt)2≈0 2 m 土木专业 水建学院

建筑结构抗震 土木专业 水建学院 第3章 结构地震反应分析与抗震验算 3.方程的特解II¡ ¡ 冲击强迫振动（瞬时） 图 地面冲击运动 地面冲击运动：        dt x dt x g g    0 0 ( )   对质点冲击力：         dt mx dt P g   0  0 质点加速度（0～dt）： g x m P a    dt时刻的速度： dt x dt m P V g    dt时刻的位移： ( ) 0 2 1 2  dt  m P d

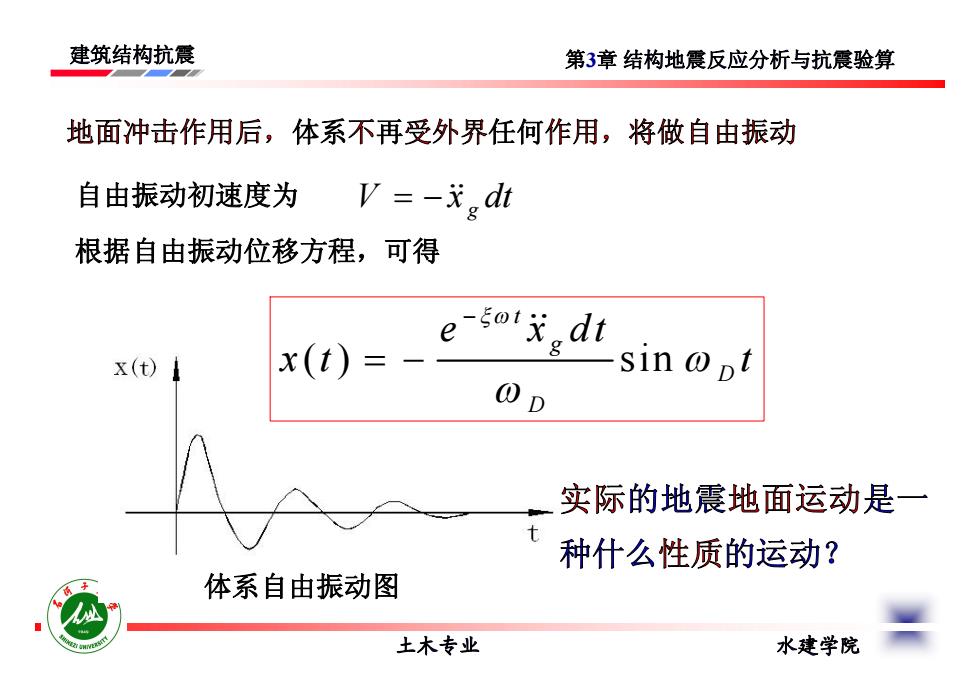
建筑结构抗震 第3章结构地震反应分析与抗震验算 地面冲击作用后，体系不再受外界任何作用，将做自由振动 自由振动初速度为 V=-%dt 根据自由振动位移方程，可得 x(t) x(t) sin @pt @p 实际的地震地面运动是一 种什么性质的运动？ 体系自由振动图 土木专业 水建学院

建筑结构抗震 土木专业 水建学院 第3章 结构地震反应分析与抗震验算 地面冲击作用后，体系不再受外界任何作用，将做自由振动 V x dt g   根据自由振动位移方程，可得 ( ) sin t g D D e x dt x t t        自由振动初速度为 体系自由振动图 实际的地震地面运动是一 种什么性质的运动？

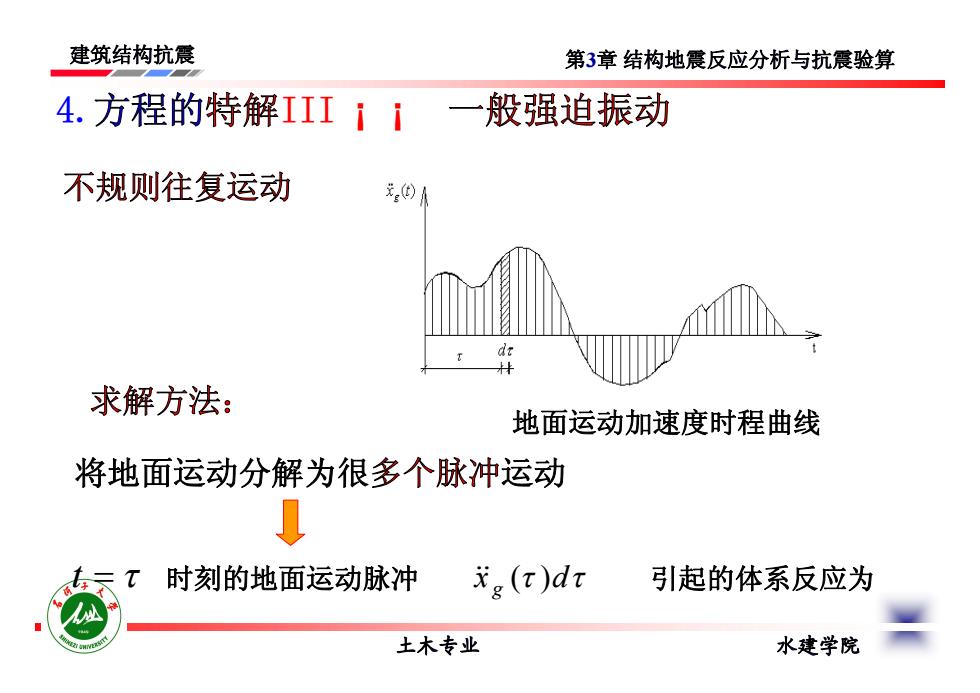
建筑结构抗震 第3章结构地震反应分析与抗震验算 4.方程的特解III11一 般强迫振动 不规则往复运动 元) dt 求解方法： 地面运动加速度时程曲线 将地面运动分解为很多个脉冲运动 时刻的地面运动脉冲 g()dt 引起的体系反应为 土木专业 水建学院

建筑结构抗震 土木专业 水建学院 第3章 结构地震反应分析与抗震验算 不规则往复运动 求解方法： 将地面运动分解为很多个脉冲运动 t   x  d g 时刻的地面运动脉冲  ( ) 4.方程的特解III ¡ ¡ 一般强迫振动 地面运动加速度时程曲线 引起的体系反应为

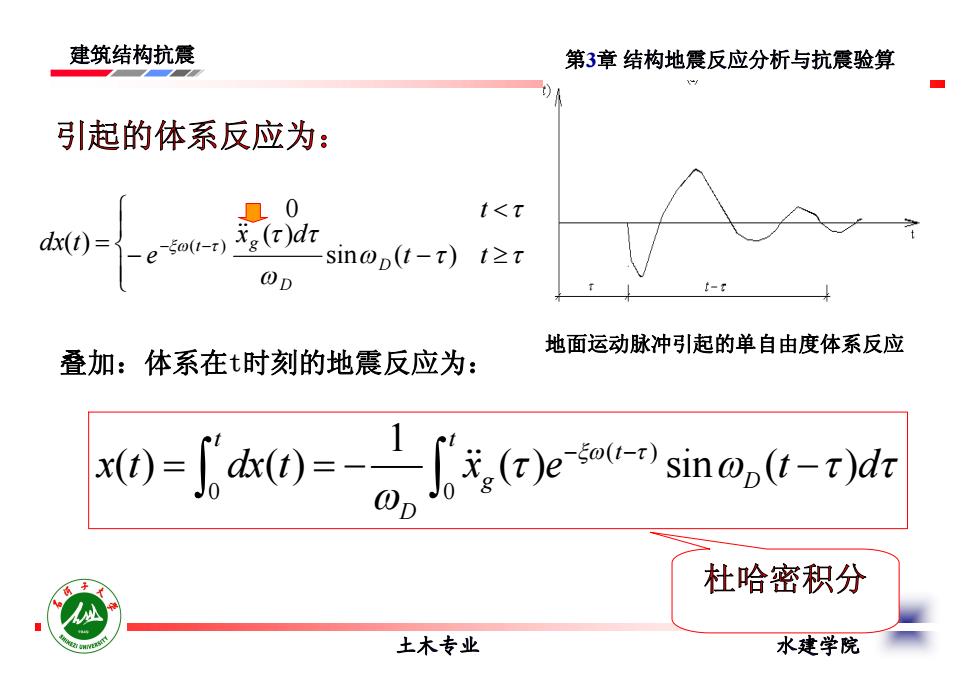
建筑结构抗震 第3章结构地震反应分析与抗震验算 引起的体系反应为： 0 t<T d0=- -5o(1-1) sin@p(t-t)t≥t @p 上=T 地面运动脉冲引起的单自由度体系反应 叠加：体系在t时刻的地震反应为： 0=a0=-心，()sin,-dr 杜哈密积分 土木专业 水建学院

建筑结构抗震 土木专业 水建学院 第3章 结构地震反应分析与抗震验算 引起的体系反应为：                      t t x d e t dx t D D t g sin ( ) ( ) 0 ( ) ( )  叠加：体系在t时刻的地震反应为： ( ) 0 0 1 ( ) ( ) ( ) sin ( ) t t t g D D x t dx t x e t d                 地面运动脉冲引起的单自由度体系反应 杜哈密积分