中国科学技术大学：《计算机视觉》课程教学资源（PPT课件讲稿）第四章 特征的提取与匹配（2/2）边缘以及边特征提取

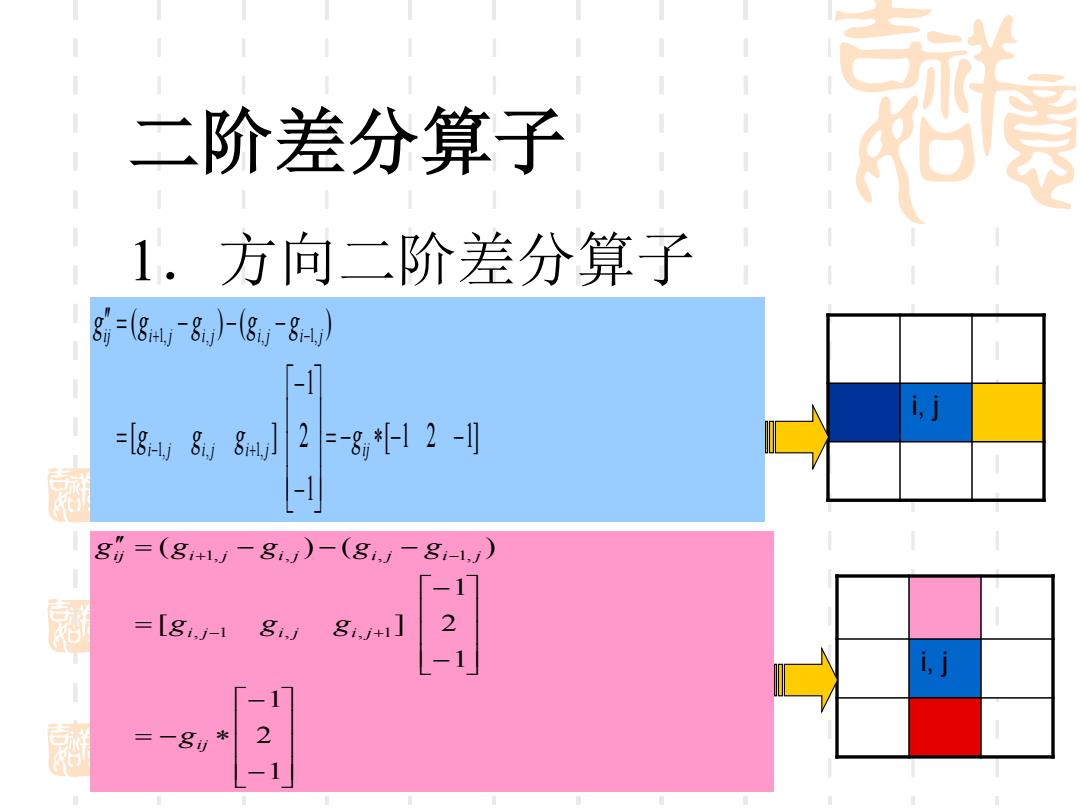
二阶差分算子 1.方向二阶差分算子 888-88） 「- ij =8y884l2F-812- g7=(81+1-8)-（8-8-1） =[sJ18 8+1] =一8

二阶差分算子 1．方向二阶差分算子 [ 1 2 1] 1 2 1 [ ] ( ) ( ) 1, , 1, 1, , , 1, = −  − −           − − =  = − − − − + + − i j i j i j i j i j i j i j i j i j g g g g g g g g g i, j           − − = −            − − =  = − − − − + + − 1 2 1 1 2 1 [ ] ( ) ( ) , 1 , , 1 1, , , 1, i j i j i j i j i j i j i j i j i j g g g g g g g g g i, j

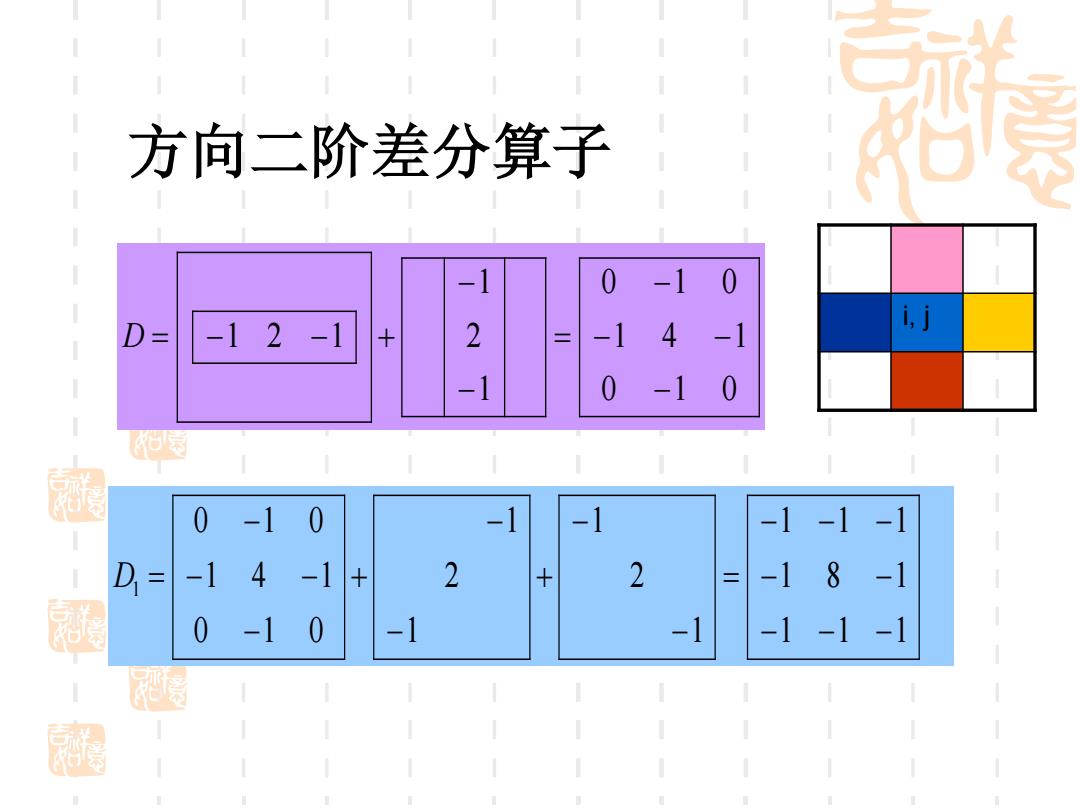
方向二阶差分算子 -1 0 -10 D= -12-1 + 2 -1 4 -1 -1 0 -1 0 0 -10 -1 -1 -1-1-1 D=-14-1 2 + 2 = -18 -1 0-10 -1 -1 -1-1-1

1 1 1 1 8 1 1 1 1 1 2 1 1 2 1 0 1 0 1 4 1 0 1 0 1 − − − − − − − − = − − + − − + − − − − D = 0 1 0 1 4 1 0 1 0 1 2 1 1 2 1 − − − − = − − D = − − + 方向二阶差分算子 i, j

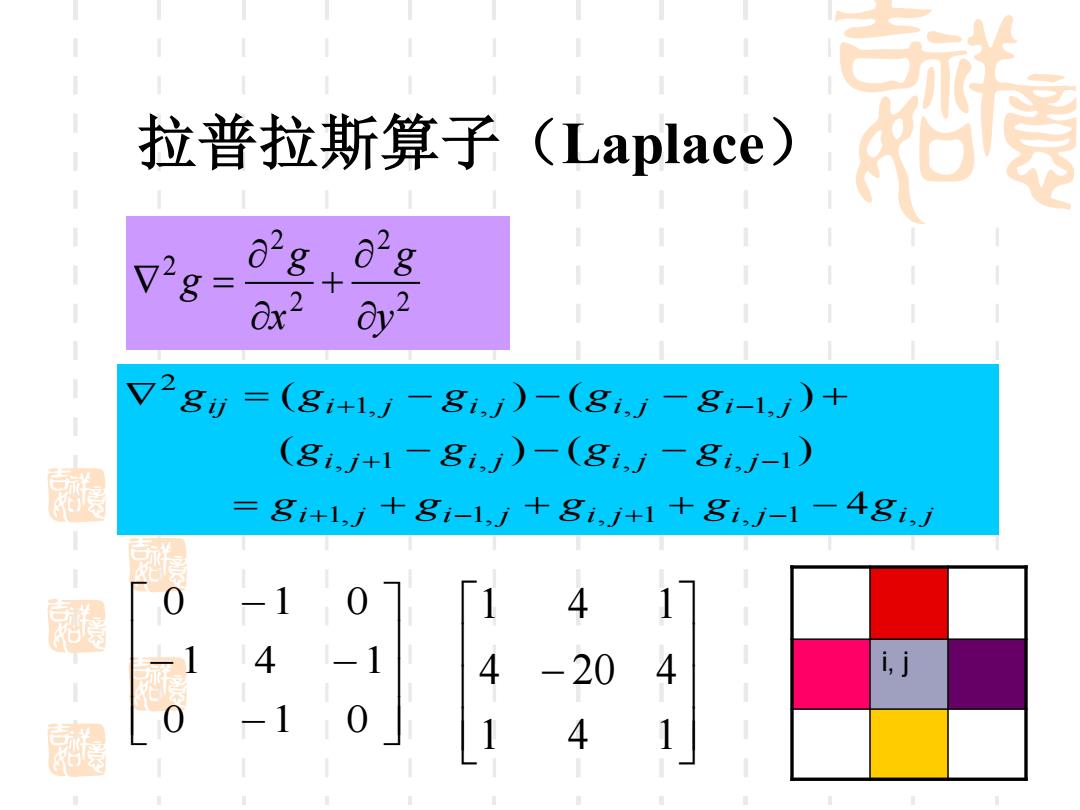
拉普拉斯算子(t.aplace))形 o'g &x2 V2g)=(g1+1,-81,)-（81-81-1）+ (81,+1-81)-(8i,/-8i/-1) = 8i+1,)+81-1+8i,+1+8i,-1-48i, 0 4 1 -1 4 4 20 4 ij 0 1 4 1

拉普拉斯算子（Laplace） 2 2 2 2 2 y g x g g   +    = i j i j i j i j i j i j i j i j i j i j i j i j i j i j g g g g g g g g g g g g g g 1, 1, , 1 , 1 , , 1 , , , 1 1, , , 1, 2 4 ( ) ( ) ( ) ( ) = + + + − − − −  = − − − + + − + − + − + −           − − − − 0 1 0 1 4 1 0 1 0 i, j           − 1 4 1 4 20 4 1 4 1

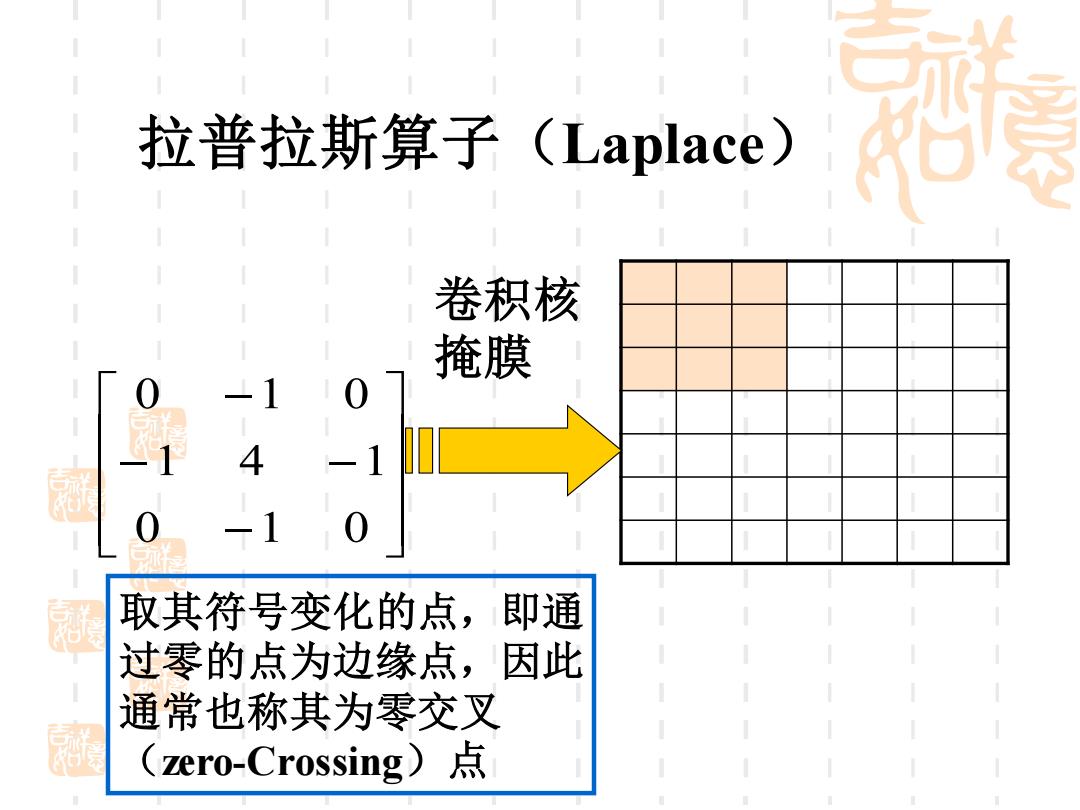
拉普拉斯算子(1.aplace)G 卷积核 掩膜 4 取其符号变化的点，即通 过零的点为边缘点，因此 通常也称其为零交叉 (Zero-Crossing)点

          − − − − 0 1 0 1 4 1 0 1 0 拉普拉斯算子（Laplace） 卷积核 掩膜 取其符号变化的点，即通 过零的点为边缘点，因此 通常也称其为零交叉 （zero-Crossing）点

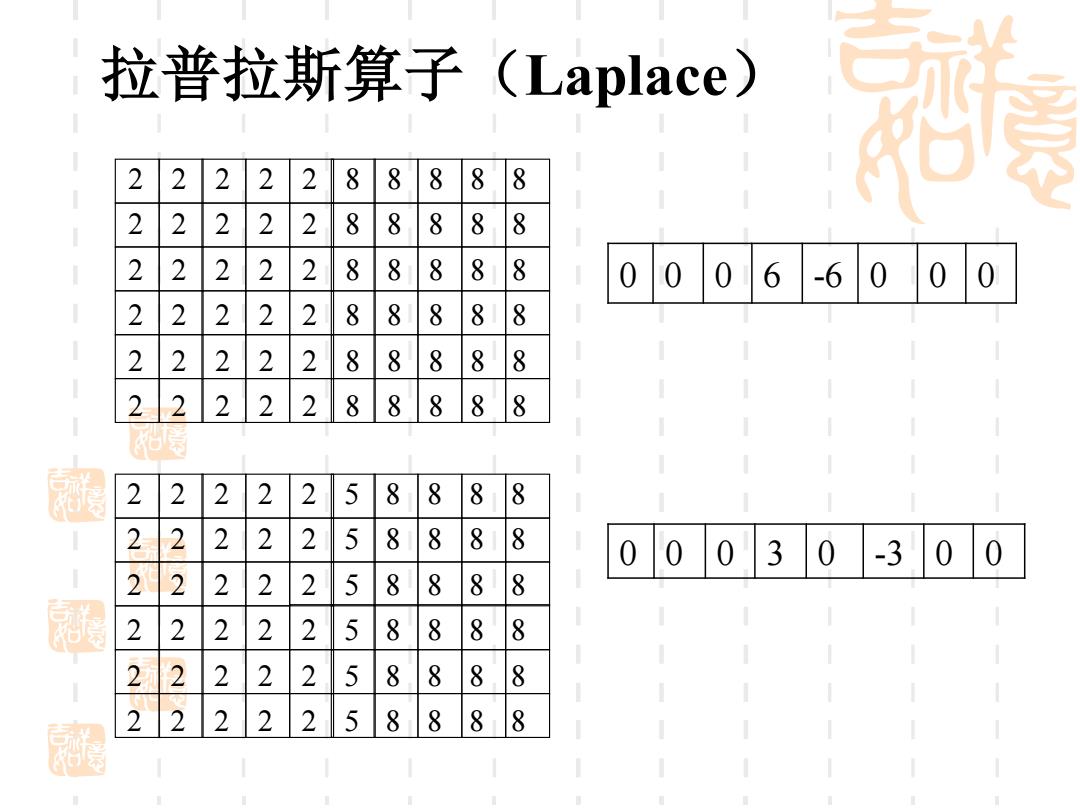
拉普拉斯算子(Laplace) 2 8 8 8 8 8 2 8 8 8 8 8 2 2 8 8 8 8 8 0006-6000 2 2 2 8 8 8 8 8 2 2 2 2 8 8 8 8 8 2 2 2 2 2 8 8 8 8 8 2 2 2 5 8 8 8 8 2 2 2 2 2 5 8 8 81 8 00030-3 0 0 2 2 2 2 2 5 8 8 8 8 2 2 2 2 2 5 8 8 8 8 22 2 2 2 5 8 8 8 8 2 2 5 8 8 88

拉普拉斯算子（Laplace） 2 2 2 2 2 8 8 8 8 8 2 2 2 2 2 8 8 8 8 8 2 2 2 2 2 8 8 8 8 8 2 2 2 2 2 8 8 8 8 8 2 2 2 2 2 8 8 8 8 8 2 2 2 2 2 8 8 8 8 8 0 0 0 6 -6 0 0 0 2 2 2 2 2 5 8 8 8 8 2 2 2 2 2 5 8 8 8 8 2 2 2 2 2 5 8 8 8 8 2 2 2 2 2 5 8 8 8 8 2 2 2 2 2 5 8 8 8 8 2 2 2 2 2 5 8 8 8 8 0 0 0 3 0 -3 0 0