上海交通大学：《高电压工程》课程教学资源_电气工程基础（二）课程导学与习题集

第十五章电力系统过电压 jX cosal+jZsinal 2 o+X。Z Z X P)sinal Z,1/X。 Ko=X,+ZojX jX cosal+jZ sin al 2au号md Z cosal+- -sin al X。 .2cosal+ X ZX2)sinal+cosal+ inal Z cosal+- -sin al =+2 Y)cosal--(元x,Xg (1+ X.)sin al 1 K2= Z cosal+- -sin al X D cosal+- sinal Ko2 =KoIK12=- 1 1+2X)cosal-() (1+ Z Xp -sin al 1 a-字元多md X 对于()可以参照前面几种情况，请广大读者进行分析（结果如下） (d)K2=- 1 (1+ Z s1 cosal-（Z2x)sinal+ 2X。 2Xp 经过上面的讨论，下面通过一道例题将这种分析方法进行详解（解题过程中建议使用三角公 式，尽量避免将大量参数表达为最终结果) 例15-5：下图所示网络，己知，线路：Z=2660,=500km,a=0.06/km,电源：x=102Q, E=289kV,中点电抗器x。=8002,末端电容x=-2000Q,试求： ①U2,U? ②线路电压分布U(x) Xs 1 2 ①- jXp

第十五章 电力系统过电压 8 01 cos sin 2cos ( )sin / / / / cos sin 2cos ( )sin cos sin 2cos ( )sin cos sin cos sin 2 (1 )cos (                    p p eq p p s eq p p s p p p s s p p pp p p s s p p jX l jZ l Z X l l Z jX X Z K jX l jZ l jX Z jX jX Z X l l X Z Z l l X X X Z Z X l ll l X XX Z X Z l l X X X Z l X ZX                 2  )sin s p ZX l X  12 1 cos sin p K Z l l X     02 01 12 2 2 cos sin 1 2 (1 )cos ( )sin cos sin 1 2 (1 )cos ( )sin            p s ss p pp p s ss p pp Z l l X K KK X X ZX Z Z l l l l X ZX X X X X ZX Z l l X ZX X         对于（d）可以参照前面几种情况，请广大读者进行分析（结果如下） （d） 02 1 (1 )cos ( )sin 2 22 s s s p pp K X X X Z l l X ZX X       经过上面的讨论，下面通过一道例题将这种分析方法进行详解（解题过程中建议使用三角公 式，尽量避免将大量参数表达为最终结果） 例 15-5：下图所示网络，已知，线路：Z＝266Ω，l=500km，α＝0.06o /km，电源：jxs=j102Ω， E=289kV，中点电抗器 jxp=j800Ω,末端电容 jxC=-j2000Ω,试求： ①U2，U1? ②线路电压分布 U(x)

第十五章电力系统过电压 9 图15-10例15-5 题解：本题目中存在4个端点，即发电机出口0、线路出线端1、线路中点m和线路末端2：同时 线路末端接入了电容器，并不是常见的电抗器，对此可以将电容器认为是负的电抗器。 (1)这样m-2之间与前面讨论(a)情况的是相似的，即 8=g1又=g12600=-758” -X。 cos(-7.58) Km2= =1.074 U cos( 28) cos(0.06×250+7.58) (2)m点之后的线路等效为电容（如果计算为正值，则为等效电抗器），该电容与电抗器并联 形成等效电抗器X。,这样0-m之间与前面讨论(a)情况的完全相同的，根据前面(a) 讨论的情况可以计算出Ka、Ka, X,×[-2agg-8】 X,= ,-g号-Q)） =-j800×266cg006×250+758）=-J3191.270 800-266ctg(0.06×250+7.58) 中=g少=g02 =21° 266 8=g之、 0=g-13827=-4.76° c0s21°c0s(-4.76) -=1.23 E c0s0+4-9,)cos(2r+0.06x250+4.76) 2 -0) Kol=- co) c0s2I(0.06x250+4.76）=1.16 E c0s(21°+0.06×250+4.76) .U=KE=1.16×289=335.23kp U2=KmKm2E=1.23×1.074×289=381.77kP 2)根据电压分布特性，易得：

第十五章 电力系统过电压 9 图 15-10 例 15-5 题解：本题目中存在 4 个端点，即发电机出口 0、线路出线端 1、线路中点 m 和线路末端 2；同时 线路末端接入了电容器，并不是常见的电抗器，对此可以将电容器认为是负的电抗器。 （1）这样 m-2 之间与前面讨论（a）情况的是相似的，即 1 1 1 266 7.58 2000 C Z tg tg X          2 1 2 1 cos cos( 7.58 ) 1.074 cos(0.06 250 7.58 ) cos( ) 2 m m U K U l             （2）m 点之后的线路等效为电容（如果计算为正值，则为等效电抗器），该电容与电抗器并联 形成等效电抗器 ' P jX ，这样 0-m 之间与前面讨论（a）情况的完全相同的，根据前面（a） 讨论的情况可以计算出 K0m、K01 1 ' 1 [ ( )] 2 ( ) 2 800 266 (0.06 250 7.58 ) 3191.27 800 266 (0.06 250 7.58 ) P P P l jX jZctg jX l jX jZctg j ctg j ctg                    1 1 102 21 266 XS tg tg Z       1 1 2 ' 266 4.76 3191.27 P Z tg tg X         2 2 cos cos cos 21 cos( 4.76 ) 1.23 cos(21 0.06 250 4.76 ) cos( ) 2 m om U K E l                  2 1 1 2 cos cos( ) cos 21 (0.06 250 4.76 ) 2 1.16 cos(21 0.06 250 4.76 ) cos( ) 2 o l U K E l                     1 1 1.16 289 335.23 U K E kV    o 2 2 1.23 1.074 289 381.77 U K K E kV    om m 2）根据电压分布特性，易得：

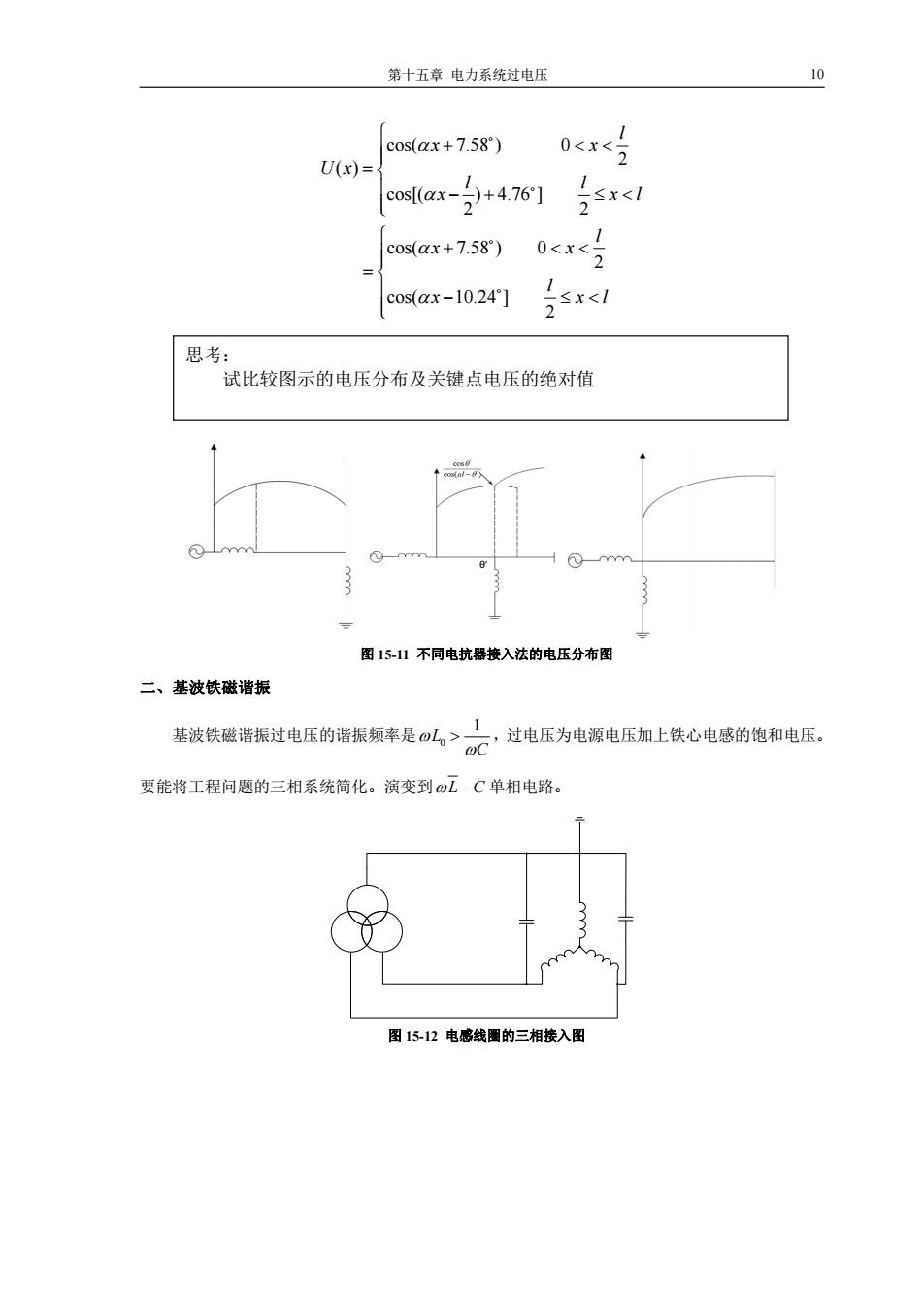
第十五章电力系统过电压 10 cos(ax+7.58) 0<x 1 U(x)= coax--2+4.76] 1 ≤x<l cos(ax+7.58) 0<x<2 cos(ax-10.24] ≤x<l 思考： 试比较图示的电压分布及关键点电压的绝对值 cosal-8y 图15-11不同电抗器接入法的电压分布图 二、基波铁磁谐振 基波铁磁谐振过电压的谐振频率是⊙L。> ,过电压为电源电压加上铁心电感的饱和电压。 要能将工程问题的三相系统简化。演变到oL-C单相电路。 图1512电感线圈的三相接入图

第十五章 电力系统过电压 10 cos( 7.58 ) 0 2 ( ) cos[( ) 4.76 ] 2 2 cos( 7.58 ) 0 2 cos( 10.24 ] 2 l x x U x l l x x l l x x l x xl                              图 15-11 不同电抗器接入法的电压分布图 二、基波铁磁谐振 基波铁磁谐振过电压的谐振频率是 0 1 L C    ，过电压为电源电压加上铁心电感的饱和电压。 要能将工程问题的三相系统简化。演变到L C 单相电路。 图 15-12 电感线圈的三相接入图 思考： 试比较图示的电压分布及关键点电压的绝对值

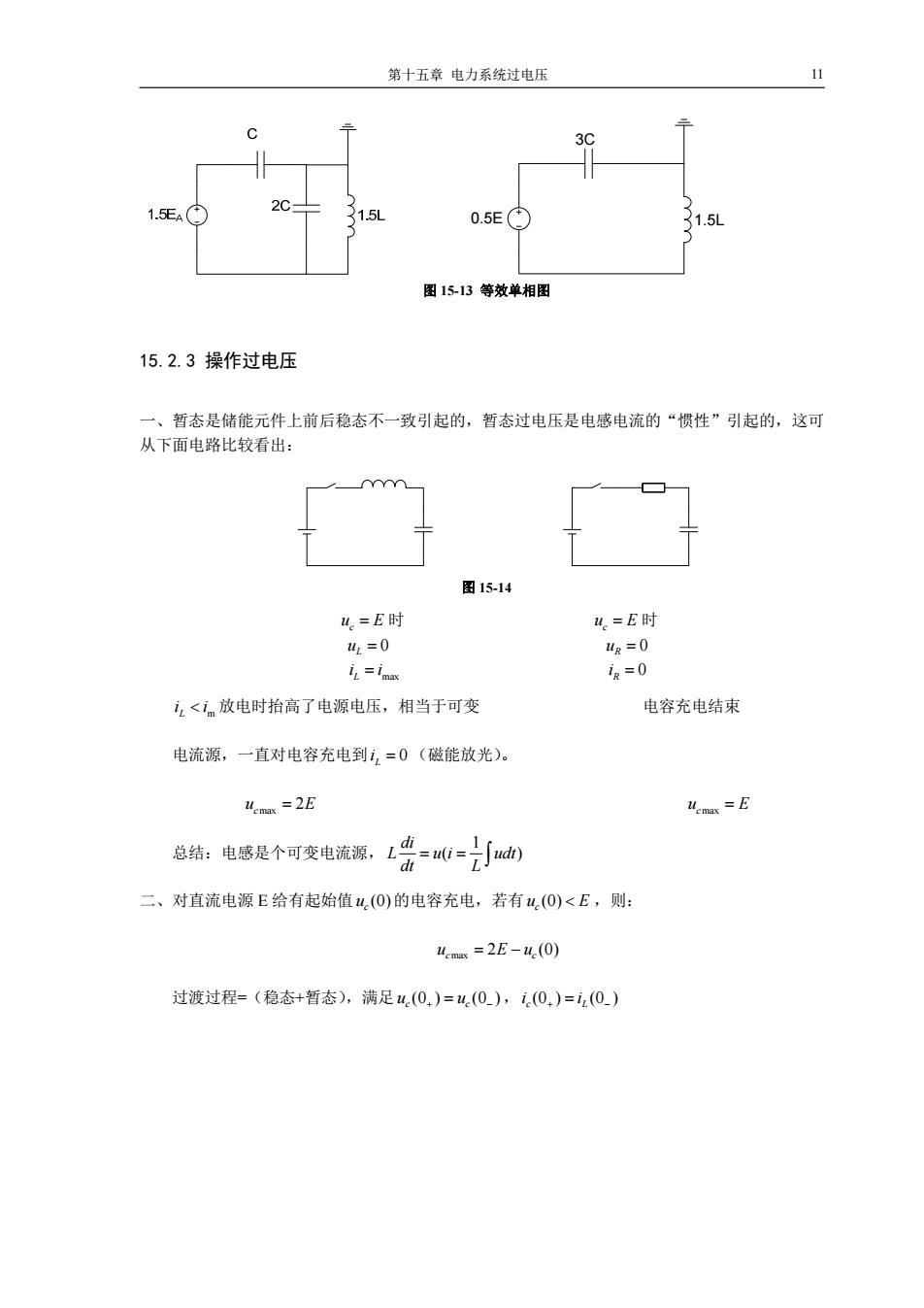
第十五章电力系统过电压 11 3C 1.5EA 15L 0.5E 1.5L 图1513等效单相图 15.2.3操作过电压 一、暂态是储能元件上前后稳态不一致引起的，暂态过电压是电感电流的“惯性”引起的，这可 从下面电路比较看出： 图15-14 。=E时 4。=E时 4z=0 4R=0 iL =imax e=0 iz<im放电时抬高了电源电压，相当于可变 电容充电结束 电流源，一直对电容充电到1，=0（磁能放光）。 Vemax =2E uemax =E 总结：电感是个可变电流源，告=d) 二、对直流电源E给有起始值w,(O)的电容充电，若有4，(O)<E,则： uemax =2E-u(0) 过渡过程=（稳态+暂态），满足u.(0,)=4.(0),i(0,)=iz(0)

第十五章 电力系统过电压 11 0.5E 1.5L 3C 图 15-13 等效单相图 15.2.3 操作过电压 一、暂态是储能元件上前后稳态不一致引起的，暂态过电压是电感电流的“惯性”引起的，这可 从下面电路比较看出： 图 15-14 c u E  时 c u E  时 0 L u  0 R u  L max i i  0 Ri  L m i i  放电时抬高了电源电压，相当于可变 电容充电结束 电流源，一直对电容充电到 0 Li  （磁能放光）。 max 2 c u E  cmax u E  总结：电感是个可变电流源， 1 ( ) di L u i udt dt L    二、对直流电源 E 给有起始值 (0) c u 的电容充电，若有 (0) c u E  ，则： max 2 (0) c c u Eu   过渡过程=（稳态+暂态），满足 (0 ) (0 ) c c u u    ， (0 ) (0 ) c L i i   

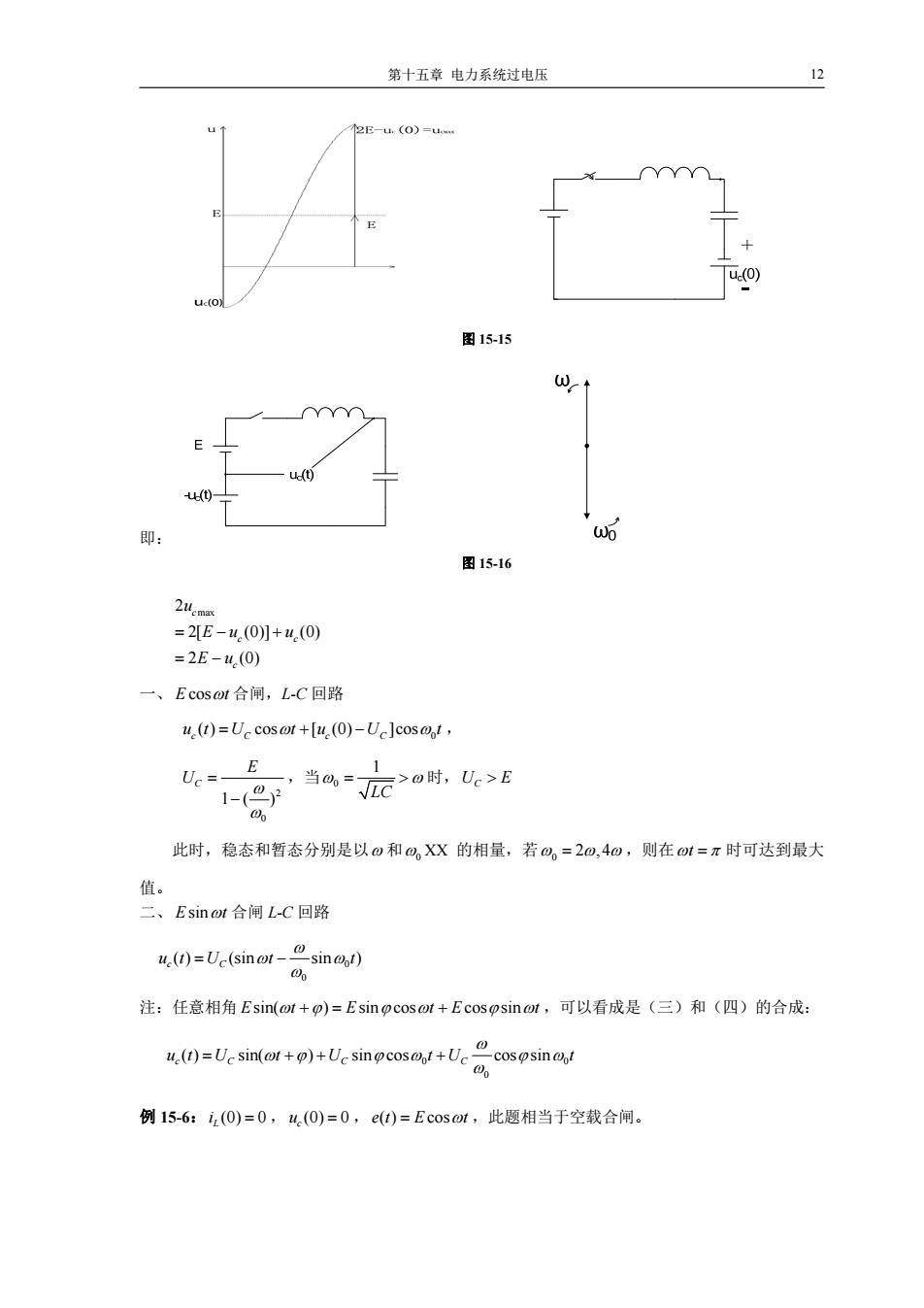
第十五章电力系统过电压 12 2E-u(O)=uw… u(0) ue(O) 图15-15 u(t) () 即： 图15-16 2uemax =2[E-u(0]+u(0) =2E-u.(0) 一、E cos@t合闸，L-C回路 u(t)=Uccosot+[u(0)-Uc]cos@t, E 1 Uc= 1-(⊙2 当o=√C >o时，Uc>E 00 此时，稳态和暂态分别是以0和，XX的相量，若0。=20,4o,则在t=π时可达到最大 值。 二、Esin@t合闸L-C回路 u.(1)=Uc(sinot- 一s1n0t) 注：任意相角Esin(at+p)=Esinpcosot+Ecososinot,可以看成是（三）和（四）的合成： u(1)=Ucsin(+)+Uesinpcosl+Uccospsino! 00 例15-6：iz(0)=0,4,(0)=0,e(t)=Ecos@t,此题相当于空载合闸

第十五章 电力系统过电压 12 图 15-15 即： 图 15-16 max 2 2[ (0)] (0) 2 (0) c c c c u Eu u E u     一、 E cost 合闸，L-C 回路 0 ( ) cos [ (0) ]cos cC c C ut U t u U t     ， 2 0 1( ) C E U     ，当 0 1 LC    时，U E C  此时，稳态和暂态分别是以 和0 XX 的相量，若 0   2 ,4   ，则在t   时可达到最大 值。 二、 Esint 合闸 L-C 回路 0 0 ( ) (sin sin ) c C ut U t t       注：任意相角 Esin( ) sin cos cos sin t E tE t       ，可以看成是（三）和（四）的合成： 0 0 0 ( ) sin( ) sin cos cos sin cC C C ut U t U t U t          例 15-6： (0) 0 Li  ， (0) 0 c u  ，et E t ( ) cos   ，此题相当于空载合闸