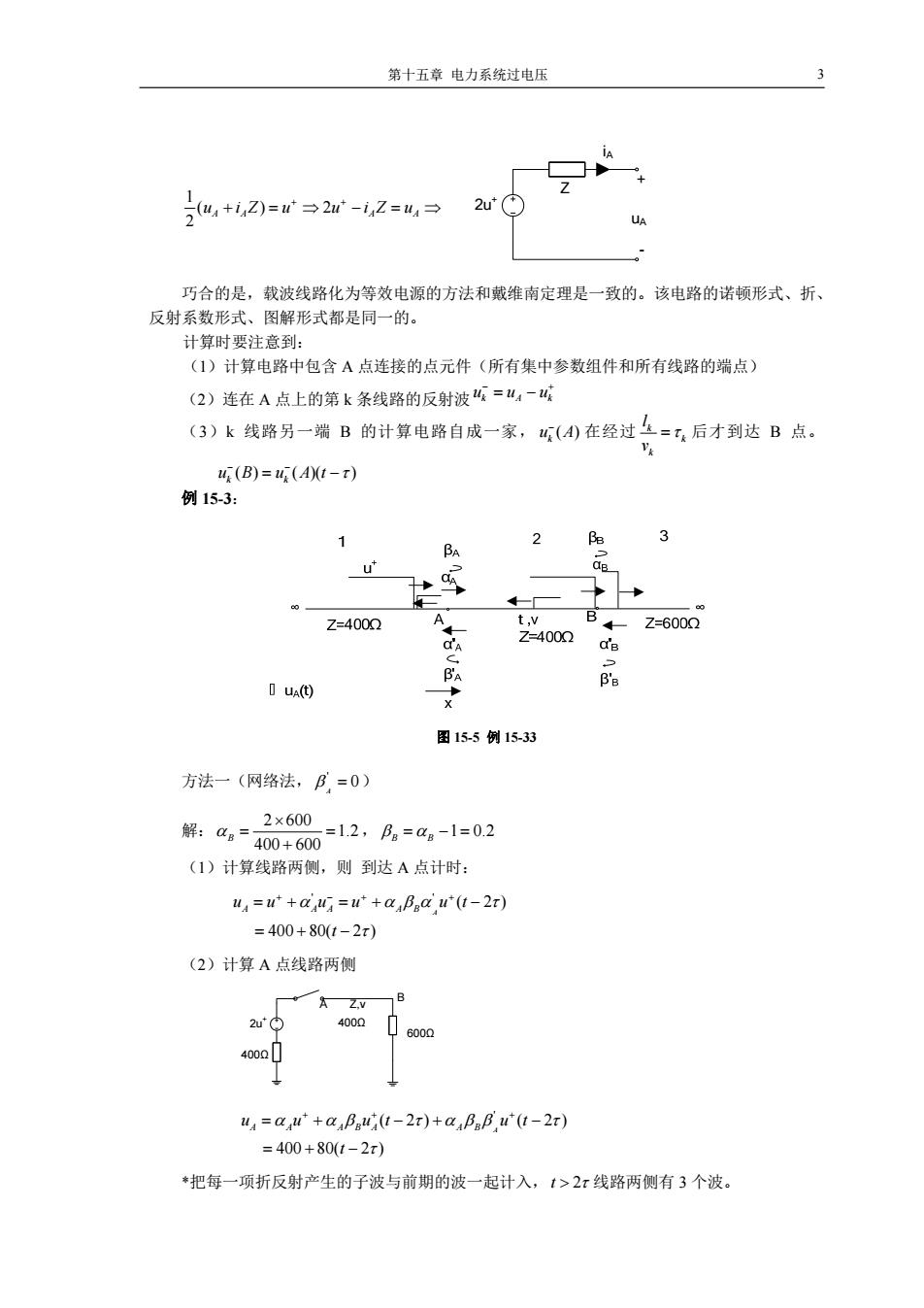
第十五章电力系统过电压 u,+i2=r→2-i2=,3 2u UA 巧合的是,载波线路化为等效电源的方法和戴维南定理是一致的。该电路的诺顿形式、折、 反射系数形式、图解形式都是同一的。 计算时要注意到: (1)计算电路中包含A点连接的点元件(所有集中参数组件和所有线路的端点) (2)连在A点上的第k条线路的反射波“=4- (3)k线路另一端B的计算电路自成一家,(4在经过生=t,后才到达B点。 4(B)=4(A)t-t) 例15-3: 2 阳 BA u 60 Z=4002 t,v B Z=6002 CIA Z-4002 c'e BA DUA(t) B'e X 图15-5例15-33 方法一(网络法,阝,=0) 2×600 解:g=400+600 12,B。=aa-1=02 (1)计算线路两侧,则到达A点计时: u=u+au=u'+a Bea u'(1-27) =400+80(t-2x) (2)计算A点线路两侧 2u0 400 6000 4000 u4=a4+aaBg(t-2r)+a4Ba阝(t-2r) =400+80(t-2x) *把每一项折反射产生的子波与前期的波一起计入,1>2π线路两侧有3个波
第十五章 电力系统过电压 3 2u+ Z iA + - uA 巧合的是,载波线路化为等效电源的方法和戴维南定理是一致的。该电路的诺顿形式、折、 反射系数形式、图解形式都是同一的。 计算时要注意到: (1)计算电路中包含 A 点连接的点元件(所有集中参数组件和所有线路的端点) (2)连在 A 点上的第 k 条线路的反射波 k Ak uuu (3)k 线路另一端 B 的计算电路自成一家, ( ) k u A 在经过 k k k l v 后才到达 B 点。 ( ) ( )( ) k k u B u At 例 15-3: 图 15-5 例 15-33 方法一(网络法, ' 0 A ) 解: 2 600 1.2 400 600 B , 1 0.2 B B (1)计算线路两侧,则 到达 A 点计时: ' ' ( 2) 400 80( 2 ) A AA A B A u u u u ut t (2)计算 A 点线路两侧 2u+ A Z,v B 600Ω 400Ω 400Ω ' ( 2) ( 2) 400 80( 2 ) A A A BA A B A u u ut ut t *把每一项折反射产生的子波与前期的波一起计入,t 2 线路两侧有 3 个波。 1 ()2 2 AA A A u iZ u u iZ u

第十五章电力系统过电压 4 方法二 (1)同方法一 (2)计算t≥2x时,A点电压 44=801(t-2x) u4=4801(t-2r) 4=uA-=4001(t-2x) 2u=800 2iA=160(tT) *只承认每条线路上有一个前行波和一个反行波。 图15-6例3 15.2.2稳态过电压 一、长线容升效应 电感一电容效应发生于L-C串联支路的工频阻抗为容性的电路。空载长线的电位升高是一种 从线路首端到末端的积累的电感一电容效应。线路的电压分布呈余弦函数。首端入口阻抗呈容性 (al<90°),关于线路电抗器: (1)线路末端的电抗器(一般x。>Zctgal)使线路首端输入阻抗变大,i=0点从末端前移至 (0=g乙),线路最大电压降L降为 1 a cosal os(al-0) (2)线路中点的电抗器与该点后的线路入口阻抗并联值大于线路入口阻抗,有与(1)有相似的 效果: (3)线路首端的电抗器与线路入口阻抗并联值大于线路入口阻抗(若x。>Zctgal),从电源看 来“线路变短”,母线的电位升高下降。 例15-4:如下图所示,Z>Z2,M>2,计算比较,说明原因,哪头合闸过电压较高? Z1,1 图15-7例15-4
第十五章 电力系统过电压 4 方法二 (1)同方法一 (2)计算t 2 时,A 点电压 80 ( 2 ) A u It 480 ( 2 ) A u It 400 ( 2 ) AAA u u u It *只承认每条线路上有一个前行波和一个反行波。 图 15-6 例 3 15.2.2 稳态过电压 一、长线容升效应 电感—电容效应发生于 L-C 串联支路的工频阻抗为容性的电路。空载长线的电位升高是一种 从线路首端到末端的积累的电感—电容效应。线路的电压分布呈余弦函数。首端入口阻抗呈容性 ( 90o al ),关于线路电抗器: (1)线路末端的电抗器(一般 c p x Z tgal )使线路首端输入阻抗变大,i=0 点从末端前移至 ( ) p Z tg a x ,线路最大电压降 1 cos al 降为 1 cos( ) al (2)线路中点的电抗器与该点后的线路入口阻抗并联值大于线路入口阻抗,有与(1)有相似的 效果; (3)线路首端的电抗器与线路入口阻抗并联值大于线路入口阻抗(若 c p x Z tgal ),从电源看 来“线路变短”,母线的电位升高下降。 例 15-4:如下图所示, 1 21 2 Z Z , ,计算比较,说明原因,哪头合闸过电压较高? 图 15-7 例 15-4

第十五章电力系统过电压 5 ⊙+ -jZ2ctg(al/2) 图15-8例15-4等效图 左侧大,前电感大,后电容大。 讨论:以下四种线路首末端电压比 E。X1 Z,a,I 2 E。X, Z,a,I 2 @W一 jXp (a) (b) E。X1 Z a,1 Z,a,1 (c) (d) 图15-9电抗器不同接入方法图 对于此类问题的讨论,都是基于线路12的端口电压、电流方程的讨论,下面可以针对以上四 种情况进行分析 U=U,cosal+jl Zsinal (1) 1、对于(a图,端日2有如下关系:U,=X,,即 U2, 将此结果带入上面的端口电 压方程,可以得到线路12端点电压方程: U=U,(cosal+j- Z -sin al) (2) 1 即可得到线路12端点电压比K2= (3) cosal+- -sin al X 下面研究发电机端口0到线路端口1的电压情况,将I2= 代入上面的端口电流方程, X
第十五章 电力系统过电压 5 图 15-8 例 15-4 等效图 左侧大,前电感大,后电容大。 讨论:以下四种线路首末端电压比 E0 s jX p jX E0 s jX p jX (a) (b) E0 s jX p jX p jX E0 s jX p jX (c) (d) 图 15-9 电抗器不同接入方法图 对于此类问题的讨论,都是基于线路 12 的端口电压、电流方程的讨论,下面可以针对以上四 种情况进行分析 12 2 2 1 2 cos sin sin cos U U l jI Z l U I j lI l Z (1) 1、 对于(a)图,端口 2 有如下关系:U jX I 2 2 p ,即 2 2 p U I jX ,将此结果带入上面的端口电 压方程,可以得到线路 12 端点电压方程: 1 2 (cos sin ) p Z U U lj l jX (2) 即可得到线路 12 端点电压比 12 1 cos sin p K Z l l X (3) 下面研究发电机端口 0 到线路端口 1 的电压情况,将 2 2 p U I jX 代入上面的端口电流方程

第十五章电力系统过电压 6 1 I.=0;(jsinal+ -cos al) (4) X。 式(2)除以式(4),可得: Z cosal+ sinal X。 1、 1 1 sinal+ -cosal X (5) 对于发电机端口0到线路端口1的电压,根据串联电路的分压原理,易得: Za Ko=Z,+Zo (6) 将式(5)代入式(6),可以得到: Z cosal + -sin al sin al+ 1 cosal cosal+Zsinal jX。 X Kol=- (7) cosal+- -sin al (1+ Z.)cosal+( ZZ:)sin al j,+1 D 。Z cosal jXp 那么K2=K1K2,即式(7)×式(3): cosal+- 1 X- (1+ X。 ()sinal cosal+sinal 对上式进行化简,可得K2=一 1 )cosal+( (1+ X X.)sinal .Z 2、(b)相对于(a)情况简单一些,因为线路12是一条空载线路,那么k2很容易通过教材上 cosal'乙-jzcosal 的公式得到K,=1 sinal 对于发电机出口0到线路端点1形成的集中参数等效电路如下图所示:
第十五章 电力系统过电压 6 1 2 1 1 ( sin cos ) p I Uj l l Z jX (4) 式(2)除以式(4),可得: 1 1 cos sin 1 1 sin cos p eq p Z l l U X Z I jl l Z jX (5) 对于发电机端口 0 到线路端口 1 的电压,根据串联电路的分压原理,易得: 01 eq s eq Z K Z Z (6) 将式(5)代入式(6),可以得到: 01 cos sin 1 1 sin cos cos sin cos sin (1 )cos ( )sin 1 1 sin cos p p p s s p p p s p Z l l X Z jl l l l Z jX X K ZZ Z Z l l l l X X XZ jZ jl l Z jX (7) 那么 K KK 02 01 12 ,即式(7)×式(3): cos sin 1 (1 )cos ( )sin cos sin p s s p p p Z l l X ZZ Z Z l l l l X XZ X 对上式进行化简,可得 02 1 (1 )cos ( )sin s ss p p K X XX l l X XZ 2、 (b)相对于(a)情况简单一些,因为线路 12 是一条空载线路,那么 k12 很容易通过教材上 的公式得到 12 1 cos K l , cos sin eq l Z jZ l 对于发电机出口 0 到线路端点 1 形成的集中参数等效电路如下图所示:
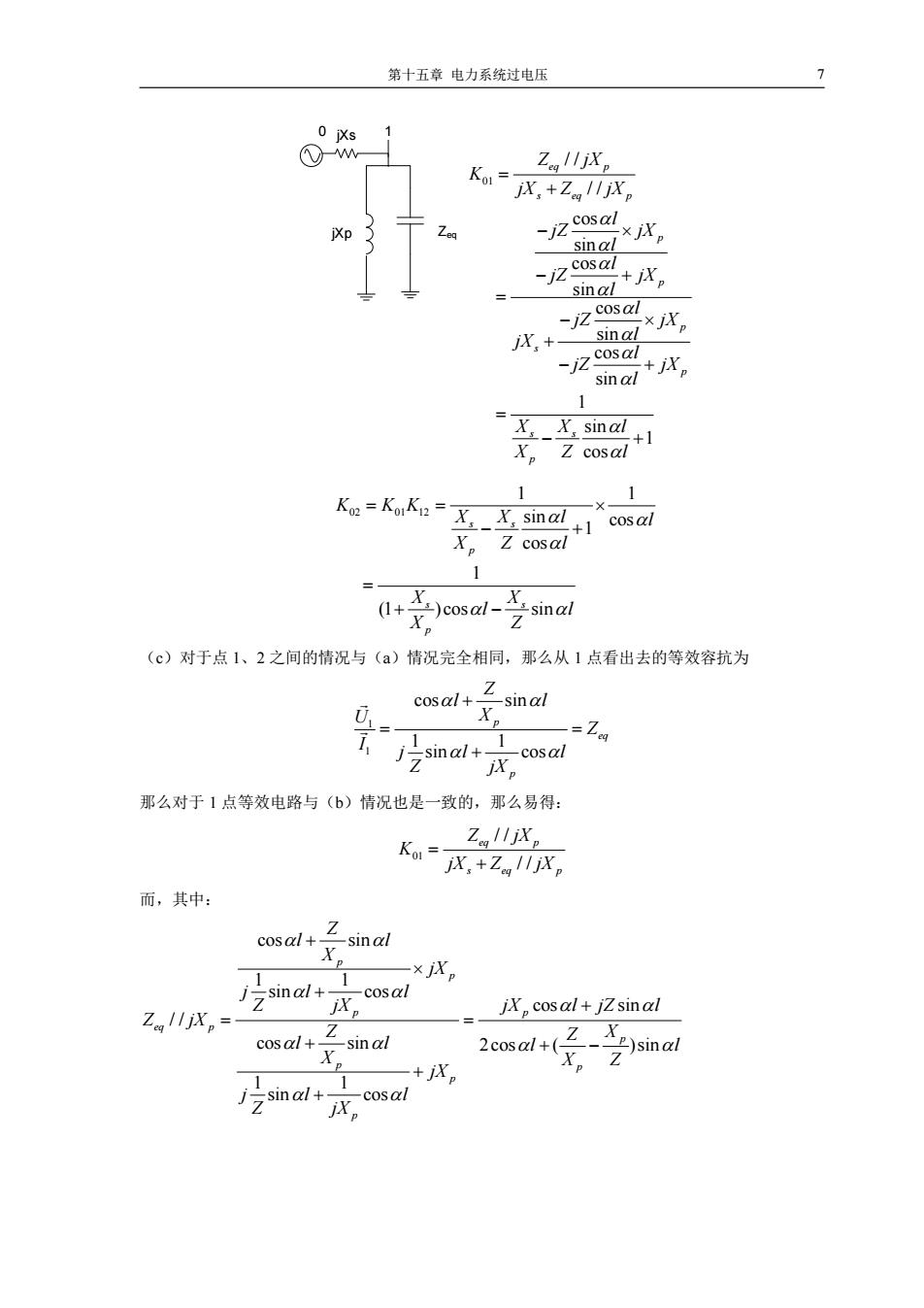
第十五章电力系统过电压 7 0 Xs 1 Ko=- Zg1X。 X,+Zg11jX。 18 -jz cosal sinal jⅸp -jz cosal jXp sinal -jz cosal jXp iX,+sinal -iz cosal sinal +jXp 1 X.X.sinal +1 X。Z cosal 1 1 KKok:=XY.sinal+cosal Xp Z cosal 1 X.)cosal- (1+ .sinal (c)对于点1、2之间的情况与(a)情况完全相同,那么从1点看出去的等效容抗为 cosal+- -sin al 1、 1 -La -cosal 出 那么对于1点等效电路与(b)情况也是一致的,那么易得: Zg11X。 Km=X,+乙11jXp 而,其中: Z cosal+ sinal Xp 1 1 一×X。 inal+ cosal ZcglljXp= X。 jXp cosal+jZsinal cosal+- 1 -sin al 2cosal+(- Z Y )sinal cos sinal+-1
第十五章 电力系统过电压 7 jXs 1 jXp Zeq 0 01 / / / / cos sin cos sin cos sin cos sin 1 sin 1 cos eq p s eq p p p p s p s s p Z jX K jX Z jX l jZ jX l l jZ jX l l jZ jX l jX l jZ jX l X X l XZ l 02 01 12 1 1 sin cos 1 cos 1 (1 )cos sin s s p s s p K KK X X l l XZ l X X l l X Z (c)对于点 1、2 之间的情况与(a)情况完全相同,那么从 1 点看出去的等效容抗为 1 1 cos sin 1 1 sin cos p eq p Z l l U X Z I jl l Z jX 那么对于 1 点等效电路与(b)情况也是一致的,那么易得: 01 / / / / eq p s eq p Z jX K jX Z jX 而,其中: cos sin 1 1 sin cos cos sin / / cos sin 2cos ( )sin 1 1 sin cos p p p p eq p p p p p p Z l l X jX jl l Z jX jX l jZ l Z jX Z X Z l l l l X X Z jX jl l Z jX