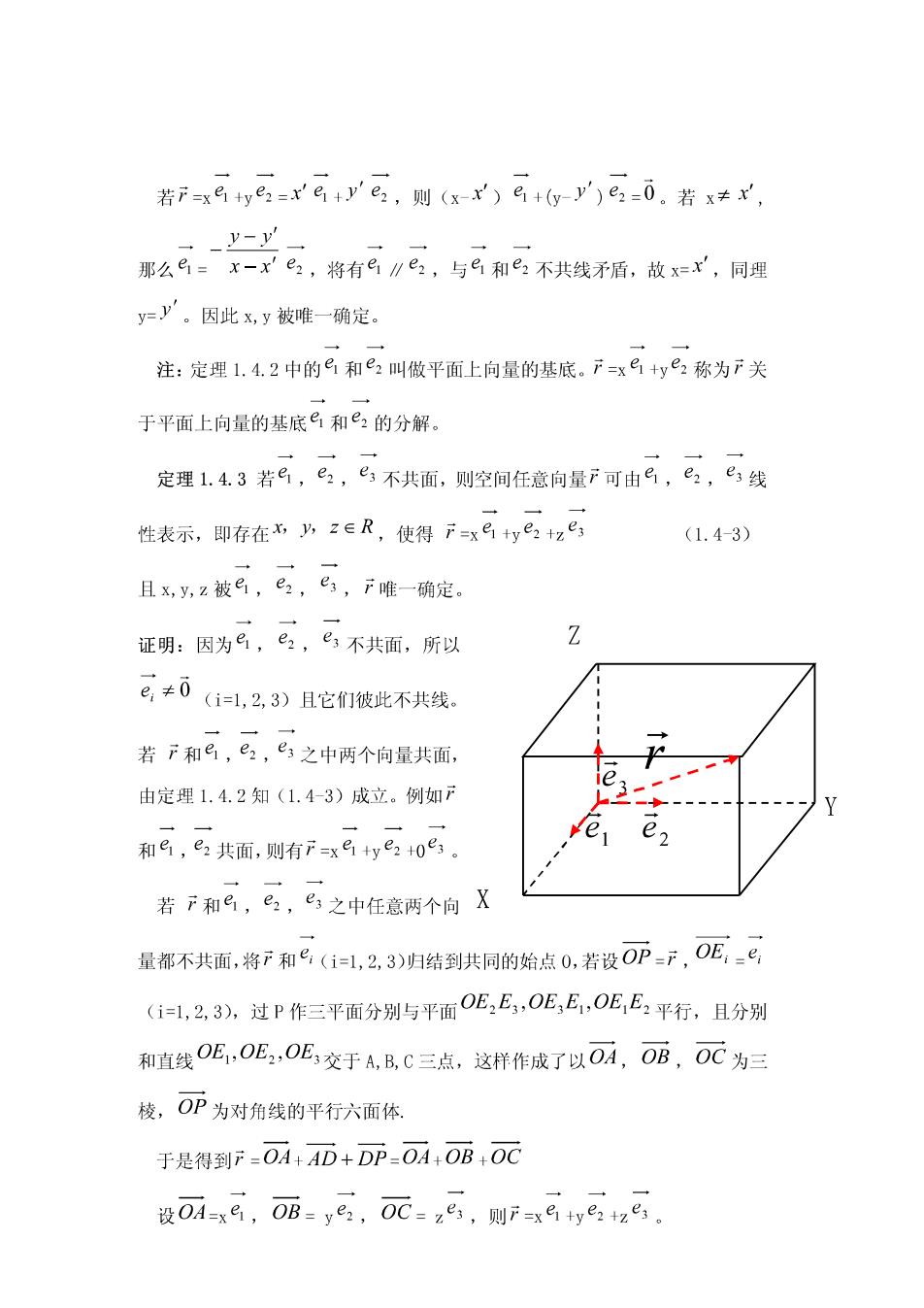
若F=x%+ye2=x'e+y'e2,则(xx')%+y-y')e2=0。若x≠x, -y-y' 那么8=x-x'e,将有e∥e,与e和e2不共线矛盾,故x=x',同理 y=y。因此x,y被唯一确定。 注:定理1.4.2中的e和e2叫做平面上向量的基底。下=xe+ye2称为下关 于平面上向量的基底9和e2的分解。 定理1.4.3若e,e,e不共面,则空间任意向量F可由e,e2,e线 性表示,即存在,少z∈R,使得下=x%ye2+ze (1.4-3) 且x,,z被,e2,e,F唯一确定。 证明:因为,,e不共面,所以 Z e,≠0(i=,23)且它们彼此不共线. 若F和,e2,e之中两个向量共面, 由定理1.4.2知(1.4-3)成立。例如F 3 → 和8,e2共面,则有F=xe+ye2+0e3。 e2 若F和e,e,e之中任意两个向X 量都不共面,将F和e(i1,2,3)归结到共同的始点0,若设0P=元,0E,=8, (i1,2,3),过P作三平面分别与平面OE,E,OE,E,OEE,平行,且分别 和直线OE,OE2,OE交于A,B,C三点,这样作成了以OA,OB,,OC为三 棱,OP为对角线的平行六面体. 于是得到F=-OA+AD+DP=OA+OB+OC 设OA=x,0B=ye,0C=z8,则F=x8+yP+2e

下证唯一性。若产=x巴+y2+2=x日+y'e2+ze,那么 (x-x')e+y-y')e2+z-z')e3-0 若x≠x,则 e=x-x' x-xre 椐定理1.4.2知9,e2,e共面,与e,e,,e不共面矛盾。故x=x', 同理可证y=少,x2'。因此x,y,z被,2,e,产唯一确定。 注:定理1.4,3中的9,e2,e叫做空面上向量的基底,F=xe+ye2+ze 称为F关于平面上向量的基底9和e2,e3的分解。 例1已知△0AB,其中OA=石,OB=b,M,N分别是0A,OB上的点,且 OM=乙石,ON=“b,其中0<1<”,设AN,M与相交于P,试把OP=D 分解成云,b的线性组合。 少 b 0 M 解:因p=OM+MP,OM=元a,而由定理1.4.1知存在m∈R,使得 MP=mMB=m(OB-OM)=m(b-4b), 于是 p=aa+m(B-AB)=4(1-m)=mb (1) 另一方面, p=ON:NP=b+nNA=b+n(OA-ON)=ub+na-ub)=na+m-n)b (2)