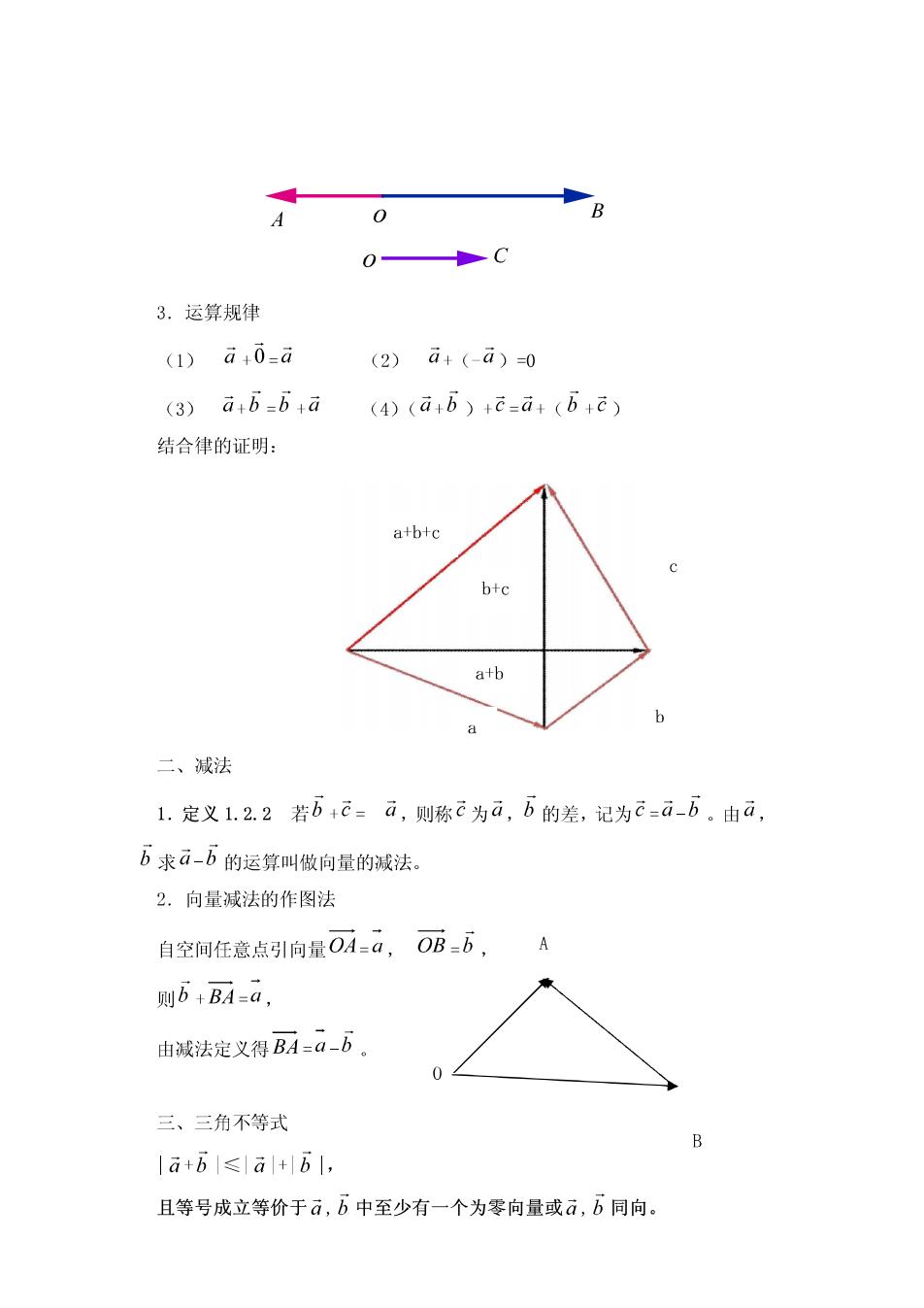
B 0 3.运算规律 (1) a+0=d (2)ā+(-ā)=0 (3) ab-ba (4)(a+b)+c=a+(b+c) 结合律的证明: a+b+c b+c a+b b 二、减法 1.定义1.2.2若b+c=d,则称c为d,b的差,记为c=d-b。由a, b求-b的运算叫做向量的减法。 2.向量减法的作图法 自空间任意点引向量OA=a, OB=b A 则b+BA=a, 由减法定义得BA=a-b。 0 三、三角不等式 B |ā+b≤a+b, 且等号成立等价于ā,b中至少有一个为零向量或ā,b同向

四、例题 例1:设a,b,c不共线,则它们顺次终点与始点相连成一个三角形的 充分必要条件是a+b+c-0 证明:必要性 设a,万,c可构成三角形ABC(图),且 AB=a,BC=b,CA=c,那么AB+BC+CA=AA=0,即a+b+c=0。 B 充分性设a+b+c=-0(如图), 作AB=a,BC-b, 那么AC=a+b,于是AC+c-0, 因此c=-AC=CA,故a,b,c可构成三角形ABC。 例2用向量方法证明:对角线互相平分的四边形是平行四边形。 证明:设四边形ABCD的对角线AC,BD相交于点0且互相平分, 由图可见, AB=40+OB-OCDO-DO+OC-DC. 因此AB∥OC,且AB日DC, 故四边形ABCD是平行四边形。 例3:在平行六面体ABCD-ABCD中,设 AB=a,AD=b,AA=c, 试用a,b,c 表示向量AG,AC. 作业题:习题1.1:1,2,3,4,5

§1.3数乘向量 教学目的 掌握数量乘向量的定义、运算规律和在论证简单几何命题中的应用。 教学重点:掌握数量乘向量的定义、运算规律和在论证简单几何命题中的 应用。 教学难点:用向量的运算论证简单几何命题。 教学内容 1.定义实数九与a的乘积是一个向量,记为乙a, |a曰‖a|,当X>0时,元a与a同向 当入<0时,元a与a反向。 ia A ,a (2<0) 我们把这种运算叫做数量与向量的乘法,简称为数乘。 注:由数乘的定义可知 (i)九=0或a=0时,元a=0。 (ii)(-1)a=-a(既(-1)a为a的反向量) 证明:因为(-1)a=-1‖a=a|,且(-l)a与a反向(数乘定义),所以 由反向量的定义知(-1)a为a的反向量,即(-1)a=-d (iii)aaa°或a°= 2.运算规律 定理1.3.1数乘满足 1)1a=4 2)结合律: A(ua)=(Au)a

3)第一分配律:(1+0)石=a+ud 4)第二分配律:(石+b)=ā+b 以上a,b为任意向量,几,“为任意实数。 证明:1)因为1a与a同向且1a=1a=a,(数乘定义),所以1a=a, (两向量相等的定义)。 2)1°当a-0或0时,(ua)=0=(a成立。 2°当a≠0且u≠0时, 若>0,则(0)a与a同向,因乙,“同号,所以(@)与a同向,故(u)a 与(@)同向。 若u<0,则(u)a与a反向,因乙,“异号,所以2()与a反向,故()a 与2(a)同向。 总之,(awa与(u@同向。又因lw四d=h4同=24a=a 所以(n)a=(@)。 3)当a=0或九,4,几+“中至少有一个为零,等式显然成立。事实上, 1°当a=0时,(⑦+0)ā=0,2a+d-0,故(1+)a=ā+d。 20当2=0时,(⑦+)a=d=0+d=a+ud。 3°当=0时类似。 4°当元+=0时, a+1a=a+(-元)a=a+[-(a)]=00=a=(元+0)a。 以下只须证a≠0,≠0,几+“≠0时的情形。 i)若>0,则九,4,几+“同号,因此(+)ā与a+i要么都与a反 向,要么都与a同向,故(+0ā与后+ā同向,又因

(h+u)a=h+ua=(+u)a_a a+ua ha+ua ha+ua 所以 (+)a=a+ua。 ii)若<0,不妨设元>0,“<0,再分元+4>0和2+“<0两种情形, 下只证前一种情形,后一种情形证明类似。 设元>0,“<0,元+>0,(⑦+)ā+(-)a=[(2+0)+(-0)]a=a, 因此(2+)a=a-(-u)a =a+(-(-)ā) =a+(-1)(-0)a=2a+(-1)(-)ā=a+ā, 所以(+)a=a-(-)a=a+ua。 4)若元=0或ā,b之中有一个为0,等式显然成立。 因此只须对云≠0,b≠0且入≠0的情形进行证明。 i)若d,b共线,先证此时=mb,其中 同 ,a,b同向 m= a ,a,b反向 当a,6同向时,因rd>0,所以m6与i同向,故m5与ā同向。 当a,6反向时,因r1d<0,所以m6与5反向,故m6与a同向. 总之,mb与ā同向。 又因 网-啊-A-问 所以a=mb。于是