
4=月osa=,c0sa 式中0,=号为横装面上的正应力. 总应力P。是矢量,可将它沿截面的法向和切向分解为两个分量: 正应力。和剪应力t。 。它们为 Pa cosa=o cos2a ta=P.sin a=o cosasn a=sin 2a (c)这就是拉(压)杆斜截面上的正应力計算公式。其中α自杆轴转至 斜截面的外法线,以逆时针为正,顺时针为负。正应力及剪应力的符 号规则同前所述。使用公式时注意连同符号代入运算。 由式(c)可知: 1.o。和t。都是α的函数。即同一点处的应力随过该点的斜截面 的方向不同而改变。 2.当a=0°时,0。=0。,它是0。中的最大值,即杆内任一点处 的最大正应力发生在杆的横截面上。 3。当公=4伊时,,受,它是,中的最大值,即杆内任一点 处的最大剪应力发生在45“斜截面上,其值等于该点处最大正应力的 半。 4.当a=90°时,0。=0,t。=0,即在杆的纵向截面上无应力存 在。 通过以上分析,我们已经清楚地了解了拉(压)杆内任一点处各 个不同方向截面上的应力情况。 我们把通过一点的所有不同方向截面上应力情况的总和称为该点 处的应力状态。由式(©)可知,在所研究的拉(压)杆中,一点处的 应力状态由其横截面上的正应力。即可完全确定,这样的应力状态就 称为单向应力状态
cos cos = = = 0 A P A N p 式中 A P 0 = 为横截面上的正应力。 总应力 p 是矢量,可将它沿截面的法向和切向分解为两个分量: 正应力 和剪应力 。它们为 = = = = = sin 2 2 sin cos sin cos cos 0 0 2 0 p p (c)这就是拉(压)杆斜截面上的正应力計算公式。其中 自杆轴转至 斜截面的外法线,以逆时针为正,顺时针为负。正应力及剪应力的符 号规则同前所述。使用公式时注意连同符号代入运算。 由式(c)可知: 1. 和 都是 的函数。即同一点处的应力随过该点的斜截面 的方向不同而改变。 2.当 = 0 0 时, = 0 ,它是 中的最大值,即杆内任一点处 的最大正应力发生在杆的横截面上。 3.当 = 450 时, = 2 0 ,它是 中的最大值,即杆内任一点 处的最大剪应力发生在 450 斜截面上,其值等于该点处最大正应力的一 半。 4.当 = 900 时, = 0, = 0,即在杆的纵向截面上无应力存 在。 通过以上分析,我们已经清楚地了解了拉(压)杆内任一点处各 个不同方向截面上的应力情况。 我们把通过一点的所有不同方向截面上应力情况的总和称为该点 处的应力状态。由式(c)可知,在所研究的拉(压)杆中,一点处的 应力状态由其横截面上的正应力 0 即可完全确定,这样的应力状态就 称为单向应力状态
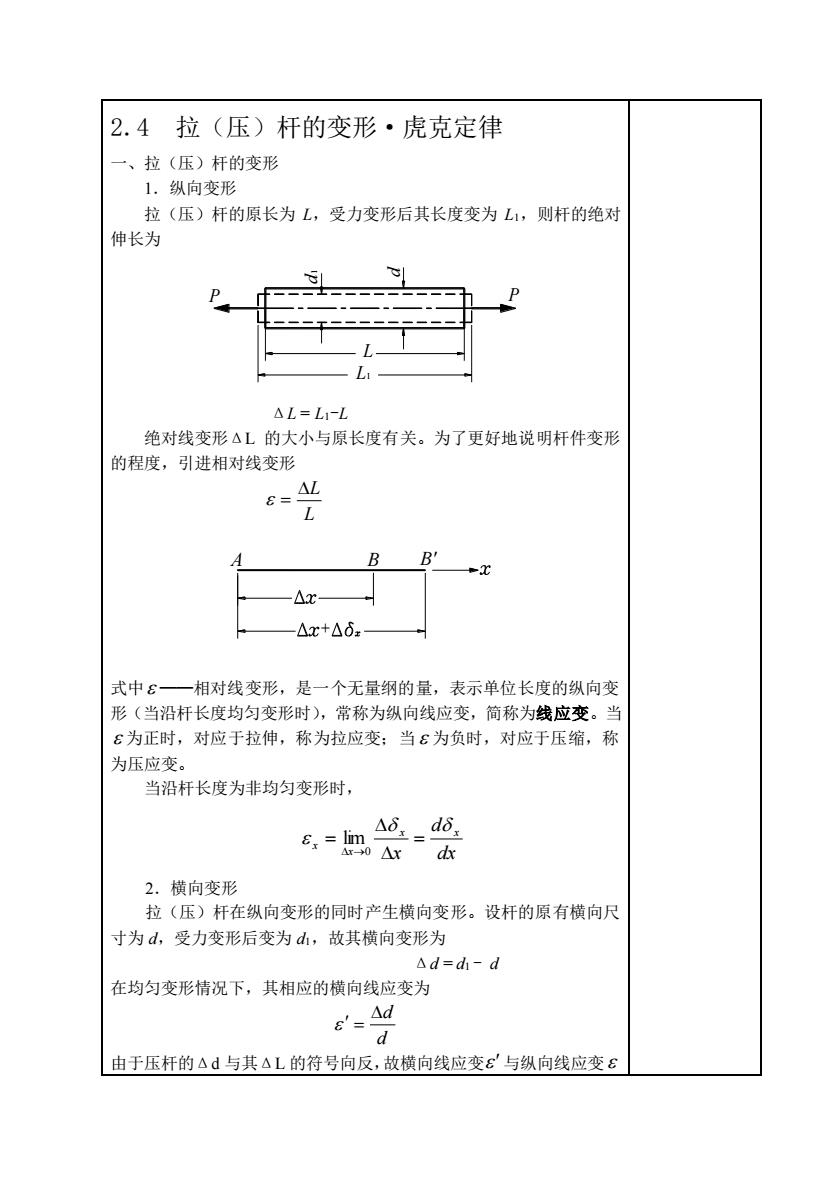
2.4拉(压)杆的变形·虎克定律 “、拉(压)杆的变形 1.纵向变形 拉(压)杆的原长为L,受力变形后其长度变为L,则杆的绝对 伸长为 △L=L1-L 绝对线变形△L的大小与原长度有关。为了更好地说明杆件变形 的程度,引进相对线变形 E=AL B B -x -△x -△x+△62 式中£一相对线变形,是一个无量纲的量,表示单位长度的纵向变 形(当沿杆长度均匀变形时),常称为纵向线应变,简称为线应变。当 6为正时,对应于拉伸,称为拉应变:当£为负时,对应于压缩,称 为压应变。 当沿杆长度为非均匀变形时, 6,=mA 2.横向变形 拉(压)杆在纵向变形的同时产生横向变形。设杆的原有横向尺 寸为d,受力变形后变为d山,故其横向变形为 △d=-d 在均匀变形情况下,其相应的横向线应变为 6'=Ad d 由于压杆的△d与其△L的符号向反,故横向线应变£'与纵向线应变E
2.4 拉(压)杆的变形·虎克定律 一、拉(压)杆的变形 1.纵向变形 拉(压)杆的原长为 L,受力变形后其长度变为 L1,则杆的绝对 伸长为 P P L1 L d1 d ΔL = L1-L 绝对线变形ΔL 的大小与原长度有关。为了更好地说明杆件变形 的程度,引进相对线变形 L L = + A B B' 式中 ──相对线变形,是一个无量纲的量,表示单位长度的纵向变 形(当沿杆长度均匀变形时),常称为纵向线应变,简称为线应变。当 为正时,对应于拉伸,称为拉应变;当 为负时,对应于压缩,称 为压应变。 当沿杆长度为非均匀变形时, dx d x x x x x = = →0 lim 2.横向变形 拉(压)杆在纵向变形的同时产生横向变形。设杆的原有横向尺 寸为 d,受力变形后变为 d1,故其横向变形为 Δd = d1 - d 在均匀变形情况下,其相应的横向线应变为 d d = 由于压杆的Δd 与其ΔL 的符号向反,故横向线应变 与纵向线应变

的正负号相反。 二、虎克定律 对工程中常用的材料,经大量的实验表明,当杆内的应力不超过 材料的某一极限(比例极限)时,力与变形之间存在以下关系 AL PL A 引进比例常数E,则 PL NL AL-EAEA ()式中的比例常数E称为弹性模量,它表示材料在拉伸或压缩时抵 抗弹性变形的能力,其量纲为[力]/[长度],单位为帕。E的数值随材 料而异,是通过实验测定的。 EA称为杆的抗拉(抗压)刚度,对于长度相等且受力相同的拉(压 杆,其抗拉(压)刚度越大,则杆件的变形越小。 以。=N/A和s=△LL代入(a)式,则得 (b)式()与式(b)是虎克定律的两种不同的表达方式。前者是为 杆的,只适用于受轴向外力的杆件。后者是针对杆中一点的,而拉(压) 杆中任一点的应力状态是单向应力状态,所以,凡是单向应力状态 式(b)均适用。 实验结果还表明,当拉(压)杆内的应力不超过材料的比例极限 时, 周 或改写为 E'=-g 式中负号表示'与ε的正负号恒相反。称为横向变形系数或泊松比, 是一个无量纲的量,其数值随材料而异,也是通过实验测定的。 2.5拉(压)杆内的应变能 一、应变能 弹性体在受力后要发生变形,同时弹性体内将积蓄能量。这种因 弹性变形而积蓄在弹性体内的能量,称为“弹性应变能”或简称为“应 变能”。略去其它微小的能量损耗不计,可以证明应变能在数值上等于 外力对弹性体所作的功。 U=W
的正负号相反。 二、虎克定律 对工程中常用的材料,经大量的实验表明,当杆内的应力不超过 材料的某一极限(比例极限)时,力与变形之间存在以下关系: A PL L 引 进 比 例 常 数 E , 则 EA NL EA PL L = = (a)式中的比例常数 E 称为弹性模量,它表示材料在拉伸或压缩时抵 抗弹性变形的能力,其量纲为[力]/[长度] 2,单位为帕。E 的数值随材 料而异,是通过实验测定的。 EA 称为杆的抗拉(抗压)刚度,对于长度相等且受力相同的拉(压) 杆,其抗拉(压)刚度越大,则杆件的变形越小。 以 = N A 和 = L L 代入(a)式,则得 E = (b)式(a)与式(b)是虎克定律的两种不同的表达方式。前者是对 杆的,只适用于受轴向外力的杆件。后者是针对杆中一点的,而拉(压) 杆中任一点的应力状态是单向应力状态,所以,凡是单向应力状态, 式(b)均适用。 实验结果还表明,当拉(压)杆内的应力不超过材料的比例极限 时, = 或改写为 = − 式中负号表示 与 的正负号恒相反。 称为横向变形系数或泊松比, 是一个无量纲的量,其数值随材料而异,也是通过实验测定的。 2.5 拉(压)杆内的应变能 一、应变能 弹性体在受力后要发生变形,同时弹性体内将积蓄能量。这种因 弹性变形而积蓄在弹性体内的能量,称为“弹性应变能”或简称为“应 变能”。略去其它微小的能量损耗不计,可以证明应变能在数值上等于 外力对弹性体所作的功。 U = W
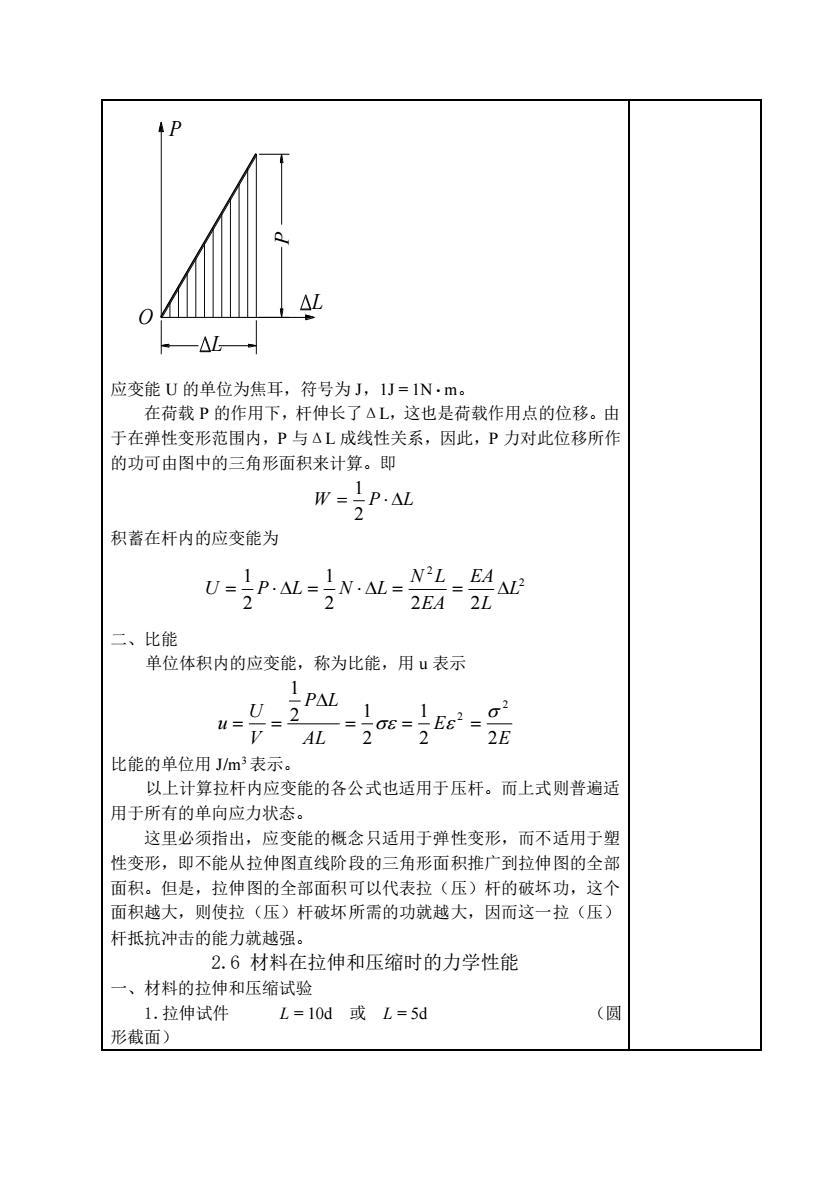
AL -△L 应变能U的单位为焦耳,符号为J,1J=1Nm。 在荷载P的作用下,杆伸长了△L,这也是荷载作用点的位移。由 于在弹性变形范围内,P与△L成线性关系,因此,P力对此位移所作 的功可由图中的三角形面积来计算。即 W-TP-AL 积蓄在杆内的应变能为 U-TP-AL-IN.AL-L-N 二、比 单位体积内的应变能,称为比能,用u表示 PAL - 1 u= 2E 比能的单位用Jm表示。 以上计算拉杆内应变能的各公式也适用于压杆。而上式则普遍适 用于所有的单向应力状态。 这里必须指出,应变能的概念只适用于弹性变形,而不适用于塑 性变形,即不能从拉伸图直线阶段的三角形面积推广到拉伸图的全部 面积。但是,拉伸图的全部面积可以代表拉(压)杆的破坏功,这个 面积越大,则使拉(压)杆破坏所需的功就越大,因而这一拉(压) 杆抵抗冲击的能力就越强。 2.6材料在拉伸和压缩时的力学性能 一、材料的拉伸和压缩试验 1.拉伸试件 L=10d或L=5d (圆 形截面)
O P L L P 应变能 U 的单位为焦耳,符号为 J,1J = 1N·m。 在荷载 P 的作用下,杆伸长了ΔL,这也是荷载作用点的位移。由 于在弹性变形范围内,P 与ΔL 成线性关系,因此,P 力对此位移所作 的功可由图中的三角形面积来计算。即 W = P L 2 1 积蓄在杆内的应变能为 2 2 2 2 2 1 2 1 L L EA EA N L U = P L = N L = = 二、比能 单位体积内的应变能,称为比能,用 u 表示 E E AL P L V U u 2 2 1 2 2 1 1 2 2 = = = = = 比能的单位用 J/m3 表示。 以上计算拉杆内应变能的各公式也适用于压杆。而上式则普遍适 用于所有的单向应力状态。 这里必须指出,应变能的概念只适用于弹性变形,而不适用于塑 性变形,即不能从拉伸图直线阶段的三角形面积推广到拉伸图的全部 面积。但是,拉伸图的全部面积可以代表拉(压)杆的破坏功,这个 面积越大,则使拉(压)杆破坏所需的功就越大,因而这一拉(压) 杆抵抗冲击的能力就越强。 2.6 材料在拉伸和压缩时的力学性能 一、材料的拉伸和压缩试验 1.拉伸试件 L = 10d 或 L = 5d (圆 形截面)
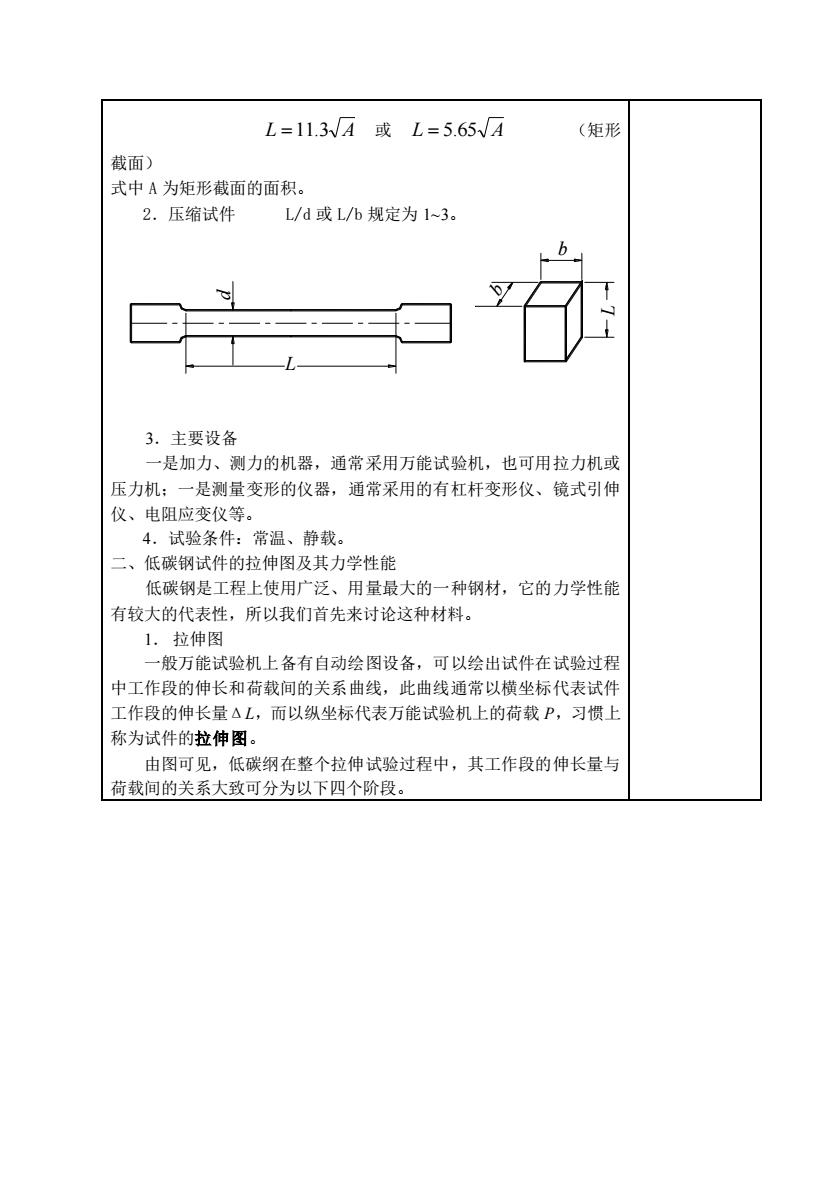
L=11.3A或L=5.65√A (矩形 截面) 式中A为矩形截面的面积。 2.压缩试件 L/d或L/b规定为1~3. 3.主要设备 一是加力、测力的机器,通常采用万能试验机,也可用拉力机或 压力机:一是测量变形的仪器,通常采用的有杠杆变形仪、镜式引伸 仪、电阻应变仪等。 4.试验条件:常温、静载 二、低碳钢试件的拉伸图及其力学性能 低碳钢是工程上使用广泛、用量最大的一种钢材,它的力学性能 有较大的代表性,所以我们首先来讨论这种材料。 1.拉伸图 一般万能试验机上备有自动绘图设备,可以绘出试件在试验过程 中工作段的伸长和荷载间的关系曲线,此曲线通常以横坐标代表试 工作段的伸长量△L,而以纵坐标代表万能试验机上的荷载P,习惯上 称为试件的拉伸图。 由图可见,低碳纲在整个拉伸试验过程中,其工作段的伸长量与 荷载间的关系大致可分为以下四个阶段
L =11.3 A 或 L = 5.65 A (矩形 截面) 式中 A 为矩形截面的面积。 2.压缩试件 L/d 或 L/b 规定为 1~3。 d L L b b 3.主要设备 一是加力、测力的机器,通常采用万能试验机,也可用拉力机或 压力机;一是测量变形的仪器,通常采用的有杠杆变形仪、镜式引伸 仪、电阻应变仪等。 4.试验条件:常温、静载。 二、低碳钢试件的拉伸图及其力学性能 低碳钢是工程上使用广泛、用量最大的一种钢材,它的力学性能 有较大的代表性,所以我们首先来讨论这种材料。 1. 拉伸图 一般万能试验机上备有自动绘图设备,可以绘出试件在试验过程 中工作段的伸长和荷载间的关系曲线,此曲线通常以横坐标代表试件 工作段的伸长量ΔL,而以纵坐标代表万能试验机上的荷载 P,习惯上 称为试件的拉伸图。 由图可见,低碳纲在整个拉伸试验过程中,其工作段的伸长量与 荷载间的关系大致可分为以下四个阶段