
Tutorial 5:General Random Variables 1 MENG Yitong ytmeng@cse.cuhk.edu.hk 27,February,2016 1
Tutorial 5: General Random Variables 1 MENG Yitong ytmeng@cse.cuhk.edu.hk 27, February, 2016 1

Outline Continuous random variables,PDFs,CDFs Uniform distributions Exponential distributions Normal distributions Laplace distributions
Outline • Continuous random variables, PDFs, CDFs • Uniform distributions • Exponential distributions • Normal distributions • Laplace distributions 2

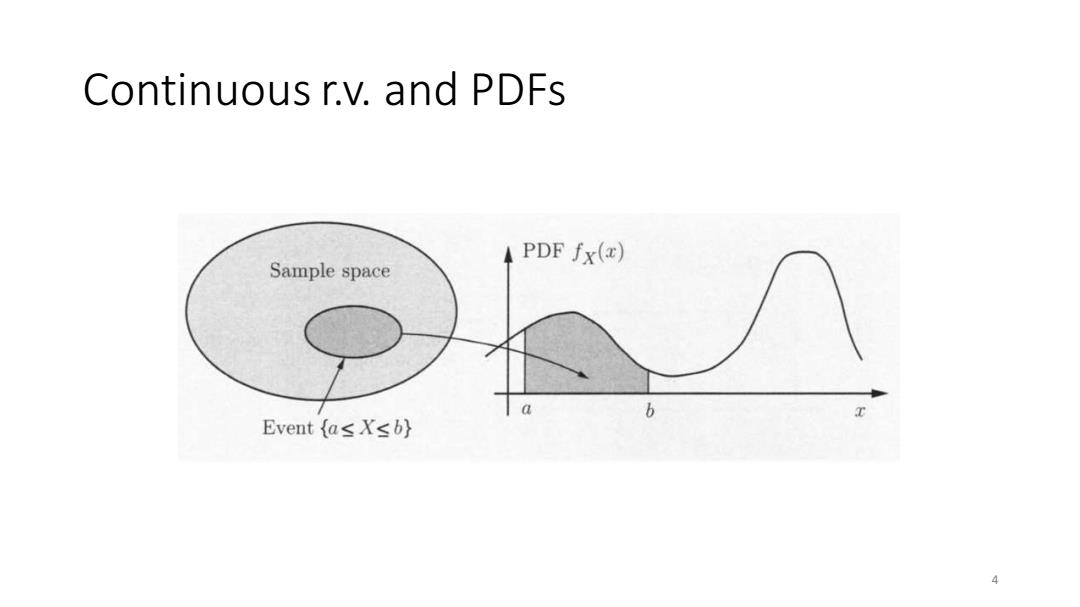
Continuous r.v.and PDFs A random variable X is called continuous if there is a functionfx>0, called the probability density function of X,or PDF,s.t. P(X E B)=fx(x)dx for every subset B≤R. In particular,when B [a,b], P(a≤X≤b)=fx(x)dx is the area under the graph of PDF
Continuous r.v. and PDFs • A random variable 𝑋 is called continuous if there is a function 𝑓𝑋 ≥ 0, called the probability density function of 𝑋, or PDF, s.t. 𝑃(𝑋 ∈ 𝐵) = න 𝐵 𝑓𝑋 𝑥 𝑑𝑥 for every subset 𝐵 ⊆ ℝ. • In particular, when 𝐵 = [𝑎, 𝑏], 𝑃(𝑎 ≤ 𝑋 ≤ 𝑏) = න 𝑎 𝑏 𝑓𝑋 𝑥 𝑑𝑥 is the area under the graph of PDF. 3
Continuous r.v.and PDFs PDF fx(t) Sample space b Event fas Xsb} 4
Continuous r.v. and PDFs 4

Cumulative Distribution Function The cumulative distribution function,or CDF,of a random variablex is Fx(x)=P(X≤x) ∑ksx Px(x),( discrete fx(x)dx,continuous The CDF Fx(x)"accumulates"probability "up to"the value x
Cumulative Distribution Function • The cumulative distribution function, or CDF, of a random variable 𝑋 is 𝐹𝑋 𝑥 = 𝑃 𝑋 ≤ 𝑥 = ൝ σ𝑘≤𝑥 𝑝𝑋 𝑥 , discrete ∞− 𝑥 𝑓𝑋 𝑥 𝑑𝑥 , continuous • The CDF 𝐹𝑋 𝑥 “accumulates” probability “up to” the value 𝑥