
Tutorial 2:Sample Space and Probability 2 Baoxiang WANG bxwang@cse Spring 2017
Tutorial 2: Sample Space and Probability 2 Baoxiang WANG bxwang@cse Spring 2017

Probability models A probability model is an assignment of probabilities to every element of the sample space. Probabilities are nonnegative and add up to one. Examples S=HH,HT,TH,TT /44/4/4 107 models a pair of coins with equally likely outcomes
Probability models A probability model is an assignment of probabilities to every element of the sample space. Probabilities are nonnegative and add up to one. S = { HH, HT, TH, TT } ¼ ¼ ¼ ¼ Examples models a pair of coins with equally likely outcomes

Elements of a Probabilistic Model Event:a subset of sample space. -A is a set of possible outcomes -Example.A ={HH,T'T},the event that the two coins give the same side. The probability law assigns our knowledge or belief to an event Aa number P(A)0. It specifies the likelihood of any outcome
Elements of a Probabilistic Model • Event: a subset of sample space. – 𝐴 ⊆ Ω is a set of possible outcomes – Example. 𝐴 = 𝐻𝐻, 𝑇𝑇 , the event that the two coins give the same side. • The probability law assigns our knowledge or belief to an event 𝐴 a number 𝑃 𝐴 ≥ 0. – It specifies the likelihood of any outcome

Probability Axioms 1.(Won-negativity)P(A)≥0,for every event A. 2.(Additivity)For any two disjoint events A and B,P(AUB)=P(A)+P(B) In general,if A1,A2,..are disjoint events, then P(A1UA2U…)=P(A1)+P(A2)+… 3.(Normalization)P()=1
Probability Axioms 1. (Non-negativity) 𝑃(𝐴) ≥ 0, for every event 𝐴. 2. (Additivity) For any two disjoint events 𝐴 and 𝐵, 𝑃 𝐴 ∪ 𝐵 = 𝑃 𝐴 + 𝑃 𝐵 In general, if 𝐴1, 𝐴2, … are disjoint events, then 𝑃 𝐴1 ∪ 𝐴2 ∪ ⋯ = 𝑃 𝐴1 + 𝑃 𝐴2 + ⋯ 3. (Normalization) 𝑃(Ω) = 1
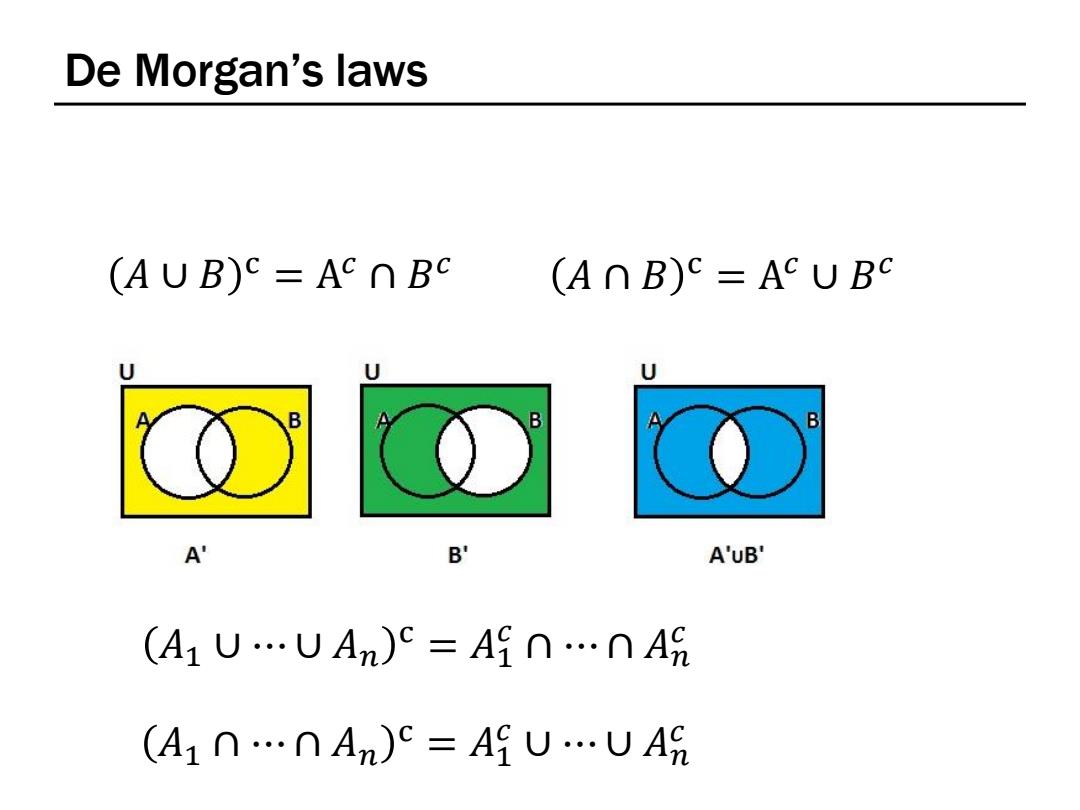
De Morgan's laws (AUB)c=AC∩Bc (AnB)C=ACUB U U B B B A' B' A'uB' (A1UUAn)C=An…nA8 (A1n…nAn)c=AUUA9
De Morgan’s laws 𝐴 ∪ 𝐵 c = A 𝑐 ∩ 𝐵 𝑐 𝐴 ∩ 𝐵 c = A 𝑐 ∪ 𝐵 𝑐 𝐴1 ∪ ⋯ ∪ 𝐴𝑛 c = 𝐴1 𝑐 ∩ ⋯ ∩ 𝐴𝑛 𝑐 𝐴1 ∩ ⋯ ∩ 𝐴𝑛 c = 𝐴1 𝑐 ∪ ⋯ ∪ 𝐴𝑛 𝑐