
ENGG2430 ProbabStatistics forners Chapter 3:General Random Variables Instructor: Shengyu Zhang
Instructor: Shengyu Zhang

Content Continuous random variables and PDEs Cumulative Distribution Functions Normal Random Variables Joint PDFs of Multiple Random Variables Conditioning The Continuous Bayes'Rule
Content ◼ Continuous Random Variables and PDFs ◼ Cumulative Distribution Functions ◼ Normal Random Variables ◼ Joint PDFs of Multiple Random Variables ◼ Conditioning ◼ The Continuous Bayes’ Rule

Continuous random variables We've learned discrete random variables. which can be used for dice rolling,coin flipping,etc. Random variables with a continuous range of possible values are quite common. velocity of a vehicle traveling along the highway Continuous random variables are useful: finer-grained than discrete random variables able to exploit powerful tools from calculus
Continuous Random Variables ◼ We’ve learned discrete random variables, which can be used for dice rolling, coin flipping, etc. ◼ Random variables with a continuous range of possible values are quite common. ❑ velocity of a vehicle traveling along the highway ◼ Continuous random variables are useful: ❑ finer-grained than discrete random variables ❑ able to exploit powerful tools from calculus

Continuous r.v.and PDFs A random variable X is called continuous if there is a functionf =0,called the probability density function of X,or PDF,s.t. P(XEB)=fx(x)dx for every subset B R. We assume the integral is well-defined Compared to discrete case:replace summation by integral
Continuous r.v. and PDFs ◼ A random variable 𝑋 is called continuous if there is a function 𝑓𝑋 ≥ 0, called the probability density function of 𝑋, or PDF, s.t. 𝑃 𝑋 ∈ 𝐵 = න 𝐵 𝑓𝑋 𝑥 𝑑𝑥 for every subset 𝐵 ⊆ ℝ. ❑ We assume the integral is well-defined. ◼ Compared to discrete case: replace summation by integral
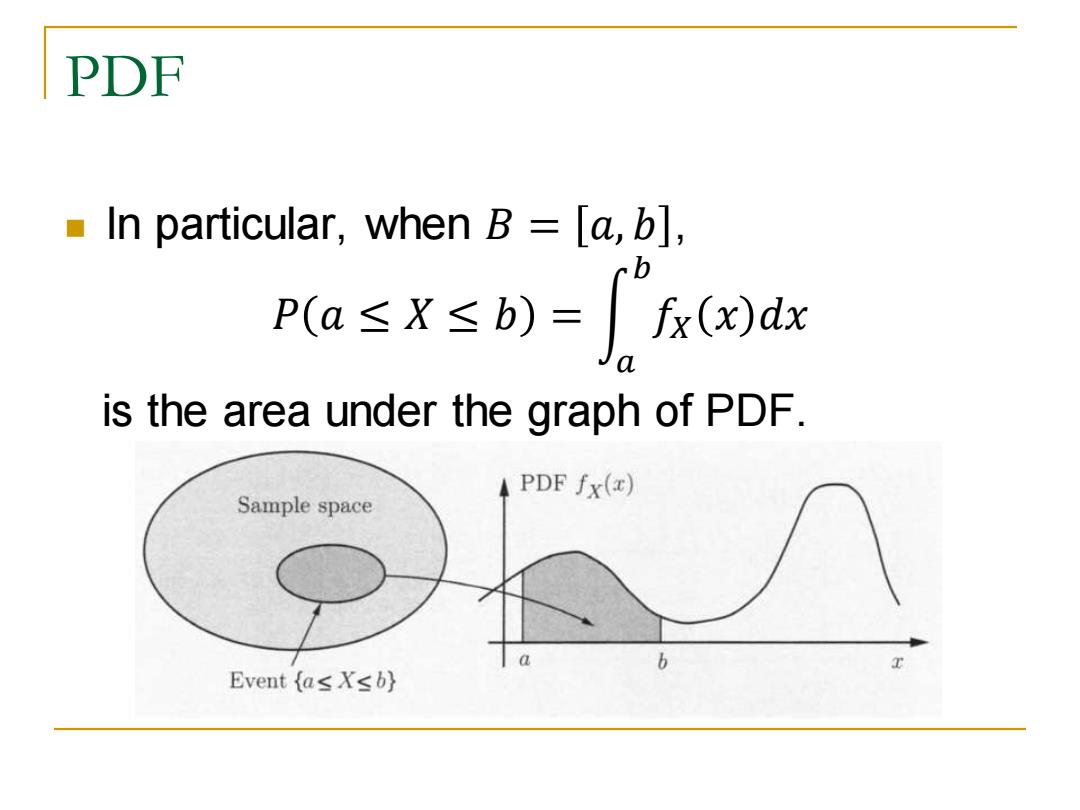
PDF In particular,when B [a,b], p(a≤x≤b)=fx()dx is the area under the graph of PDF. PDF fx(x) Sample space b Event {as Xsb}
PDF ◼ In particular, when 𝐵 = 𝑎, 𝑏 , 𝑃 𝑎 ≤ 𝑋 ≤ 𝑏 = න 𝑎 𝑏 𝑓𝑋 𝑥 𝑑𝑥 is the area under the graph of PDF