
例6-1100W普通白炽灯辐射光通量为1250lm,假设光源向 四周辐射的光通量是均匀的,求光源某方向上的光强。 解:根据题意,光源向四周辐射的光通量是均匀的,因 此在任一方向上的光强也是相等的,故可以光源为球心, 作一半径为的球面,球面积4π2,其立体角为 4m2 =4πSr 1250 故各方向光强为 cd=99.5cd 4π
例6-1 100W普通白炽灯辐射光通量为1250lm,假设光源向 四周辐射的光通量是均匀的,求光源某方向上的光强。 解: 根据题意,光源向四周辐射的光通量是均匀的,因 此在任一方向上的光强也是相等的,故可以光源为球心, 作一半径为r的球面,球面积4πr 2,其立体角为 故各方向光强为 4 4 2 2 2 = = = r r r A Sr cd=99.5cd 4 1250 = I =
三.照度(illuminance) (1)照度概念 光通量和光强通常用来表征光源发射的光通量的强弱,而 照度用来表示被照面单位上面积上接受的光通量的强弱, 用符号E表示,单位勒克斯(x)。 例如图6-4,设被照面上有一点P,取该面上P周围的一足 够小的面元dA,若面元dA接受的光通量为dΦ,则P处的照 度为 dΦ dA (6-3) dΦ 图6-4照度
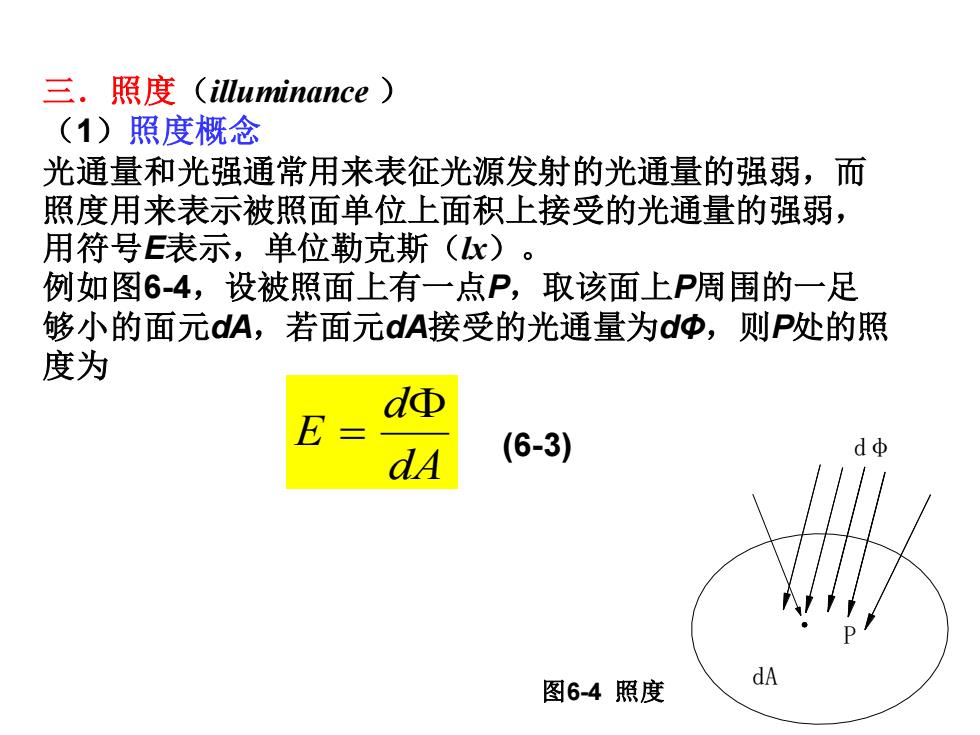
三.照度(illuminance ) (1)照度概念 光通量和光强通常用来表征光源发射的光通量的强弱,而 照度用来表示被照面单位上面积上接受的光通量的强弱, 用符号E表示,单位勒克斯(lx)。 例如图6-4,设被照面上有一点P,取该面上P周围的一足 够小的面元dA,若面元dA接受的光通量为dΦ,则P处的照 度为 (6-3) dA d E = dA P dφ 图6-4 照度

例题: 100W普通白炽灯辐射光通量为1250lm,假设光 源向四周辐射的光通量是均匀的,求灯下2m处的 照度值。 解:仍以点光源为球心作半径为2的球面,球面内侧接收 的光通量也是均匀的,故球面内侧的照度为 Φ Φ 1250 E- A 2 1x=24.91x 4 4π×22
例题: 100W普通白炽灯辐射光通量为1250lm,假设光 源向四周辐射的光通量是均匀的,求灯下2m处的 照度值。 2 2 4 2 1250 4 = = = A r E lx=24.9lx 解: 仍以点光源为球心作半径为2m 的球面,球面内侧接收 的光通量也是均匀的,故球面内侧的照度为

(2)光强与照度的关系 光源光强已知,它在任意方向某平面上形成的照度可由以下两 定律决定。 1)距离平方反比定律 当光源的直径小于它至被照面距离的1/5时,则可把该光源视 为点光源。 设有点光源位于半径为的球心,该光源向各方向均匀发光, 光强为I总光通量为Φ=4πI,则球的内表面各点的照度E为 Φ 4πd E= A 42
(2)光强与照度的关系 光源光强已知,它在任意方向某平面上形成的照度可由以下两 定律决定。 1)距离平方反比定律 当光源的直径小于它至被照面距离的1/5时,则可把该光源视 为点光源。 设有点光源位于半径为r的球心,该光源向各方向均匀发光, 光强为I总光通量为Φ=4πI,则球的内表面各点的照度E为 2 2 4 4 r I r I A E = = =

2)入射角余弦定律 如图6-5(b)所示,有一面积为A的平面A1,接受与平面成垂直方 向射来的光通量为中,则该平面的照度 Φ 今假定将此平面倾斜一个角度得面A,于是射入该平面的光通 量将变成Φcos0,因此该平面上的照度应为: Φcosθ Ee E,cos A 即任意平面的照度,与光线入射角(入射光的方向与平面法线 之间的夹角)的余弦成正比。这就是所谓入射角余弦定律
2)入射角余弦定律 如图6-5(b)所示,有一面积为A的平面A1,接受与平面成垂直方 向射来的光通量为Φ,则该平面的照度 A En = cos cos En A E = = 今假定将此平面倾斜一个角度θ得面A2,于是射入该平面的光通 量将变成Φcosθ,因此该平面上的照度应为: 即任意平面的照度,与光线入射角(入射光的方向与平面法线 之间的夹角)的余弦成正比。这就是所谓入射角余弦定律