
6.1傅里叶变换的模和相位表示 一般说来,傅里叶变换是复数值的,用它的模和相 位来表示。 连续时间傅里叶变换X)ω)的模一相表示: X(j@)=X(j@)eix() 离散时间傅里叶变换X()的模一相表示: X(e)=Y(e)
6.1 傅里叶变换的模和相位表示 一般说来,傅里叶变换是复数值的,用它的模和相 位来表示。 连续时间傅里叶变换X(jω)的模-相表示: 离散时间傅里叶变换X(ejω)的模-相表示: ( ) () () j X j Xj Xj e ω ω ω ∠ = ( ) () () j j jj X e Xe Xe e ω ω ω ∠ =

6.1傅里叶变换的模和相位表示 连续时间傅立叶变换(CFT)的模-相表示: 令信号x(t)的傅氏变换: x(t)←F→X(Ujw) Xjo-Xjol |X(jw)川---幅度频谱(Lagnitude Spectrum) ej2Xio)---相位频谱(Phase Spectrum) 第6章时域和频域特性 7
第6章时域和频域特性 7 6.1 傅里叶变换的模和相位表示 )( |)(|)( ω ωω jXj ejXjX ∠ = ( ) |)(| ( ) )( e Phase Spectrum jX Magnitude Spectrum jXj 相位频谱 幅度频谱 −−− −−− ∠ ω ω 连续时间傅立叶变换(CFT)的模-相表示: 信号 x(t)的傅氏变换 : jXtx ω)()( ←⎯→F

傅里叶变换式本身可以看做是信号x()的一种分解,即 把信号x()分解成不同频率的复指数信号之和: W-元xjoe4o 十∞ 由帕斯瓦尔定理,X(⊙)2可以看作是x()的能谱密 度;也就是X0w)Pdo/2π可以认为是信号x()中位于 频率由o到w十do之间这样一个无限小的频带内所占 有的能量。因此,模X0⊙)所描述的是一个信号的基 本频率含量,也即给出是组成x()的各复指数信号相对 振幅的信息
傅里叶变换式本身可以看做是信号 x ( t)的一种分解,即 把信号 x ( t)分解成不同频率的复指数信号之和: 由帕斯瓦尔定理,|X(j ω)| 2可以看作是x ( t)的能谱密 度;也就是 |X(j ω)| 2 d ω/2π可以认为是信号 x ( t)中位于 频率由ω到ω+ dω之间这样一个无限小的频带内所占 有的能量。因此, 模 |X(j ω)|所描述的是一个信号的基 本频率含量,也即给出是组成x ( t)的各复指数信号相对 振幅的信息 。 1 () ( ) 2 j t x t Xj e d ω ω ω π +∞ −∞ =

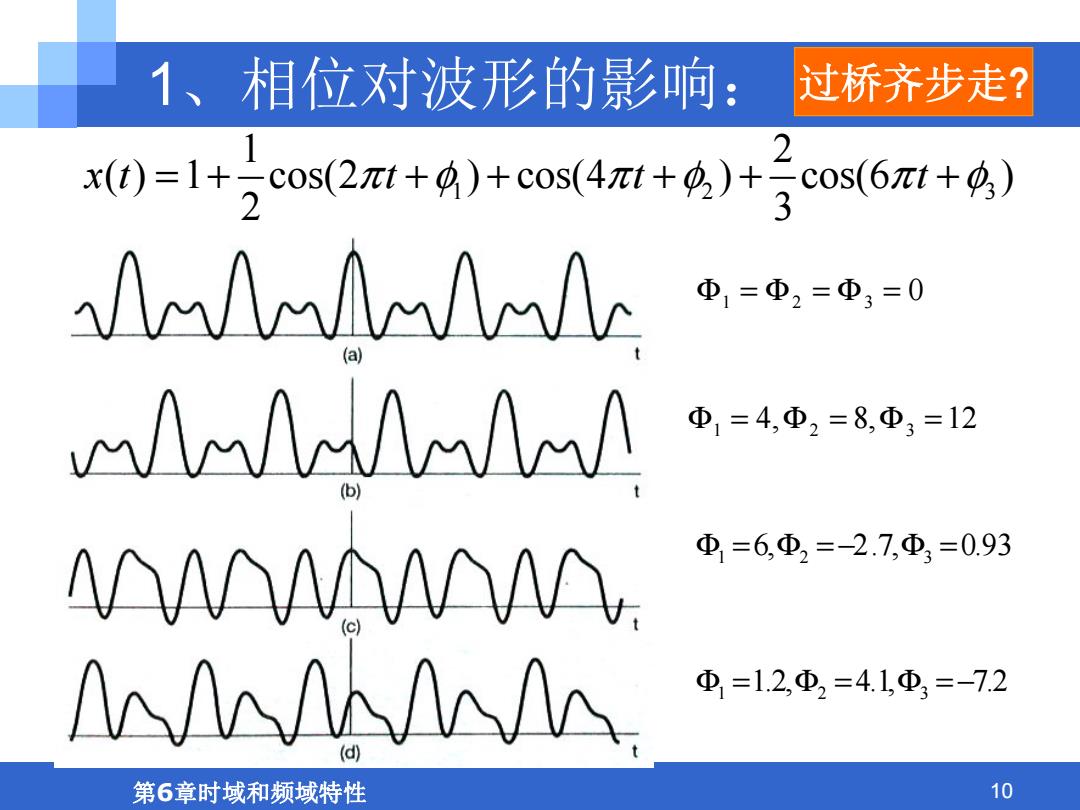
另一方面,相位角木X(ω)不影响各个频率分量的大 小,但是提供的是有关这些复指数信号的相对相位信 息。由卡X)⊙)所代表的相位关系对信号x()的本质属 性有显著的影响。尤其是,依赖于什么样的相位函 数,即使模函数保持不变,也能得出看上去很不相同 的信号。例如图3.3所示的例子,由于相对相位关系, 造成振幅叠加效应。 。作为相位影响的另一个例子,如下信号 x)=1+2cos(2mt+9)+cos(4t+9)+5cos(6t+4)
另一方面,相位角≮X(jω)不影响各个频率分量的大 小,但是提供的是有关这些复指数信号的相对相位信 息。由≮X( jω)所代表的相位关系对信号x(t)的本质属 性有显著的影响。尤其是,依赖于什么样的相位函 数,即使模函数保持不变,也能得出看上去很不相同 的信号。例如图3.3所示的例子,由于相对相位关系, 造成振幅叠加效应。 作为相位影响的另一个例子,如下信号 12 3 1 2 ( ) 1 cos(2 ) cos(4 ) cos(6 ) 2 3 xt t t t =+ + + + + + π φ π φ π φ
1、相位对波形的影响: 过桥齐步走? x0=1+)c0s(21+4)+c0s(4z1+4)+2c0s(671+4) △mmm ,Φ=Φ2=Φ=0 (a) WmML Φ1=4,Φ2=8,Φ3=12 AMA△AA Φ=6,Φ2=-2.7,Φ3=0.93 MMA Φ=1.2,Φ2=4.1,Φ3=-7.2 第6章时域和频域特性 10
第6章时域和频域特性 10 1、相位对波形的影响: 12 3 1 2 ( ) 1 cos(2 ) cos(4 ) cos(6 ) 2 3 xt t t t =+ + + + + + π φ π φ π φ 321 =Φ=Φ=Φ 0 1 2 3 =Φ=Φ=Φ 12,8,4 1 2 3 =Φ−=Φ=Φ 93.0,7.2,6 1 2 3 −=Φ=Φ=Φ 2.7,1.4,2.1 过桥齐步走?