
导数与微分 例2:求曲线y=lnx在x=e处的切线与法线方程。 解: y-(ny- 1、求导函数 2、求导数值=斜率 当x=e时,y=lne=1 3、求点的坐标 切线方程:y1cx-e) 写点斜式方程 法线方程: y-1=-e(x-e)
例2:求曲线𝒚 = 𝒍𝒏𝒙在𝒙 = 𝒆处的切线与法线方程。 解: 𝒚′ = (𝒍𝒏𝒙)′ = 𝟏 𝒙 切线方程: 法线方程: 𝒚 − 𝟏 = −𝒆(𝒙 − 𝒆) 当𝒙 = 𝒆时,𝒚 = 𝒍𝒏𝒆 = 𝟏 1、求导函数 2、求导数值=斜率 4、写点斜式方程 3、求点的坐标 𝒌 = ቤ 𝟏 𝒙 𝒙=𝒆 = 𝟏 𝒆 𝒚 − 𝟏 = 𝟏 𝒆 (𝒙 − 𝒆)
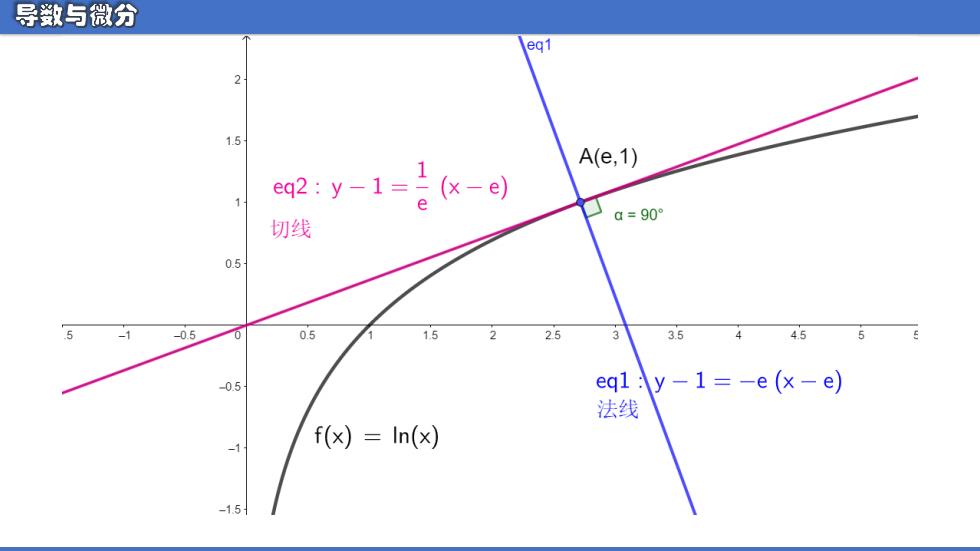
导数与微分 eq1 2 1.5 1 A(e,1) eq2:y-1=(x-e) a=90 切线 0.5 -0.5 0.5 2.5 3.5 0.5 eq1:y-1=-e(x-e) 法线 f(x)=In(x) -15