
3.电感元件储能 根据基尔霍夫定律可得 u=-e=L di dt 将上式两边同乘上i,并积分,则得 idr-可idi-L 磁场能 W-ILP 2 即电感将电能转换为磁场能储存在线圈中, 当电流增大时,磁场能增大,电感元件从电源取用 电能;当电流减小时,磁场能减小,电感元件向 电源放还能量。 ©中间对装天举 672 章目录上一页下一页返回退出
6/72 章目录 上一页 下一页 返回 退出 3. 电感元件储能 2 2 1 W = Li t i u eL L d d 根据基尔霍夫定律可得 = − = 将上式两边同乘上 i ,并积分,则得 2 0 0 2 1 ui dt Li di Li t i = = 即电感将电能转换为磁场能储存在线圈中, 当电流增大时, 磁场能增大, 电感元件从电源取用 电能;当电流减小时,磁场能减小,电感元件向 电源放还能量。 磁场能

3.1.3电容元件 描述电容两端加电源后,其两个极板 上分别聚集起等量异号的电荷,在介质 中建立起电场,并储存电场能量的性质。 电容 C= F) 电容元件 W 当电容电压变化时,在电路中产生电流 i=c du dt 将上式两边同乘上W,并积分,则得: id-cudn-Cu 雪中间对基天华 772 章目录上一页下一页返回退出
7/72 章目录 上一页 下一页 返回 退出 3.1.3 电容元件 描述电容两端加电源后,其两个极板 上分别聚集起等量异号的电荷,在介质 中建立起电场, 并储存电场能量的性质。 电容 u q C = (F ) t u i C d d = 当电容电压u变化时,在电路中产生电流 将上式两边同乘上 u,并积分,则得: 2 0 0 2 1 ui dt Cudu Cu t u = = u i C + _ 电容元件 u i C + _ 电容元件

电容元件储能 电场能 w=Icu 即电容将电能转换为电场能储存在电容中,当电压 增大时,电场能增大,电容元件从电源取用电能;当 电压减小时,电场能减小,电容元件向电源放还能 量。 本节所讲的均为线性元件,即R、L、C都是常数。 ©中间对装天举 8/72 章目录上一页下一页返回退出
8/72 章目录 上一页 下一页 返回 退出 即电容将电能转换为电场能储存在电容中,当电压 增大时, 电场能增大, 电容元件从电源取用电能;当 电压减小时,电场能减小,电容元件向电源放还能 量。 2 2 1 W = Cu 电场能 电容元件储能 本节所讲的均为线性元件,即R、L、C都是常数
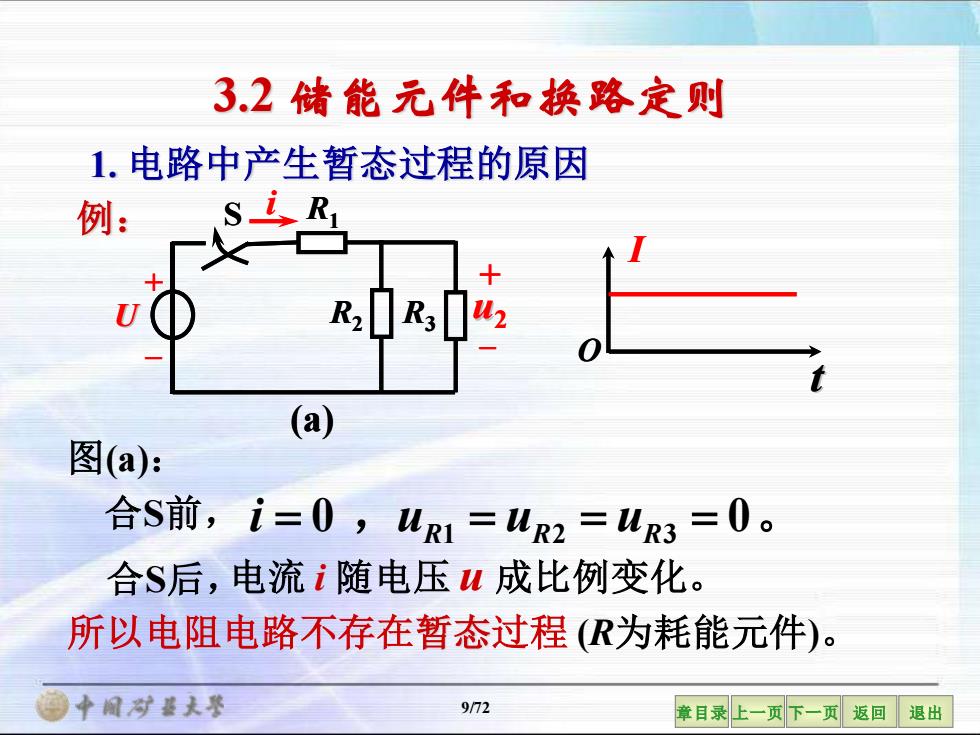
3.2储能元件和换路定则 1.电路中产生暂态过程的原因 例: (a) 图(a): 合S前,i=0,lR1=4R2=4R3=0。 合S后,电流i随电压u成比例变化。 所以电阻电路不存在暂态过程(R为耗能元件)。 湾中帽对装天$ 972 章目录上一页下一页返回退出
9/72 章目录 上一页 下一页 返回 退出 3.2 储能元件和换路定则 1. 电路中产生暂态过程的原因 合S后,电流 i 随电压 u 成比例变化。 所以电阻电路不存在暂态过程 (R为耗能元件)。 图(a): 合S前, i = 0 ,uR1 = uR2 = uR3 = 0。 例: t I O (a) S + _ U R2 R3 u2 + _ R1 i (a) S + _ U R2 R3 u2 + _ R1 i
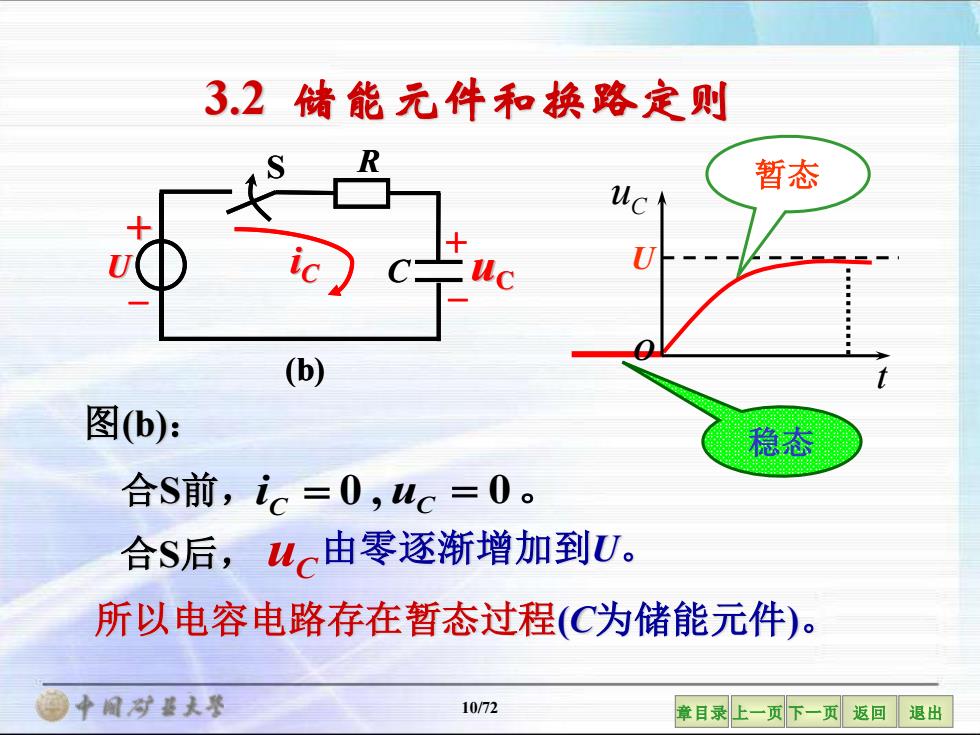
3.2储能元件和换路定则 暂态 (b) 图b): 稳态 合S前,ic=0,uc=0。 合S后,uc由零逐渐增加到U。 所以电容电路存在暂态过程(C为储能元件)。 酒中间对整大琴 10/72 章目录上一页下一页返回退出
10/72 章目录 上一页 下一页 返回 退出 3.2 储能元件和换路定则 图(b): 合S后, uC 由零逐渐增加到U。 所以电容电路存在暂态过程(C为储能元件)。 = 0 , C 合S前, i uC = 0。 U 暂态 稳态 O t C u uC + – iC C (b) U + – S R uC + – iC C (b) U + – S R