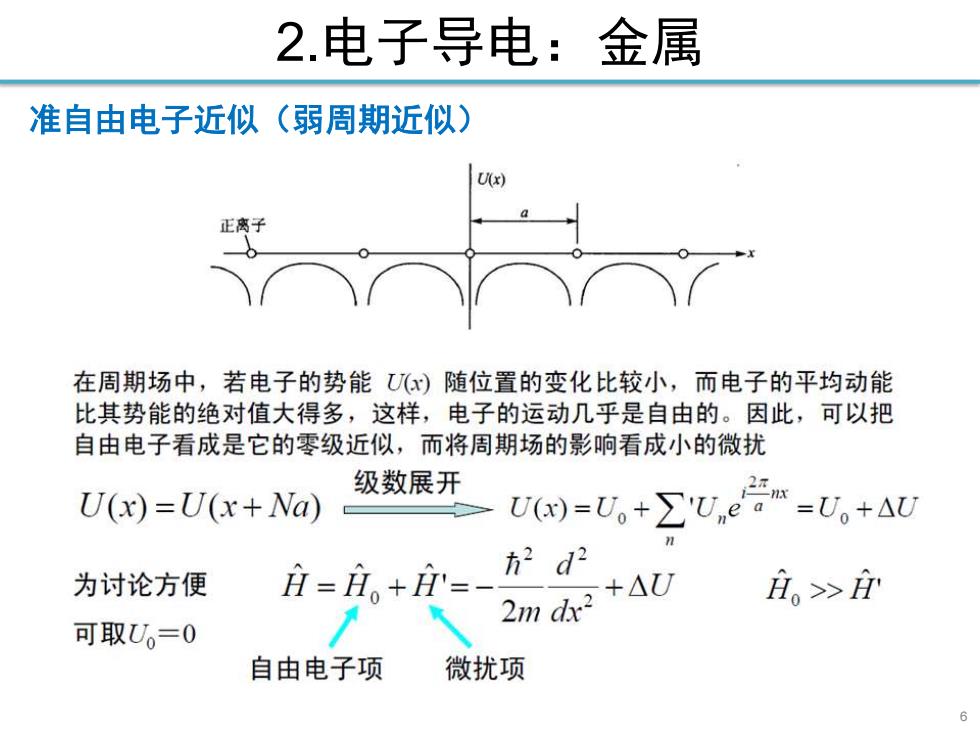
2.电子导电:金属 准自由电子近似(弱周期近似) U(x) 正离 在周期场中,若电子的势能(随位置的变化比较小,而电子的平均动能 比其势能的绝对值大得多,这样,电子的运动几乎是自由的。因此,可以把 自由电子看成是它的零级近似,而将周期场的影响看成小的微扰 级数展开 27 U(x)=U(x+Na) U(a)=U。+∑'Une=U。+AU 户=。+= 方2d2 为讨论方便 2m d?+AU 庄。>0 可取U。=0 自由电子项 微扰项 6
6 2.电子导电:金属 准自由电子近似(弱周期近似)
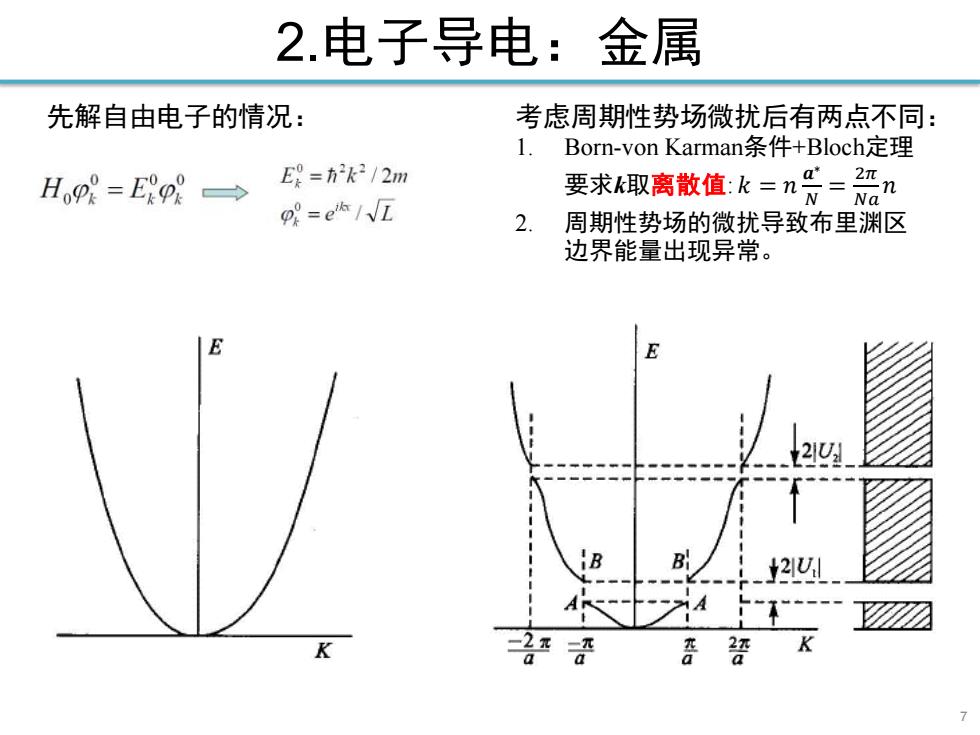
2.电子导电:金属 先解自由电子的情况: 考虑周期性势场微扰后有两点不同: 1. Borm-von Karman条件+Bloch.定理 Hp=ERp8→ E9=方k2/2m p=eh/√D 要求取离散值:k三n号=名 2.周期性势场的微扰导致布里渊区 边界能量出现异常。 E B B 2红
7 2.电子导电:金属 先解自由电子的情况: 考虑周期性势场微扰后有两点不同: 1. Born-von Karman条件+Bloch定理 要求k取离散值: 𝑘 = 𝑛 𝒂 ∗ 𝑁 = 2𝜋 𝑁𝑎 𝑛 2. 周期性势场的微扰导致布里渊区 边界能量出现异常
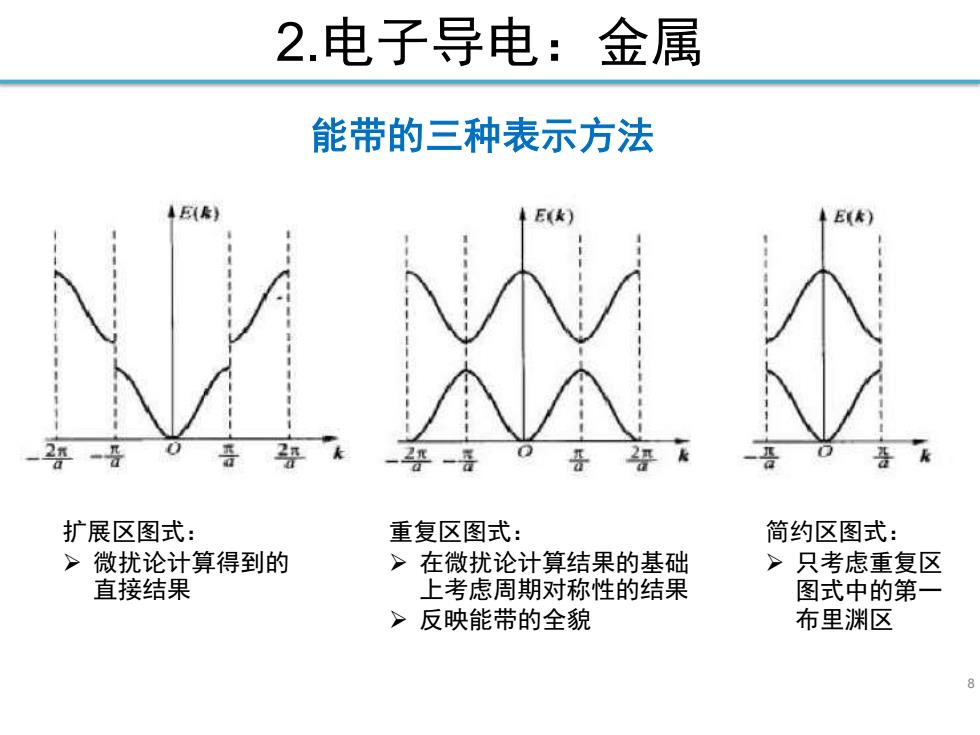
2.电子导电:金属 能带的三种表示方法 E(A) E 4Ek) 2- 2g- 扩展区图式: 重复区图式: 简约区图式: 微扰论计算得到的 > 在微扰论计算结果的基础 >只考虑重复区 直接结果 上考虑周期对称性的结果 图式中的第一 >反映能带的全貌 布里渊区
8 2.电子导电:金属 能带的三种表示方法 扩展区图式: ➢ 微扰论计算得到的 直接结果 简约区图式: ➢ 只考虑重复区 图式中的第一 布里渊区 重复区图式: ➢ 在微扰论计算结果的基础 上考虑周期对称性的结果 ➢ 反映能带的全貌
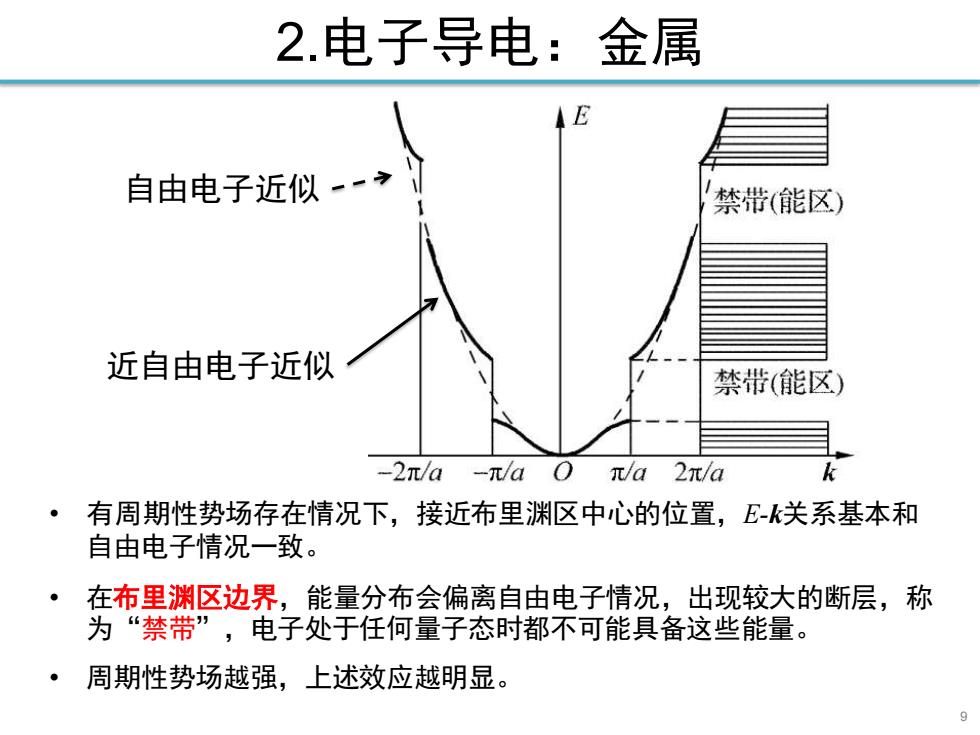
2.电子导电:金属 自由电子近似- 禁带(能区) 近自由电子近似 禁带(能区) -2π/a-π/aO π/a2元/a 有周期性势场存在情况下,接近布里渊区中心的位置,E-k关系基本和 自由电子情况一致。 在布里渊区边界,能量分布会偏离自由电子情况,出现较大的断层,称 为“禁带”,电子处于任何量子态时都不可能具备这些能量。 周期性势场越强,上述效应越明显
2.电子导电:金属 9 自由电子近似 近自由电子近似 • 有周期性势场存在情况下,接近布里渊区中心的位置,E-k关系基本和 自由电子情况一致。 • 在布里渊区边界,能量分布会偏离自由电子情况,出现较大的断层,称 为“禁带”,电子处于任何量子态时都不可能具备这些能量。 • 周期性势场越强,上述效应越明显
2.电子导电:金属 自由电子近似一一 禁带(能区) 近自由电子近似 禁带(能区) -2π/a-元/aO 元/a2π/a h2k2 >实际上在k空间的任何位置,能量取值都是不连续 Ek= 2m 的。 2 k+1-kn=2匹 Na k二N n, ·如果材料尺寸Na足够大,能带内部的能量可以认 n=0,±1,±2, 为是接近连续的。 ·对纳米材料而言,能带内部能量也会严重离散。10
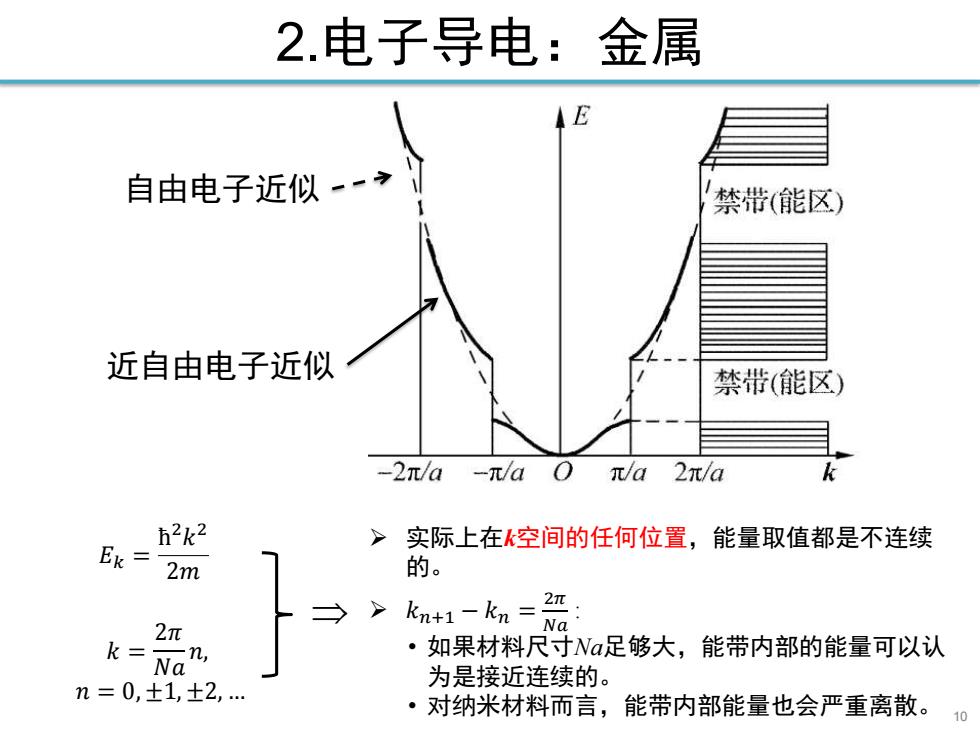
2.电子导电:金属 10 自由电子近似 近自由电子近似 𝐸𝑘 = ħ 2𝑘 2 2𝑚 𝑘 = 2𝜋 𝑁𝑎 𝑛, 𝑛 = 0, ±1, ±2, . ➢ 实际上在k空间的任何位置,能量取值都是不连续 的。 ➢ 𝑘𝑛+1 − 𝑘𝑛 = 2𝜋 𝑁𝑎 : • 如果材料尺寸Na足够大,能带内部的能量可以认 为是接近连续的。 • 对纳米材料而言,能带内部能量也会严重离散