【智能系统】鳍-水舱综合减摇混沌系统控制方法研究

第12卷第3期 智能系统学报 Vol.12 No.3 2017年6月 CAAI Transactions on Intelligent Systems Jun.2017 D0I:10.11992/tis.201607012 网络出版地址：http:/kns.cmki.net/kcms/detail/23.1538.TP.20170401.1541.002.html 鳍-水舱综合减摇混沌系统控制方法研究 王辉，车超，于立君，刘少英，游江 (哈尔滨工程大学自动化学院，黑龙江哈尔滨150001) 摘要：针对船舶减摇问题，对综合减摇系统动力学模型方程进行分析，可知该系统为混沌系统。利用相图与 Lyapunov指数谱分析方法，验证该系统在特定条件下的混沌行为，通过选取合理受控参数，利用非线性反馈控制方 法使系统的混沌行为得到有效控制。该方法使系统混沌动力学行为得到了改善，并保留了系统原有的动力学特性。 将混沌搜索算法与蚁群算法相结合，实现对PD控制参数寻优，使混沌蚁群算法不仅具备较强全局优化能力，与此 同时，系统的收敛速度得到提高，该控制系统的性能得到增强。 关键词：综合减摇系统：参数优化：非线性反馈：混沌搜索算法：蚊群算法：吸引子相同：船舶横摇 中图分类号：TP11文献标志码：A文章编号：1673-4785(2017)03-0318-07 中文引用格式：王辉，车超，于立君，等.鳍-水舱综合减摇混沌系统控制方法研究[J].智能系统学报，2017,12(3)：318-324. 英文引用格式：WANG Hui,CHE Chao,YULijun,etal.Control method for a fin/tank integrated stabilization chaotic system[J]. CAAI transactions on intelligent systems,2017,12(3):318-324. Control method for a fin/tank integrated stabilization chaotic system WANG Hui,CHE Chao,YU Lijun,LIU Shaoying,YOU Jiang College of Automation,Harbin Engineering University,Harbin 150001,China) Abstract:Based on the ship roll problem,the dynamic model equations of an integrated stabilization system were analyzed and proved this to be a chaotic system.The analytical method of phase diagrams and Lyapunov indexes were used to verify the chaotic motion of the system under certain conditions,then a nonlinear feedback control method was used to control this chaotic motion by choosing reasonable control parameters.This method reduced the chaotic motion of the system without destroying the original dynamic characteristics.The chaos search algorithm was combined with an ant colony algorithm to search the best parameters for PID.Therefore,the chaos ant colony optimization algorithm not only had strong global optimization ability but also accelerated the convergence speed.As a result,the performance of the control system was significantly improved. Keywords:integrated stabilization;parameter optimization;nonlinear feedback;chaos search algorithm;colony algorithm;attractor phase diagram;ship roll 船舶的横摇是一个不规则的非线性运动，在非 滑膜变结构控制与自适应控制方法相结合，同时提 线性横摇运动中，混沌现象对船舶的航行有非常大 出单输入自适应变结构控制法对船舶混沌运动进 的影响，混沌运动是导致船舶倾覆的主要原因之 行控制并收到良好效果：胡开业等)，采用随机 一【]。近年来，人们对船舶横摇混沌现象的形成 Melnikov方法分析了在随机横浪中的船舶全局稳定 以及预测做了深入研究，并针对混沌特性设计了不 性，并得出船舶横摇出现混沌运动的条件s-刀。然 同的控制方法。R.F.Mohammad和N.Mehdi等基 而，对于已经配备了减摇鳍和减摇水舱的船舶的横 于混沌嵌入式PSO算法设计分数阶PID控制器，实 摇混沌运动的控制，目前还没有可供遵循的方法。 现了对船舶横摇混沌运动的有效控制：黄谦等[)将 本文运用混沌理论对综合减摇系统（配备减摇 鳍和被动式减摇水舱的船舶系统)动力学方程进行 收稿日期：2016-07-14.网络出版日期：2017-04-01. 混沌行为分析，并采用非线性反馈控制法对系统实 基金项目：国家自然科学基金项目(51479042). 现混沌控制，最后利用混沌蚁群算法对PD控制参 通信作者：于立君.E-mail:yulijun@hrbeu..edu.cn

第 １２ 卷第 ３ 期 智 能 系 统 学 报 Ｖｏｌ．１２ №．３ ２０１７ 年 ６ 月 ＣＡＡＩ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｉｎｔｅｌｌｉｇｅｎｔ Ｓｙｓｔｅｍｓ Ｊｕｎ． ２０１７ ＤＯＩ：１０．１１９９２ ／ ｔｉｓ．２０１６０７０１２ 网络出版地址：ｈｔｔｐ： ／ ／ ｋｎｓ．ｃｎｋｉ．ｎｅｔ ／ ｋｃｍｓ／ ｄｅｔａｉｌ ／ ２３．１５３８．ＴＰ．２０１７０４０１．１５４１．００２．ｈｔｍｌ 鳍－水舱综合减摇混沌系统控制方法研究 王辉， 车超， 于立君， 刘少英， 游江 （哈尔滨工程大学 自动化学院，黑龙江 哈尔滨 １５０００１） 摘 要：针对船舶减摇问题，对综合减摇系统动力学模型方程进行分析，可知该系统为混沌系统。 利用相图与 Ｌｙａｐｕｎｏｖ 指数谱分析方法，验证该系统在特定条件下的混沌行为，通过选取合理受控参数，利用非线性反馈控制方 法使系统的混沌行为得到有效控制。 该方法使系统混沌动力学行为得到了改善，并保留了系统原有的动力学特性。 将混沌搜索算法与蚁群算法相结合，实现对 ＰＩＤ 控制参数寻优，使混沌蚁群算法不仅具备较强全局优化能力，与此 同时，系统的收敛速度得到提高，该控制系统的性能得到增强。 关键词：综合减摇系统；参数优化；非线性反馈；混沌搜索算法；蚁群算法；吸引子相同；船舶横摇 中图分类号：ＴＰ１１ 文献标志码：Ａ 文章编号：１６７３－４７８５（２０１７）０３－０３１８－０７ 中文引用格式：王辉， 车超， 于立君，等． 鳍－水舱综合减摇混沌系统控制方法研究［Ｊ］． 智能系统学报， ２０１７， １２（３）： ３１８－３２４． 英文引用格式：ＷＡＮＧ Ｈｕｉ， ＣＨＥ Ｃｈａｏ， ＹＵ Ｌｉｊｕｎ， ｅｔ ａｌ． Ｃｏｎｔｒｏｌ ｍｅｔｈｏｄ ｆｏｒ ａ ｆｉｎ ／ ｔａｎｋ ｉｎｔｅｇｒａｔｅｄ ｓｔａｂｉｌｉｚａｔｉｏｎ ｃｈａｏｔｉｃ ｓｙｓｔｅｍ［Ｊ］． ＣＡＡＩ ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ ｉｎｔｅｌｌｉｇｅｎｔ ｓｙｓｔｅｍｓ， ２０１７， １２（３）： ３１８－３２４． Ｃｏｎｔｒｏｌ ｍｅｔｈｏｄ ｆｏｒ ａ ｆｉｎ ／ ｔａｎｋ ｉｎｔｅｇｒａｔｅｄ ｓｔａｂｉｌｉｚａｔｉｏｎ ｃｈａｏｔｉｃ ｓｙｓｔｅｍ ＷＡＮＧ Ｈｕｉ， ＣＨＥ Ｃｈａｏ， ＹＵ Ｌｉｊｕｎ， ＬＩＵ Ｓｈａｏｙｉｎｇ， ＹＯＵ Ｊｉａｎｇ （Ｃｏｌｌｅｇｅ ｏｆ Ａｕｔｏｍａｔｉｏｎ， Ｈａｒｂｉｎ Ｅｎｇｉｎｅｅｒｉｎｇ Ｕｎｉｖｅｒｓｉｔｙ， Ｈａｒｂｉｎ １５０００１， Ｃｈｉｎａ） Ａｂｓｔｒａｃｔ：Ｂａｓｅｄ ｏｎ ｔｈｅ ｓｈｉｐ ｒｏｌｌ ｐｒｏｂｌｅｍ， ｔｈｅ ｄｙｎａｍｉｃ ｍｏｄｅｌ ｅｑｕａｔｉｏｎｓ ｏｆ ａｎ ｉｎｔｅｇｒａｔｅｄ ｓｔａｂｉｌｉｚａｔｉｏｎ ｓｙｓｔｅｍ ｗｅｒｅ ａｎａｌｙｚｅｄ ａｎｄ ｐｒｏｖｅｄ ｔｈｉｓ ｔｏ ｂｅ ａ ｃｈａｏｔｉｃ ｓｙｓｔｅｍ．Ｔｈｅ ａｎａｌｙｔｉｃａｌ ｍｅｔｈｏｄ ｏｆ ｐｈａｓｅ ｄｉａｇｒａｍｓ ａｎｄ Ｌｙａｐｕｎｏｖ ｉｎｄｅｘｅｓ ｗｅｒｅ ｕｓｅｄ ｔｏ ｖｅｒｉｆｙ ｔｈｅ ｃｈａｏｔｉｃ ｍｏｔｉｏｎ ｏｆ ｔｈｅ ｓｙｓｔｅｍ ｕｎｄｅｒ ｃｅｒｔａｉｎ ｃｏｎｄｉｔｉｏｎｓ， ｔｈｅｎ ａ ｎｏｎｌｉｎｅａｒ ｆｅｅｄｂａｃｋ ｃｏｎｔｒｏｌ ｍｅｔｈｏｄ ｗａｓ ｕｓｅｄ ｔｏ ｃｏｎｔｒｏｌ ｔｈｉｓ ｃｈａｏｔｉｃ ｍｏｔｉｏｎ ｂｙ ｃｈｏｏｓｉｎｇ ｒｅａｓｏｎａｂｌｅ ｃｏｎｔｒｏｌ ｐａｒａｍｅｔｅｒｓ． Ｔｈｉｓ ｍｅｔｈｏｄ ｒｅｄｕｃｅｄ ｔｈｅ ｃｈａｏｔｉｃ ｍｏｔｉｏｎ ｏｆ ｔｈｅ ｓｙｓｔｅｍ ｗｉｔｈｏｕｔ ｄｅｓｔｒｏｙｉｎｇ ｔｈｅ ｏｒｉｇｉｎａｌ ｄｙｎａｍｉｃ ｃｈａｒａｃｔｅｒｉｓｔｉｃｓ．Ｔｈｅ ｃｈａｏｓ ｓｅａｒｃｈ ａｌｇｏｒｉｔｈｍ ｗａｓ ｃｏｍｂｉｎｅｄ ｗｉｔｈ ａｎ ａｎｔ ｃｏｌｏｎｙ ａｌｇｏｒｉｔｈｍ ｔｏ ｓｅａｒｃｈ ｔｈｅ ｂｅｓｔ ｐａｒａｍｅｔｅｒｓ ｆｏｒ ＰＩＤ． Ｔｈｅｒｅｆｏｒｅ， ｔｈｅ ｃｈａｏｓ ａｎｔ ｃｏｌｏｎｙ ｏｐｔｉｍｉｚａｔｉｏｎ ａｌｇｏｒｉｔｈｍ ｎｏｔ ｏｎｌｙ ｈａｄ ｓｔｒｏｎｇ ｇｌｏｂａｌ ｏｐｔｉｍｉｚａｔｉｏｎ ａｂｉｌｉｔｙ ｂｕｔ ａｌｓｏ ａｃｃｅｌｅｒａｔｅｄ ｔｈｅ ｃｏｎｖｅｒｇｅｎｃｅ ｓｐｅｅｄ． Ａｓ ａ ｒｅｓｕｌｔ， ｔｈｅ ｐｅｒｆｏｒｍａｎｃｅ ｏｆ ｔｈｅ ｃｏｎｔｒｏｌ ｓｙｓｔｅｍ ｗａｓ ｓｉｇｎｉｆｉｃａｎｔｌｙ ｉｍｐｒｏｖｅｄ． Ｋｅｙｗｏｒｄｓ： ｉｎｔｅｇｒａｔｅｄ ｓｔａｂｉｌｉｚａｔｉｏｎ； ｐａｒａｍｅｔｅｒ ｏｐｔｉｍｉｚａｔｉｏｎ； ｎｏｎｌｉｎｅａｒ ｆｅｅｄｂａｃｋ； ｃｈａｏｓ ｓｅａｒｃｈ ａｌｇｏｒｉｔｈｍ； ｃｏｌｏｎｙ ａｌｇｏｒｉｔｈｍ； ａｔｔｒａｃｔｏｒ ｐｈａｓｅ ｄｉａｇｒａｍ； ｓｈｉｐ ｒｏｌｌ 收稿日期：２０１６－０７－１４． 网络出版日期：２０１７－０４－０１． 基金项目：国家自然科学基金项目（５１４７９０４２）． 通信作者：于立君． Ｅ⁃ｍａｉｌ： ｙｕｌｉｊｕｎ＠ ｈｒｂｅｕ．ｅｄｕ．ｃｎ． 船舶的横摇是一个不规则的非线性运动，在非 线性横摇运动中，混沌现象对船舶的航行有非常大 的影响，混沌运动是导致船舶倾覆的主要原因之 一［１－４］ 。 近年来，人们对船舶横摇混沌现象的形成 以及预测做了深入研究，并针对混沌特性设计了不 同的控制方法。 Ｒ．Ｆ．Ｍｏｈａｍｍａｄ 和 Ｎ． Ｍｅｈｄｉ 等［１］基 于混沌嵌入式 ＰＳＯ 算法设计分数阶 ＰＩＤ 控制器，实 现了对船舶横摇混沌运动的有效控制；黄谦等［６］ 将 滑膜变结构控制与自适应控制方法相结合，同时提 出单输入自适应变结构控制法对船舶混沌运动进 行控制并收到良好效果；胡开业等［７］ ， 采用随机 Ｍｅｌｎｉｋｏｖ 方法分析了在随机横浪中的船舶全局稳定 性，并得出船舶横摇出现混沌运动的条件［５－７］ 。 然 而，对于已经配备了减摇鳍和减摇水舱的船舶的横 摇混沌运动的控制，目前还没有可供遵循的方法。 本文运用混沌理论对综合减摇系统（配备减摇 鳍和被动式减摇水舱的船舶系统）动力学方程进行 混沌行为分析，并采用非线性反馈控制法对系统实 现混沌控制，最后利用混沌蚁群算法对 ＰＩＤ 控制参

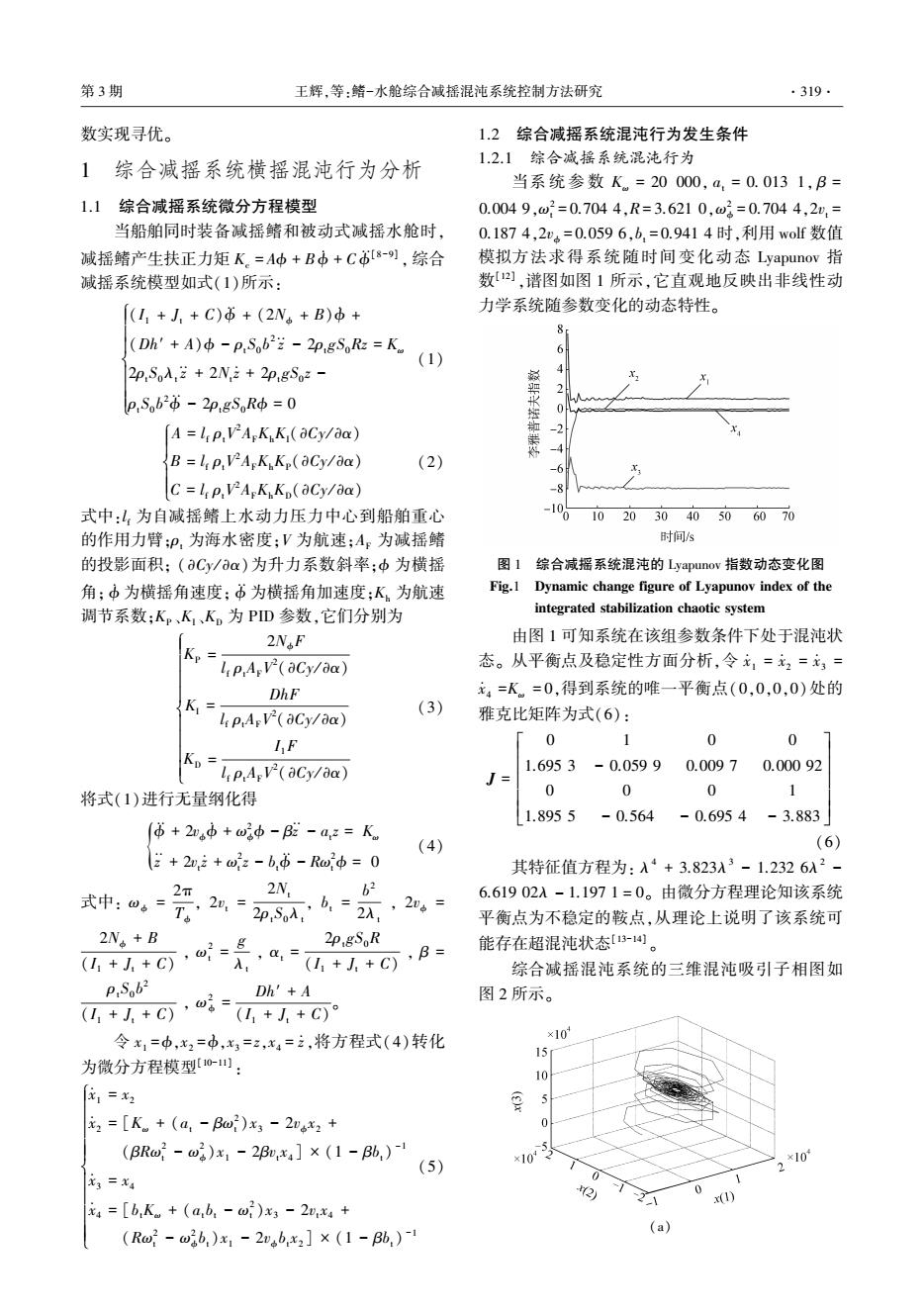
第3期 王辉，等：鳍-水舱综合减摇混沌系统控制方法研究 ·319· 数实现寻优。 1.2综合减摇系统混沌行为发生条件 1综合减摇系统横摇混沌行为分析 1.2.1综合减摇系统混沌行为 当系统参数K。=20000,a.=0.0131,B= 1.1综合减摇系统微分方程模型 0.0049,w2=0.7044,R=3.6210,w2=0.7044,2,= 当船舶同时装备减摇鳍和被动式减摇水舱时， 0.1874,2m。=0.0596,b,=0.9414时，利用wolf数值 减摇鳍产生扶正力矩K。=A中+B中+C8-),综合 模拟方法求得系统随时间变化动态Lyapunov指 减摇系统模型如式(1)所示： 数2]，谱图如图1所示，它直观地反映出非线性动 (I1+J,+C)本+(2N。+B)中+ 力学系统随参数变化的动态特性。 (Dh'+A)-p,Sob2-2p:gSoRz=K (1) 6 2p,So入，2+2N2+2p,gSo2- A p,Sob2d-2p:gSoRo =0 A =Lp,V-AgK K (aCy/aa) 2 B=lp,V-AK Kp(aCy/aa) (2) -6 C=Ip,VA K Kp(aCy/aa) -8 式中：山为自减摇鳍上水动力压力中心到船舶重心 -106 10203040506070 的作用力臂：P,为海水密度；V为航速；A,为减摇鳍 时间s 的投影面积；(aCy/aa)为升力系数斜率：中为横摇 图1综合减摇系统混沌的Lyapunov指数动态变化图 角；本为横摇角速度：$为横摇角加速度；K为航速 Fig.1 Dynamic change figure of Lyapunov index of the 调节系数：Kp、KK。为PID参数，它们分别为 integrated stabilization chaotic system 2NF 由图1可知系统在该组参数条件下处于混沌状 Kp lp,A2(aCy/aa） 态。从平衡点及稳定性方面分析，令元1=2=3= DhF 元4=K=0,得到系统的唯一平衡点(0,0,0,0)处的 K= lpArV(aCy/aa) (3) 雅克比矩阵为式(6)： IF 0 0 0 KD= lP,ArV(aCy/aa) 1.6953-0.0599 0.0097 0.00092 将式(1)进行无量纲化得 0 0 0 1.8955 -0.564 -0.6954-3.883 $+2中+w2中-B2-a,z=K (4) (6) E+2,2+w2-b,6-Rwb=0 其特征值方程为：入4+3.823A3-1.2326入2- 2N. b2 式中，m=2T,2m,=20S入，6=2入，2gs 6.61902入-1.1971=0。由微分方程理论知该系统 平衡点为不稳定的鞍点，从理论上说明了该系统可 2N。+B (4+1+C,a=点， 2p.gSoR (山++C),B= 能存在超混沌状态3=。 综合减摇混沌系统的三维混沌吸引子相图如 P:So62 Dh'+A (4+人+C),w8= 图2所示。 (1+J,+C)9 令x1=中，x2=中，x=z,x4=立，将方程式(4)转化 ×10 15r 为微分方程模型0)： 10 x1=X2 5 元2=[K+(a,-Bω)x3-2x2+ 0 (BRω-ω3)x1-2B,x4]×(1-B6,)- ×103 ×10 (5) x3=x4 0 2) dT) 元4=[b,Kw+(a,b,-w)x3-2,x4+ (Rω-w3b,)x1-2mbx2]×(1-Bb,)

数实现寻优。 １ 综合减摇系统横摇混沌行为分析 １．１ 综合减摇系统微分方程模型 当船舶同时装备减摇鳍和被动式减摇水舱时， 减摇鳍产生扶正力矩 Ｋｃ ＝ Ａϕ ＋ Ｂ ϕ · ＋ Ｃ ϕ ··［８－９］ ， 综合 减摇系统模型如式（１）所示： （Ｉ１ ＋ Ｊｔ ＋ Ｃ）ϕ ·· ＋ （２Ｎϕ ＋ Ｂ）ϕ · ＋ （Ｄｈ′ ＋ Ａ）ϕ － ρｔＳ０ ｂ ２ ｚ ·· － ２ρｔｇＳ０Ｒｚ ＝ Ｋω ２ρｔＳ０λｔ ｚ ·· ＋ ２Ｎｔ ｚ · ＋ ２ρｔｇＳ０ ｚ － ρｔＳ０ ｂ ２ϕ ·· － ２ρｔｇＳ０Ｒϕ ＝ ０ ì î í ï ï ï ï ï ï （１） Ａ ＝ ｌ ｆ ρｔＶ ２ ＡＦＫｈＫＩ（∂Ｃｙ ／ ∂α） Ｂ ＝ ｌ ｆ ρｔＶ ２ ＡＦＫｈＫＰ（∂Ｃｙ ／ ∂α） Ｃ ＝ ｌ ｆ ρｔＶ ２ ＡＦＫｈＫＤ（∂Ｃｙ ／ ∂α） ì î í ï ï ï ï （２） 式中：ｌ ｆ 为自减摇鳍上水动力压力中心到船舶重心 的作用力臂；ρｔ 为海水密度；Ｖ 为航速；ＡＦ 为减摇鳍 的投影面积； （∂Ｃｙ ／ ∂α）为升力系数斜率；ϕ 为横摇 角； ϕ · 为横摇角速度； ϕ ··为横摇角加速度；Ｋｈ 为航速 调节系数；ＫＰ 、ＫＩ、ＫＤ 为 ＰＩＤ 参数，它们分别为 ＫＰ ＝ ２ＮϕＦ ｌ ｆ ρｔＡＦ Ｖ ２ （∂Ｃｙ ／ ∂α） ＫＩ ＝ ＤｈＦ ｌ ｆ ρｔＡＦ Ｖ ２ （∂Ｃｙ ／ ∂α） ＫＤ ＝ Ｉ１Ｆ ｌ ｆ ρｔＡＦ Ｖ ２ （∂Ｃｙ ／ ∂α） ì î í ï ï ï ï ï ï ï ï （３） 将式（１）进行无量纲化得 ϕ ·· ＋ ２ｖϕϕ · ＋ ω ２ ϕϕ － βｚ ·· － ａｔ ｚ ＝ Ｋω ｚ ·· ＋ ２ｖｔ ｚ · ＋ ω ２ ｔ ｚ － ｂｔϕ ·· － Ｒω ２ { ｔ ϕ ＝ ０ （４） 式中： ωϕ ＝ ２π Ｔϕ ， ２ｖｔ ＝ ２Ｎｔ ２ρｔＳ０λｔ ， ｂｔ ＝ ｂ ２ ２λｔ ， ２ｖϕ ＝ ２Ｎϕ ＋ Ｂ （Ｉ１ ＋ Ｊｔ ＋ Ｃ） ， ω ２ ｔ ＝ ｇ λｔ ， αｔ ＝ ２ρｔｇＳ０Ｒ （Ｉ１ ＋ Ｊｔ ＋ Ｃ） ， β ＝ ρｔＳ０ ｂ ２ （Ｉ１ ＋ Ｊｔ ＋ Ｃ） ， ω ２ ϕ ＝ Ｄｈ′ ＋ Ａ （Ｉ１ ＋ Ｊｔ ＋ Ｃ） 。 令 ｘ１ ＝ϕ，ｘ２ ＝ϕ · ，ｘ３ ＝ ｚ，ｘ４ ＝ ｚ · ，将方程式（４）转化 为微分方程模型［１０－１１］ ： ｘ · １ ＝ ｘ２ ｘ · ２ ＝ ［Ｋω ＋ （ａｔ － βω ２ ｔ ）ｘ３ － ２ｖϕ ｘ２ ＋ （βＲω ２ ｔ － ω ２ ϕ）ｘ１ － ２βｖｔ ｘ４ ］ × （１ － βｂｔ） －１ ｘ · ３ ＝ ｘ４ ｘ · ４ ＝ ［ｂｔＫω ＋ （ａｔ ｂｔ － ω ２ ｔ ）ｘ３ － ２ｖｔ ｘ４ ＋ （Ｒω ２ ｔ － ω ２ ϕ ｂｔ）ｘ１ － ２ｖϕ ｂｔ ｘ２ ］ × （１ － βｂｔ） －１ ì î í ï ï ï ï ï ï ï ï ïï （５） １．２ 综合减摇系统混沌行为发生条件 １．２．１ 综合减摇系统混沌行为 当系 统 参 数 Ｋω ＝ ２０ ０００， ａｔ ＝ ０． ０１３ １， β ＝ ０．００４ ９，ω ２ ｔ ＝ ０．７０４ ４，Ｒ ＝ ３．６２１ ０，ω ２ ϕ ＝ ０．７０４ ４，２ｖｔ ＝ ０．１８７ ４，２ｖϕ ＝ ０．０５９ ６，ｂｔ ＝ ０．９４１ ４ 时，利用 ｗｏｌｆ 数值 模拟方法求得系统随时间变化动态 Ｌｙａｐｕｎｏｖ 指 数［１２］ ，谱图如图 １ 所示，它直观地反映出非线性动 力学系统随参数变化的动态特性。 图 １ 综合减摇系统混沌的 Ｌｙａｐｕｎｏｖ 指数动态变化图 Ｆｉｇ．１ Ｄｙｎａｍｉｃ ｃｈａｎｇｅ ｆｉｇｕｒｅ ｏｆ Ｌｙａｐｕｎｏｖ ｉｎｄｅｘ ｏｆ ｔｈｅ ｉｎｔｅｇｒａｔｅｄ ｓｔａｂｉｌｉｚａｔｉｏｎ ｃｈａｏｔｉｃ ｓｙｓｔｅｍ 由图 １ 可知系统在该组参数条件下处于混沌状 态。 从平衡点及稳定性方面分析，令 ｘ · １ ＝ ｘ · ２ ＝ ｘ · ３ ＝ ｘ · ４ ＝Ｋω ＝ ０，得到系统的唯一平衡点（０，０，０，０）处的 雅克比矩阵为式（６）： Ｊ ＝ ０ １ ０ ０ １．６９５ ３ － ０．０５９ ９ ０．００９ ７ ０．０００ ９２ ０ ０ ０ １ １．８９５ ５ － ０．５６４ － ０．６９５ ４ － ３．８８３ é ë ê ê ê ê ê ù û ú ú ú ú ú （６） 其特征值方程为： λ ４ ＋ ３．８２３λ ３ － １．２３２ ６λ ２ － ６．６１９ ０２λ － １．１９７ １ ＝ ０。 由微分方程理论知该系统 平衡点为不稳定的鞍点，从理论上说明了该系统可 能存在超混沌状态［１３－１４］ 。 综合减摇混沌系统的三维混沌吸引子相图如 图 ２ 所示。 （ａ） 第 ３ 期 王辉，等：鳍－水舱综合减摇混沌系统控制方法研究 ·３１９·

.320 智能系统学报 第12卷 ×10 6 1=x2 4 x2=[K。+(a,-Bw)x3-2Bu,x4+ 2 要 (BRm-wi)x1-2x2]×(1-B6)1+K2x2 -2 =X4 -4 元4=(bK。+(a,b.-ω)x3-2,x4+ x1015 (Ra-mdb,)x1-2mbx2）×(1-B6,)- 10 2x10 (7) r3) 0-5 01) 式中K为系统的分岔参数。图4是受控系统在参 数K下的Lyapunov指数图。 (b) ×10 150 6 100 4 0 0 -2 -5 200 ×10 1 2*10 100 3 0 50100150 x1) 2 -12 0 10-500 x1) (a) (c) ×103 4 60 2 0 20 -2 -4 -20 -6 *105 10 00 100 10 2 50 100150 1 0 2) 0 3) 0 100-50 (1) -52 x(2) (b) (d) 图2综合减摇混沌系统的三维混沌吸引子相图 Fig.2 Three-dimensional chaotic attractor phase diagram of integrated stabilization chaotic system 1.22非线性反馈控制下混沌行为 40 利用分段二次函数x|xI作为产生混沌的发生 20 器，选择合适分岔K参数作该混沌系统非线性反馈 0 -2 控制器，并应用于非线性系统中进行反馈操作，使 系统寻找不稳定周期轨道同时实现混沌系统的有 150100 150 50 100 效控制s-)。对系统式(5)进行混沌控制，把反馈 3) 0 5050 0 1) 控制器代入式(5)得到系统方程(7)，系统参数不 (c) 变，则综合减摇混沌系统的混沌子相图如图3所示。 80 60 -5 40 10 9 0 -15 - 150100 200 20 50 100 3) 0 50-100 0 x(2) 0 6810 (d) 2 4 图4 非线性反馈控制后综合减摇混沌系统的三维混沌 子相图 图3 Lyapunov指数随K变化曲线 Fig.4 Three-dimensional chaotic attractor phase Fig.3 Graph of the Lyapunov index with the change of K diagram after nonlinear feedback control

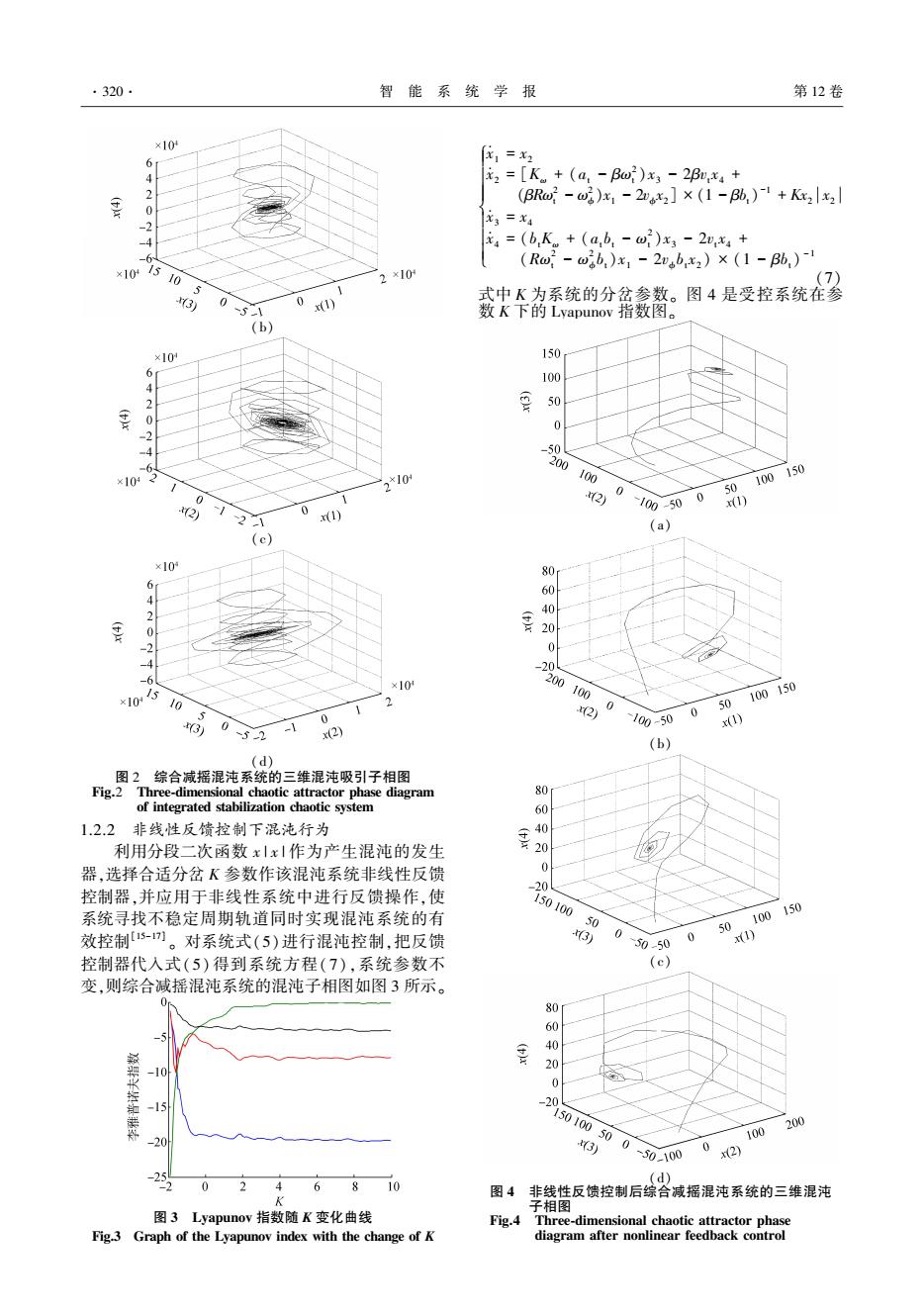
（ｂ） （ｃ） （ｄ） 图 ２ 综合减摇混沌系统的三维混沌吸引子相图 Ｆｉｇ．２ Ｔｈｒｅｅ⁃ｄｉｍｅｎｓｉｏｎａｌ ｃｈａｏｔｉｃ ａｔｔｒａｃｔｏｒ ｐｈａｓｅ ｄｉａｇｒａｍ ｏｆ ｉｎｔｅｇｒａｔｅｄ ｓｔａｂｉｌｉｚａｔｉｏｎ ｃｈａｏｔｉｃ ｓｙｓｔｅｍ １．２．２ 非线性反馈控制下混沌行为 利用分段二次函数 ｘ ｜ ｘ ｜ 作为产生混沌的发生 器，选择合适分岔 Ｋ 参数作该混沌系统非线性反馈 控制器，并应用于非线性系统中进行反馈操作，使 系统寻找不稳定周期轨道同时实现混沌系统的有 效控制［１５－１７］ 。 对系统式（５）进行混沌控制，把反馈 控制器代入式（５） 得到系统方程（７），系统参数不 变，则综合减摇混沌系统的混沌子相图如图 ３ 所示。 图 ３ Ｌｙａｐｕｎｏｖ 指数随 Ｋ 变化曲线 Ｆｉｇ．３ Ｇｒａｐｈ ｏｆ ｔｈｅ Ｌｙａｐｕｎｏｖ ｉｎｄｅｘ ｗｉｔｈ ｔｈｅ ｃｈａｎｇｅ ｏｆ Ｋ ｘ · １ ＝ ｘ２ ｘ · ２ ＝ ［Ｋω ＋ （ａｔ － βω ２ ｔ ）ｘ３ － ２βｖｔ ｘ４ ＋ （βＲω ２ ｔ － ω ２ ϕ）ｘ１ － ２ｖϕ ｘ２］ × （１ － βｂｔ） －１ ＋ Ｋｘ２ ｘ２ ｘ · ３ ＝ ｘ４ ｘ · ４ ＝ （ｂｔＫω ＋ （ａｔ ｂｔ － ω ２ ｔ ）ｘ３ － ２ｖｔ ｘ４ ＋ （Ｒω ２ ｔ － ω ２ ϕ ｂｔ）ｘ１ － ２ｖϕ ｂｔ ｘ２ ） × （１ － βｂｔ） －１ ì î í ï ï ï ï ï ï （７） 式中 Ｋ 为系统的分岔参数。 图 ４ 是受控系统在参 数 Ｋ 下的 Ｌｙａｐｕｎｏｖ 指数图。 （ａ） （ｂ） （ｃ） （ｄ） 图 ４ 非线性反馈控制后综合减摇混沌系统的三维混沌 子相图 Ｆｉｇ．４ Ｔｈｒｅｅ⁃ｄｉｍｅｎｓｉｏｎａｌ ｃｈａｏｔｉｃ ａｔｔｒａｃｔｏｒ ｐｈａｓｅ ｄｉａｇｒａｍ ａｆｔｅｒ ｎｏｎｌｉｎｅａｒ ｆｅｅｄｂａｃｋ ｃｏｎｔｒｏｌ ·３２０· 智 能 系 统 学 报 第 １２ 卷

第3期 王辉，等：鳍-水舱综合减摇混沌系统控制方法研究 ·321· 由图4可知，当K∈[-24]时，系统的Lyapunov 2.2 混沌蚊群算法对综合减摇系统PID参数优化 指数都非正，系统一直处于周期态；当K>4时，系统 将混沌蚁群优化算法应用于综合减摇系统PID 进入混沌态。图3给出了系统在分岔参数K=2值 控制器2的优化原理方框图如图6所示。 下的三维相图。从图3可得：系统处于周期态，而非 海浪波倾角 PID 船舶减摇横摇角 混沌运动，故选择当Lyapunov指数为负时所对应的 控制器 模型 K值可有效控制系统的混沌行为。 混沌蚁群 寻优算法 2混沌蚁群算法的综合减摇系统PID M文件 控制参数寻优 图6混沌蚊群算法优化原理图 2.1混沌蚊群优化算法 Fig.6 Optimization schematic of chaos 利用网格划分策略将离散优化蚁群算法思想应用 ant colony algorithm 到连续函数优化的问题，有很多不足之处。例如：搜索 利用混沌蚁群算法优化控制器PID参数的主 时间和范围与遗传算法相比，该算法搜索时间较长，易 要步骤依次为： 出现局部最优，发生停滞，其对最优解的寻找不易实 1)PID控制参数优化问题转化为蚁群算法适用 现-0。本文将蚁群算法与混沌优化算法有机结合， 的组合优化问题 应用于PD控制参数寻优问题，不仅可以避免搜素过 首先把控制器的控制参数Kp、K、K。转换为一 程中停滞现象，同时还可以解决搜索效率低的问题。 个组合寻优的问题，在满足控制精度要求情况下， 具有混沌特性蚁群算法搜索过程可分为两个步骤：首 可将控制参数值视为5位有效数字，所以待寻参数 先，利用混沌搜索算法初步确定最优解所在范围的 (Kp、K、Kn)组成15位的数字序列记为{c,i=1, 大小：然后，在确定最优蚂蚁基础上再利用混沌算 2,…,15},每个c:取值为y{=1,2,…,9},因此每 法进行寻优，若满足终止条件，则获得最优解。混 次序列可以在{(c,y)i=1,2,…,15;j=1,2,…, 沌蚁群算法流程如图5所示。 9}组成区域中表示，即这个序列就是人工蚂蚁的一 开始○ 条路径。 初始化迭代次数蚂蚁个数 2)目标函数的建立 为保证控制器具有良好的性能，必须选择合适 搜索优化变量 的目标函数，因此采用改进TAE性能指标作为目 更新信息表和路径 标函数。 利用蚁群算法搜索 ()-x()ld, y(t)≥(t) ITAE 混沌算法进行全局搜索 ly(t)-x(t)dt, y(t)<x(t) 是否优于 (8) 当前值 式中p为调节因子，一般p大于1，可根据实际问题 替换当前最优值 适当调整。 3)路径的构建 蚂蚁搜索 路径的构建是蚁群算法研究中的关键环节，当 全部结束 蚂蚁从(c-1,y)爬行到下一个(c,y)节点按照随机 Y 比例概率进行选择，当所有蚂蚁到达(15，y:)即实现 更新信息表 一次循环。在此过程中，假设蚂蚁此过程中爬行相 全局迭代 邻节点所用时间是相等的，与路径无关。则蚂蚁从 搜索结束 (c-1y)爬行到下一个(c,y)节点按式(9)计算选 输出最优值 择路径的概率： (ciy,t)n(ciyt) 图5混沌蚁群算法流程图 P(ci,yi,t)=- (9) Fig.5 Flow chart of chaos ant colony algorithm re0te场

由图 ４ 可知，当 Ｋ∈［－２ ４］时，系统的 Ｌｙａｐｕｎｏｖ 指数都非正，系统一直处于周期态；当 Ｋ＞４ 时，系统 进入混沌态。 图 ３ 给出了系统在分岔参数 Ｋ ＝ ２ 值 下的三维相图。 从图 ３ 可得：系统处于周期态，而非 混沌运动，故选择当 Ｌｙａｐｕｎｏｖ 指数为负时所对应的 Ｋ 值可有效控制系统的混沌行为。 ２ 混沌蚁群算法的综合减摇系统 ＰＩＤ 控制参数寻优 ２．１ 混沌蚁群优化算法 利用网格划分策略将离散优化蚁群算法思想应用 到连续函数优化的问题，有很多不足之处。 例如：搜索 时间和范围与遗传算法相比，该算法搜索时间较长，易 出现局部最优，发生停滞，其对最优解的寻找不易实 现［１８－２０］ 。 本文将蚁群算法与混沌优化算法有机结合， 应用于 ＰＩＤ 控制参数寻优问题，不仅可以避免搜素过 程中停滞现象，同时还可以解决搜索效率低的问题。 具有混沌特性蚁群算法搜索过程可分为两个步骤：首 先，利用混沌搜索算法初步确定最优解所在范围的 大小；然后，在确定最优蚂蚁基础上再利用混沌算 法进行寻优，若满足终止条件，则获得最优解。 混 沌蚁群算法流程如图 ５ 所示。 图 ５ 混沌蚁群算法流程图 Ｆｉｇ．５ Ｆｌｏｗ ｃｈａｒｔ ｏｆ ｃｈａｏｓ ａｎｔ ｃｏｌｏｎｙ ａｌｇｏｒｉｔｈｍ ２．２ 混沌蚁群算法对综合减摇系统 ＰＩＤ 参数优化 将混沌蚁群优化算法应用于综合减摇系统 ＰＩＤ 控制器［２１］的优化原理方框图如图 ６ 所示。 图 ６ 混沌蚁群算法优化原理图 Ｆｉｇ．６ Ｏｐｔｉｍｉｚａｔｉｏｎ ｓｃｈｅｍａｔｉｃ ｏｆ ｃｈａｏｓ ａｎｔ ｃｏｌｏｎｙ ａｌｇｏｒｉｔｈｍ 利用混沌蚁群算法优化控制器 ＰＩＤ 参数的主 要步骤依次为： １）ＰＩＤ 控制参数优化问题转化为蚁群算法适用 的组合优化问题 首先把控制器的控制参数 ＫＰ 、ＫＩ、ＫＤ 转换为一 个组合寻优的问题，在满足控制精度要求情况下， 可将控制参数值视为 ５ 位有效数字，所以待寻参数 （ＫＰ 、ＫＩ、ＫＤ ） 组成 １５ 位的数字序列记为｛ ｃｉ，ｉ ＝ １， ２，…，１５｝，每个 ｃｉ 取值为 ｙｊ ｛ｊ ＝ １，２，…，９｝，因此每 次序列可以在｛（ ｃｉ，ｙｊ ） ｉ ＝ １，２，…，１５；ｊ ＝ １，２，…， ９｝组成区域中表示，即这个序列就是人工蚂蚁的一 条路径。 ２）目标函数的建立 为保证控制器具有良好的性能，必须选择合适 的目标函数，因此采用改进 ＩＴＡＥ 性能指标作为目 标函数。 ＩＴＡＥ ＝ ∫ ｔ ｉ ０ ｙ（ｔ） － ｙ∗ｐ（ｔ） ｄｔ， ｙ（ｔ） ≥ ｙ∗ｐ（ｔ） ∫ ｔ ｉ ０ ｙ（ｔ） － ｙ∗ｐ（ｔ） ｄｔ， ｙ（ｔ） ＜ ｙ∗ｐ（ｔ） ì î í ï ï ï ï （８） 式中 ｐ 为调节因子，一般 ｐ 大于 １，可根据实际问题 适当调整。 ３）路径的构建 路径的构建是蚁群算法研究中的关键环节，当 蚂蚁从（ｃｉ－１ ，ｙｊ）爬行到下一个（ｃｉ，ｙｊ）节点按照随机 比例概率进行选择，当所有蚂蚁到达（１５，ｙｊ）即实现 一次循环。 在此过程中，假设蚂蚁此过程中爬行相 邻节点所用时间是相等的，与路径无关。 则蚂蚁从 （ｃｉ－１ ，ｙｊ）爬行到下一个（ ｃｉ，ｙｊ）节点按式（９）计算选 择路径的概率： Ｐｋ（ｃｉ，ｙｊ，ｔ） ＝ τ ａ （ｃｉ，ｙｊ，ｔ）η β （ｃｉ，ｙｊ，ｔ） ∑ ９ ｊ ＝ ０ τ ａ （ｃｉ，ｙｊ，ｔ）η β （ｃｉ，ｙｊ，ｔ） （９） 第 ３ 期 王辉，等：鳍－水舱综合减摇混沌系统控制方法研究 ·３２１·

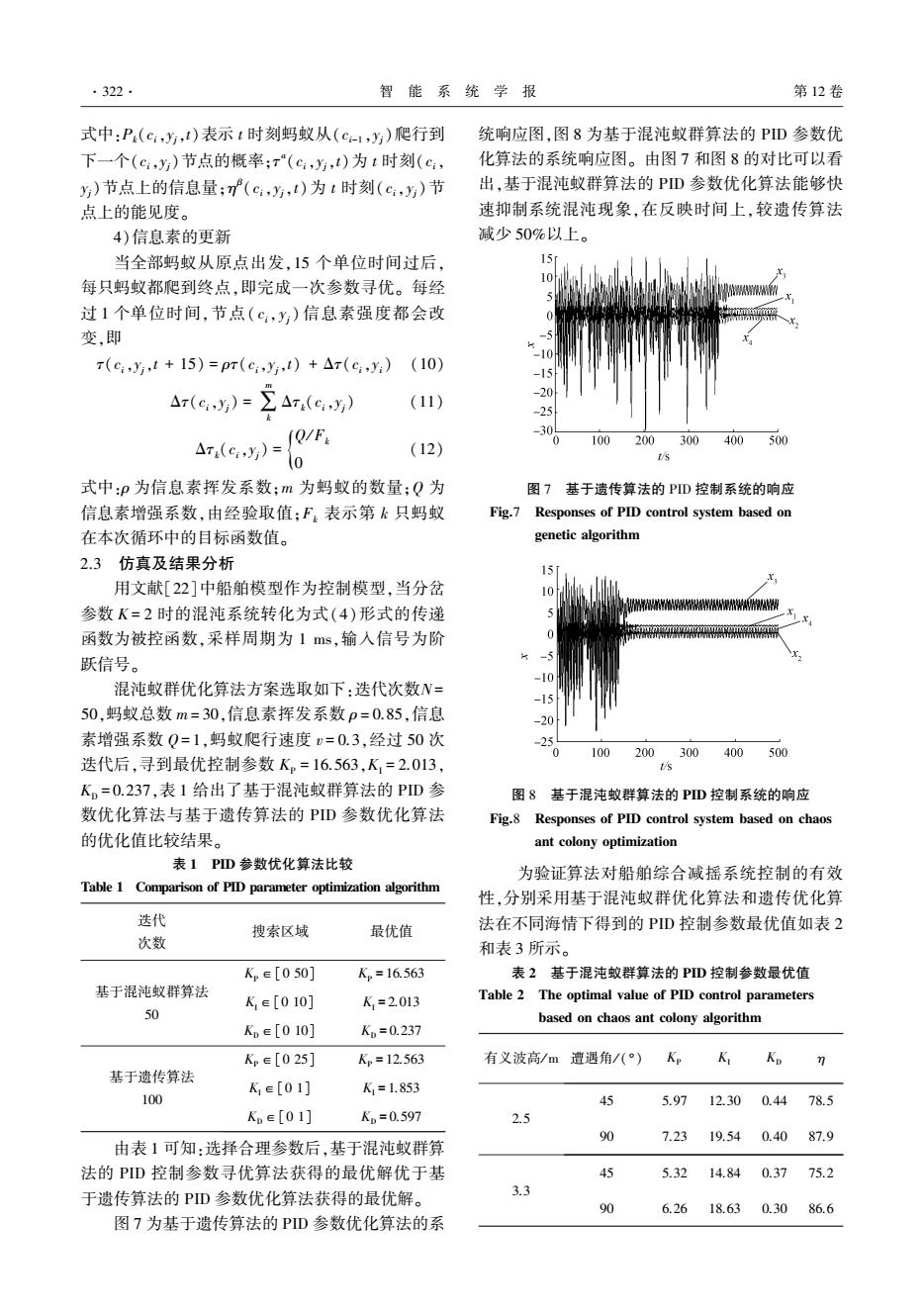
.322. 智能系统学报 第12卷 式中：P(c,y,t)表示t时刻蚂蚁从(c-1,y)爬行到 统响应图，图8为基于混沌蚁群算法的PD参数优 下一个(c,y)节点的概率；r(c,y,t)为t时刻(c, 化算法的系统响应图。由图7和图8的对比可以看 y)节点上的信息量；(c,y,t)为t时刻(c,y)节 出，基于混沌蚁群算法的PD参数优化算法能够快 点上的能见度。 速抑制系统混沌现象，在反映时间上，较遗传算法 4)信息素的更新 减少50%以上。 当全部蚂蚁从原点出发，15个单位时间过后， 每只蚂蚁都爬到终点，即完成一次参数寻优。每经 10 过1个单位时间，节点(c,y,)信息素强度都会改 变，即 10 T(c,y,t+15)=pr(cy,t)+△r(c,y:)(10) △rey)=∑A(e) -20 (11) (Q/F -30 100 200300400500 AT(c,y）= (12) 0 式中：p为信息素挥发系数；m为蚂蚁的数量；Q为 图7基于遗传算法的PD控制系统的响应 信息素增强系数，由经验取值：F表示第k只蚂蚁 Fig.7 Responses of PID control system based on 在本次循环中的目标函数值。 genetic algorithm 2.3仿真及结果分析 用文献[22]中船舶模型作为控制模型，当分岔 参数K=2时的混沌系统转化为式(4)形式的传递 WW 函数为被控函数，采样周期为1ms,输入信号为阶 跃信号。 -10 混沌蚁群优化算法方案选取如下：迭代次数N= -15 50,蚂蚁总数m=30,信息素挥发系数p=0.85,信息 -20 素增强系数Q=1,蚂蚁爬行速度v=0.3,经过50次 25 0 100 200300400500 迭代后，寻到最优控制参数K,=16.563,K=2.013, Kp=0.237,表1给出了基于混沌蚁群算法的PID参 图8基于混沌蚊群算法的PD控制系统的响应 数优化算法与基于遗传算法的PD参数优化算法 Fig.8 Responses of PID control system based on chaos 的优化值比较结果。 ant colony optimization 表1PD参数优化算法比较 为验证算法对船舶综合减摇系统控制的有效 Table 1 Comparison of PID parameter optimization algorithm 性，分别采用基于混沌蚁群优化算法和遗传优化算 迭代 搜索区域 最优值 法在不同海情下得到的PD控制参数最优值如表2 次数 和表3所示。 K,e[050] K。=16.563 表2基于混沌蚊群算法的PD控制参数最优值 基于混沌蚁群算法 K,e[010] K=2.013 Table 2 The optimal value of PID control parameters 50 based on chaos ant colony algorithm K,∈[010] KD=0.237 Kpe[025] Kp=12.563 有义波高/m遭遇角/（°） 7 基于遗传算法 Ke[01] K=1.853 100 45 5.97 12.300.44 78.5 Ko∈[01] K.=0.597 2.5 90 7.23 19.540.40 87.9 由表1可知：选择合理参数后，基于混沌蚁群算 法的PD控制参数寻优算法获得的最优解优于基 45 5.32 14.840.37 75.2 于遗传算法的PD参数优化算法获得的最优解。 3.3 90 6.26 18.63 0.30 86.6 图7为基于遗传算法的PID参数优化算法的系

式中：Ｐｋ（ｃｉ，ｙｊ，ｔ）表示 ｔ 时刻蚂蚁从（ｃｉ－１ ，ｙｊ）爬行到 下一个（ｃｉ，ｙｊ）节点的概率；τ ａ （ｃｉ，ｙｊ，ｔ）为 ｔ 时刻（ｃｉ， ｙｊ）节点上的信息量；η β （ ｃｉ，ｙｊ，ｔ）为 ｔ 时刻（ ｃｉ，ｙｊ）节 点上的能见度。 ４）信息素的更新 当全部蚂蚁从原点出发，１５ 个单位时间过后， 每只蚂蚁都爬到终点，即完成一次参数寻优。 每经 过 １ 个单位时间，节点（ ｃｉ，ｙｊ ） 信息素强度都会改 变，即 τ（ｃｉ，ｙｊ，ｔ ＋ １５） ＝ ρτ（ｃｉ，ｙｊ，ｔ） ＋ Δτ（ｃｉ，ｙｉ） （１０） Δτ（ｃｉ，ｙｊ） ＝ ∑ ｍ ｋ Δτｋ（ｃｉ，ｙｊ） （１１） Δτｋ（ｃｉ，ｙｊ） ＝ Ｑ／ Ｆｋ ０{ （１２） 式中：ρ 为信息素挥发系数；ｍ 为蚂蚁的数量；Ｑ 为 信息素增强系数，由经验取值；Ｆｋ 表示第 ｋ 只蚂蚁 在本次循环中的目标函数值。 ２．３ 仿真及结果分析 用文献［２２］中船舶模型作为控制模型，当分岔 参数 Ｋ ＝ ２ 时的混沌系统转化为式（４）形式的传递 函数为被控函数，采样周期为 １ ｍｓ，输入信号为阶 跃信号。 混沌蚁群优化算法方案选取如下：迭代次数Ｎ＝ ５０，蚂蚁总数 ｍ ＝ ３０，信息素挥发系数 ρ ＝ ０．８５，信息 素增强系数 Ｑ＝ １，蚂蚁爬行速度 ｖ ＝ ０．３，经过 ５０ 次 迭代后，寻到最优控制参数 ＫＰ ＝ １６．５６３，ＫＩ ＝ ２．０１３， ＫＤ ＝ ０．２３７，表 １ 给出了基于混沌蚁群算法的 ＰＩＤ 参 数优化算法与基于遗传算法的 ＰＩＤ 参数优化算法 的优化值比较结果。 表 １ ＰＩＤ 参数优化算法比较 Ｔａｂｌｅ １ Ｃｏｍｐａｒｉｓｏｎ ｏｆ ＰＩＤ ｐａｒａｍｅｔｅｒ ｏｐｔｉｍｉｚａｔｉｏｎ ａｌｇｏｒｉｔｈｍ 迭代 次数 搜索区域 最优值 基于混沌蚁群算法 ５０ ＫＰ∈［０ ５０］ ＫＰ ＝ １６．５６３ ＫＩ∈［０ １０］ ＫＩ ＝ ２．０１３ ＫＤ∈［０ １０］ ＫＤ ＝ ０．２３７ 基于遗传算法 １００ ＫＰ∈［０ ２５］ ＫＰ ＝ １２．５６３ ＫＩ∈［０ １］ ＫＩ ＝ １．８５３ ＫＤ∈［０ １］ ＫＤ ＝ ０．５９７ 由表 １ 可知：选择合理参数后，基于混沌蚁群算 法的 ＰＩＤ 控制参数寻优算法获得的最优解优于基 于遗传算法的 ＰＩＤ 参数优化算法获得的最优解。 图 ７ 为基于遗传算法的 ＰＩＤ 参数优化算法的系 统响应图，图 ８ 为基于混沌蚁群算法的 ＰＩＤ 参数优 化算法的系统响应图。 由图 ７ 和图 ８ 的对比可以看 出，基于混沌蚁群算法的 ＰＩＤ 参数优化算法能够快 速抑制系统混沌现象，在反映时间上，较遗传算法 减少 ５０％以上。 图 ７ 基于遗传算法的 ＰＩＤ 控制系统的响应 Ｆｉｇ．７ Ｒｅｓｐｏｎｓｅｓ ｏｆ ＰＩＤ ｃｏｎｔｒｏｌ ｓｙｓｔｅｍ ｂａｓｅｄ ｏｎ ｇｅｎｅｔｉｃ ａｌｇｏｒｉｔｈｍ 图 ８ 基于混沌蚁群算法的 ＰＩＤ 控制系统的响应 Ｆｉｇ．８ Ｒｅｓｐｏｎｓｅｓ ｏｆ ＰＩＤ ｃｏｎｔｒｏｌ ｓｙｓｔｅｍ ｂａｓｅｄ ｏｎ ｃｈａｏｓ ａｎｔ ｃｏｌｏｎｙ ｏｐｔｉｍｉｚａｔｉｏｎ 为验证算法对船舶综合减摇系统控制的有效 性，分别采用基于混沌蚁群优化算法和遗传优化算 法在不同海情下得到的 ＰＩＤ 控制参数最优值如表 ２ 和表 ３ 所示。 表 ２ 基于混沌蚁群算法的 ＰＩＤ 控制参数最优值 Ｔａｂｌｅ ２ Ｔｈｅ ｏｐｔｉｍａｌ ｖａｌｕｅ ｏｆ ＰＩＤ ｃｏｎｔｒｏｌ ｐａｒａｍｅｔｅｒｓ ｂａｓｅｄ ｏｎ ｃｈａｏｓ ａｎｔ ｃｏｌｏｎｙ ａｌｇｏｒｉｔｈｍ 有义波高／ ｍ 遭遇角／ （°） ＫＰ ＫＩ ＫＤ η ２．５ ４５ ５．９７ １２．３０ ０．４４ ７８．５ ９０ ７．２３ １９．５４ ０．４０ ８７．９ ３．３ ４５ ５．３２ １４．８４ ０．３７ ７５．２ ９０ ６．２６ １８．６３ ０．３０ ８６．６ ·３２２· 智 能 系 统 学 报 第 １２ 卷