
第12卷第3期 智能系统学报 Vol.12 No.3 2017年6月 CAAl Transactions on Intelligent Systems Jun.2017 D0D0I:10.11992/tis.201605029 网络出版地址:http:/kns.cmki.ne/kcms/detail/23.1538.TP.20170705.1656.008.html 粗匹配和局部尺度压缩搜索下的快速ICP-SLAM 张金艺12,梁滨1,唐笛恺,姚维强2,鲍深 (1.上海大学通信与信息工程学院,上海200010:2.上海大学微电子研究与开发中心,上海200010) 摘要:ICP-SLAM在自主机器人和无人驾驶领域得到了极大的关注,但传统ICP.SLAM缺少当前帧和全局地图的相 对位置关系,因此本文ICP算法必须经过大量的迭代之后才能达到收敛条件,这导致传统ICP-SLAM实时性很差。 并且在每一次的迭代过程中,必须通过全局搜索才能完成匹配点搜索,这进一步降低了传统ICP-SLAM的实时性。 为此,提出了一种快速ICP-SLAM方案。首先,通过MEMS磁力计和全局地标计算出初始位姿矩阵,通过该初始位姿 矩阵实现当前帧和全局地图之间粗匹配,进而减少达到收敛条件的迭代次数。其次,在每次迭代过程中,将采用局 部尺度压缩搜索完成匹配点搜索,从而减小ICP-SLAM的计算开销,提高ICP-SLAM实时性:同时,每次迭代完成之 后,还将通过动态阈值缩小搜索范围,达到加快匹配点搜索的速度,进而提高ICP-SLAM实时性。实验结果表明,和 传统ICP.SLAM相比,在理想室内静止场景下,快速ICP-SLAM的迭代次数最高减小了92.34%,ICP算法运行时间最 高降低了98.86%。除此之外,ICP-SLAM的整体负载也被保持在可控范围内,ICP-SLAM的整体性能得到很大的 提升。 关键词:ICP-SLAM;粗匹配;初始姿态矩阵;局部搜索;动态阈值;实时性;点云;迭代: 中图分类号:TP11文献标志码:A文章编号:1673-4785(2017)03-0413-09 中文引用格式:张金艺,梁滨,唐笛恺,等.粗匹配和局部尺度压缩搜索下的快速ICP-SLAM[J].智能系统学报,2017,12(3): 413-421. 英文引用格式:ZHANG Jinyi,LIANG bin,TANG Dikai,etal.Fast ICP-SLAM with rough alignment and local scale-compressed searching[J].CAAI transactions on intelligent systems,2017,12(3):413-421. Fast ICP-SLAM with rough alignment and local scale-compressed searching ZHANG Jinyi'2,LIANG Bin',TANG Dikai',YAO Weiqiang?,BAO Shen2 (1.School of Communication and Information Engineering,Shanghai University,Shanghai 200010,China;2.Microelectronic Research and Development Center,Shanghai University,Shanghai 200010,China) Abstract:ICP-SLAM has received much attention in the field of autonomous robots and unmanned cars.However, two deficiencies in traditional ICP-SLAM usually result in poor real-time performance.The first is the fact that the relative position between the current scan frame and the global map is not previously known.As a result,the ICP algorithm takes a large number of iterations to reach convergence.The second is that the establishment of correspondence is carried out by global searching and this requires an enormous amount of computational time.To overcome these problems,a fast ICP-SLAM is proposed.To decrease the number of iterations a rough alignment, based on an initial pose matrix,is proposed.In detail,the initial pose matrix is computed using a MEMS magnetometer and global landmarks.Then,a rough alignment is applied between the current scan frame and the global map at the beginning of the ICP algorithm with an initial pose matrix.To accelerate the establishment of correspondence,local scale-compressed searching with a dynamic threshold is proposed where match-points are found within a progressively constrictive range.Compared to traditional ICP-SLAM,under ideal stable conditions, the best experimental results show amount of iteration for ICP algorithm to reach convergence reduces 92.34%and ICP algorithm runtime reduces 98.86%.In addition,computational cost is kept at a stable level due to the elimination of accumulated computational consumption.Moreover,great improvement is observed in the quality and robustness of SLAM Keywords:ICP-SLAM;rough alignment;initial pose matrix;local searching;dynamic threshold;real-time performance;cloud point;iteration 自主机器人和无人驾驶车成为近几年来人工智能领域研究的新热点,该技术在服务业、交通运 收稿日期:2016-05-27.网络出版日期:2017-07-05 输、工业、环境勘探、国防以及生活各个方面都有着 基金项目:国家“863”计划基金项目(2013AA03A1121,2013AABA112):上广阔的应用前景。同时德国工业4.0及中国制造 海市教委重点学科资助项目(J50104). 通信作者:梁滨.E-mail:zhangjinyic@staff.shu.cdu.cn 2025也把焦点聚集在无人化和智能化,智能产业正
第 12 卷第 3 期 智 能 系 统 学 报 Vol.12 №.3 2017 年 6 月 CAAI Transactions on Intelligent Systems Jun. 2017 DOIDOI:10.11992 / tis.201605029 网络出版地址:http: / / kns.cnki.net / kcms/ detail / 23.1538.TP.20170705.1656.008.html 粗匹配和局部尺度压缩搜索下的快速 ICP⁃SLAM 张金艺1,2 ,梁滨1 ,唐笛恺1 ,姚维强2 ,鲍深2 (1.上海大学 通信与信息工程学院,上海 200010;2. 上海大学 微电子研究与开发中心,上海 200010) 摘 要:ICP⁃SLAM 在自主机器人和无人驾驶领域得到了极大的关注,但传统 ICP⁃SLAM 缺少当前帧和全局地图的相 对位置关系,因此本文 ICP 算法必须经过大量的迭代之后才能达到收敛条件,这导致传统 ICP⁃SLAM 实时性很差。 并且在每一次的迭代过程中,必须通过全局搜索才能完成匹配点搜索,这进一步降低了传统 ICP⁃SLAM 的实时性。 为此,提出了一种快速 ICP⁃SLAM 方案。 首先,通过 MEMS 磁力计和全局地标计算出初始位姿矩阵,通过该初始位姿 矩阵实现当前帧和全局地图之间粗匹配,进而减少达到收敛条件的迭代次数。 其次,在每次迭代过程中,将采用局 部尺度压缩搜索完成匹配点搜索,从而减小 ICP⁃SLAM 的计算开销,提高 ICP⁃SLAM 实时性;同时,每次迭代完成之 后,还将通过动态阈值缩小搜索范围,达到加快匹配点搜索的速度,进而提高 ICP⁃SLAM 实时性。 实验结果表明,和 传统 ICP⁃SLAM 相比,在理想室内静止场景下,快速 ICP⁃SLAM 的迭代次数最高减小了 92.34%,ICP 算法运行时间最 高降低了 98.86%。 除此之外,ICP⁃SLAM 的整体负载也被保持在可控范围内,ICP⁃SLAM 的整体性能得到很大的 提升。 关键词:ICP⁃SLAM;粗匹配;初始姿态矩阵;局部搜索;动态阈值;实时性;点云;迭代; 中图分类号: TP11 文献标志码:A 文章编号:1673-4785(2017)03-0413-09 中文引用格式:张金艺,梁滨,唐笛恺,等. 粗匹配和局部尺度压缩搜索下的快速 ICP-SLAM[ J]. 智能系统学报, 2017, 12( 3): 413-421. 英文引用格式:ZHANG Jinyi, LIANG bin,TANG Dikai,et al. Fast ICP⁃SLAM with rough alignment and local scale⁃compressed searching[J]. CAAI transactions on intelligent systems, 2017, 12(3): 413-421. Fast ICP⁃SLAM with rough alignment and local scale⁃compressed searching ZHANG Jinyi 1,2 , LIANG Bin 1 ,TANG Dikai 1 ,YAO Weiqiang 2 ,BAO Shen 2 (1.School of Communication and Information Engineering, Shanghai University, Shanghai 200010, China; 2. Microelectronic Research and Development Center, Shanghai University, Shanghai 200010, China) Abstract:ICP⁃SLAM has received much attention in the field of autonomous robots and unmanned cars. However, two deficiencies in traditional ICP⁃SLAM usually result in poor real⁃time performance. The first is the fact that the relative position between the current scan frame and the global map is not previously known. As a result, the ICP algorithm takes a large number of iterations to reach convergence. The second is that the establishment of correspondence is carried out by global searching and this requires an enormous amount of computational time. To overcome these problems, a fast ICP⁃SLAM is proposed. To decrease the number of iterations a rough alignment, based on an initial pose matrix, is proposed. In detail, the initial pose matrix is computed using a MEMS magnetometer and global landmarks. Then, a rough alignment is applied between the current scan frame and the global map at the beginning of the ICP algorithm with an initial pose matrix. To accelerate the establishment of correspondence, local scale⁃compressed searching with a dynamic threshold is proposed where match⁃points are found within a progressively constrictive range.Compared to traditional ICP⁃SLAM, under ideal stable conditions, the best experimental results show amount of iteration for ICP algorithm to reach convergence reduces 92.34% and ICP algorithm runtime reduces 98. 86%. In addition, computational cost is kept at a stable level due to the elimination of accumulated computational consumption. Moreover, great improvement is observed in the quality and robustness of SLAM Keywords: ICP⁃SLAM; rough alignment; initial pose matrix; local searching; dynamic threshold; real⁃time performance; cloud point; iteration 收稿日期:2016-05-27. 网络出版日期:2017-07-05. 基金项目:国家“863”计划基金项目(2013AA03A1121,2013AA03A1122);上 海市教委重点学科资助项目(J50104). 通信作者:梁滨.E⁃mail: zhangjinyi@ staff.shu.edu.cn. 自主机器人和无人驾驶车成为近几年来人工 智能领域研究的新热点,该技术在服务业、交通运 输、工业、环境勘探、国防以及生活各个方面都有着 广阔的应用前景。 同时德国工业 4. 0 及中国制造 2025 也把焦点聚集在无人化和智能化,智能产业正

·414 智能系统学报 第12卷 在迎来前所未有的发展机遇,将催生庞大的市场。 Matching Rule方法[u。该方法通过在极坐标系下, SLAM(同时定位和地图创建,simultaneous 寻找相近的旋转角度,实现了快速的匹配点搜索。 localization and mapping,)是自主机器人和无人驾驶 但该方法并不能提供初始姿态矩阵实现粗匹配,所 车领域的关键技术。当前SLAM的实现方案可以分 以仍然采用全局搜索实现匹配点搜索。综上,可以 为基于概率的方案1-]和基于非概率的方案[4)。 看出大多数ICP算法都采用了全局搜索。但随着全 ICP(最近邻点迭代,iterative closest point)-SLAM作 局地图的扩大,全局搜索会导致计算消耗量的累计 为基于非概率的方案之一,由于其具有原理简单、 效应。虽然局部ICP-SLAM20-2某种程度上可以解 成本较低等优点而得到了广泛关注[6】。并且相比 决这个问题,但是局部ICP-SLAM首先把全局地图 于传统的导航技术,如蓝牙定位、惯性导航系统 划分成多个局部地图,然后对每个局部地图进行局 等[9-,ICP-SLAM不仅能实现定位,还能实现地图 部ICP-SLAM。所以,局部ICP-SLAM的本质上还是 创建。但随着自主机器人和无人驾驶车的速度越 采用了全局搜索。并且局部ICP-SLAM还要保存各 来越快,所处环境变得越来越复杂,这对SLAM实时 个局部地图的相对位置,增加了额外内存开销。 性提出了更高要求。由于传统ICP-SLAM实时性 综上所述,为了有效提高ICP-SLAM的实时性, 差,同时建模精度和鲁棒性也不高,显然不能再满 本文提出基于粗匹配和局部尺度压缩搜索的快速 足这方面的要求。造成传统ICP-SLAM实时性差的 ICP-SLAM。该快速ICP-SLAM在激光雷达的基础 原因:一方面,因为传统ICP算法不能提供初始姿态 上增加了MEMS磁力计,这个MEMS磁力计能直接 矩阵进行粗匹配,从而导致达到收敛条件的迭代次 输出当前航向角。并且引入全局地标,通过激光雷 数大量增加:另一方面,由于缺少粗匹配,必须通过 达扫描并测量全局地标,计算出机器人当前的位置 全局搜索才能完成匹配点搜索,这也大大增加了计 信息。最后由航向角和机器人当前的位置信息共 算开销,降低了传统ICP-SLAM实时性。因此,为了 同构成完整的初值姿态矩阵。当得到了初值姿态 提高ICP-SLAM的实时性,必须对传统ICP-SLAM 矩阵后,首先通过该初值姿态矩阵实现当前帧和全 进行优化。 局地图的粗匹配。其次,在ICP算法的每次迭代中, 当前,对传统ICP-SLAM的优化大都是选取 采用局部尺度压缩搜索完成匹配点搜索,从而避免 ICP算法的某个步骤进行优化。ICP算法最早由 了由全局搜索带来的巨大计算开销。同时,每次迭 Besl和Mckay为解决3-D物体对准问题而提出 代完成之后,匹配点的搜索范围通过动态阈值被缩 的。根据Rusinkiewicz和Levoy的理论[a)],ICP 小,加快匹配点搜索的速度,这将进一步提高ICP 算法可以分成下面6个步骤:选择控制点,匹配点搜 SLAM实时性。实验结果显示,本文提出的快速 索,计算匹配点权重,设定一个匹配点误差方程,通 ICP-SLAM相比于传统ICP-SLAM,迭代次数减少了 过最小化匹配点误差方程求出旋转矩阵和平移矩 92.34%,ICP算法运行时间减少了98.86%。同时, 阵,同时定位和地图创建。当前ICP算法的研究主 ICP-SLAM的系统负载也被控制在稳定状态,其整 要集中在优化匹配点搜索策略上。主流的匹配点 体性能得到较大的改善。 搜索策略可以大致分为下面几种。基于特征的匹 1 基于初始位姿矩阵的粗匹配 配,点搜索方法[14-6]包括如基于直线特征、基于曲率 特征和基于斜率特征等,该方法在提取几何特征时 从上述分析可以看出,粗匹配是实现快速ICP 增加了额外的计算开销,降低了ICP-SLAM实时性。 SLAM的首要步骤。粗匹配的过程为:通过旋转和 并且几何特征的提取容易受测量噪声和移动物体 平移变换,使得两个形状类似但处于不同空间位置 的影响,降低了ICP-SLAM的鲁棒性。另外,基于几 的物体大致重合。这是因为,当形状相同的两个物 何划分的匹配点搜索也被广泛引用,如Delaunay划 体处于二维平面的不同位置时,必然能找到一个平 分)和K-D树划分)。几何划分可以提高匹配,点 移矩阵和旋转角使得这两个物体完全重合。而机 搜索的质量和效率。但当相邻两帧的重叠区域很 器人的初始位姿矩阵就包含了这样一个平移矩阵 小时,该方法则不再适用。除此之外,考虑到激光 和旋转角。其中,机器人当前的坐标(x,y,)可以看 雷达作为ICP-SLAM的主要传感器,所以为了能更 作平移矩阵,机器人的航向角0,可以看作旋转角。 好地利用激光雷达特殊的数据结构,提出了基于 那么机器人t时刻的姿态矩阵可以表示成一个1×3 Polar-Cartesian Hybrid Transforms Polar Point 矩阵Pose,(x,y,0,)。Pose,(x,y,0,)可以通过
在迎来前所未有的发展机遇,将催生庞大的市场。 SLAM ( 同 时 定 位 和 地 图 创 建, simultaneous localization and mapping,)是自主机器人和无人驾驶 车领域的关键技术。 当前 SLAM 的实现方案可以分 为基于概率的方案[1-3] 和基于非概率的方案[4-5] 。 ICP(最近邻点迭代,iterative closest point)⁃SLAM 作 为基于非概率的方案之一,由于其具有原理简单、 成本较低等优点而得到了广泛关注[6-8] 。 并且相比 于传统的导航技术, 如蓝牙定位、 惯性导航系统 等[9-11] ,ICP⁃SLAM 不仅能实现定位,还能实现地图 创建。 但随着自主机器人和无人驾驶车的速度越 来越快,所处环境变得越来越复杂,这对 SLAM 实时 性提出了更高要求。 由于传统 ICP⁃SLAM 实时性 差,同时建模精度和鲁棒性也不高,显然不能再满 足这方面的要求。 造成传统 ICP⁃SLAM 实时性差的 原因:一方面,因为传统 ICP 算法不能提供初始姿态 矩阵进行粗匹配,从而导致达到收敛条件的迭代次 数大量增加;另一方面,由于缺少粗匹配,必须通过 全局搜索才能完成匹配点搜索,这也大大增加了计 算开销,降低了传统 ICP⁃SLAM 实时性。 因此,为了 提高 ICP⁃SLAM 的实时性,必须对传统 ICP⁃SLAM 进行优化。 当前,对传统 ICP - SLAM 的优化大都是选取 ICP 算法的某个步骤进行优化。 ICP 算法最早由 Besl 和 Mckay 为解决 3⁃D 物体对准问题而提出 的[12] 。 根据 Rusinkiewicz 和 Levoy 的理论[13] ,ICP 算法可以分成下面 6 个步骤:选择控制点,匹配点搜 索,计算匹配点权重,设定一个匹配点误差方程,通 过最小化匹配点误差方程求出旋转矩阵和平移矩 阵,同时定位和地图创建。 当前 ICP 算法的研究主 要集中在优化匹配点搜索策略上。 主流的匹配点 搜索策略可以大致分为下面几种。 基于特征的匹 配点搜索方法[14-16]包括如基于直线特征、基于曲率 特征和基于斜率特征等,该方法在提取几何特征时 增加了额外的计算开销,降低了 ICP⁃SLAM 实时性。 并且几何特征的提取容易受测量噪声和移动物体 的影响,降低了 ICP⁃SLAM 的鲁棒性。 另外,基于几 何划分的匹配点搜索也被广泛引用,如 Delaunay 划 分[17]和 K⁃D 树划分[18] 。 几何划分可以提高匹配点 搜索的质量和效率。 但当相邻两帧的重叠区域很 小时,该方法则不再适用。 除此之外,考虑到激光 雷达作为 ICP⁃SLAM 的主要传感器,所以为了能更 好地利用激光雷达特殊的数据结构,提出了基于 Polar⁃Cartesian Hybrid Transforms 的 Polar Point Matching Rule 方法[19] 。 该方法通过在极坐标系下, 寻找相近的旋转角度,实现了快速的匹配点搜索。 但该方法并不能提供初始姿态矩阵实现粗匹配,所 以仍然采用全局搜索实现匹配点搜索。 综上,可以 看出大多数 ICP 算法都采用了全局搜索。 但随着全 局地图的扩大,全局搜索会导致计算消耗量的累计 效应。 虽然局部 ICP⁃SLAM [20-21]某种程度上可以解 决这个问题,但是局部 ICP⁃SLAM 首先把全局地图 划分成多个局部地图,然后对每个局部地图进行局 部 ICP⁃SLAM。 所以,局部 ICP⁃SLAM 的本质上还是 采用了全局搜索。 并且局部 ICP⁃SLAM 还要保存各 个局部地图的相对位置,增加了额外内存开销。 综上所述,为了有效提高 ICP⁃SLAM 的实时性, 本文提出基于粗匹配和局部尺度压缩搜索的快速 ICP⁃SLAM。 该快速 ICP⁃SLAM 在激光雷达的基础 上增加了 MEMS 磁力计,这个 MEMS 磁力计能直接 输出当前航向角。 并且引入全局地标,通过激光雷 达扫描并测量全局地标,计算出机器人当前的位置 信息。 最后由航向角和机器人当前的位置信息共 同构成完整的初值姿态矩阵。 当得到了初值姿态 矩阵后,首先通过该初值姿态矩阵实现当前帧和全 局地图的粗匹配。 其次,在 ICP 算法的每次迭代中, 采用局部尺度压缩搜索完成匹配点搜索,从而避免 了由全局搜索带来的巨大计算开销。 同时,每次迭 代完成之后,匹配点的搜索范围通过动态阈值被缩 小,加快匹配点搜索的速度,这将进一步提高 ICP⁃ SLAM 实时性。 实验结果显示,本文提出的快速 ICP⁃SLAM 相比于传统 ICP⁃SLAM,迭代次数减少了 92.34%,ICP 算法运行时间减少了 98.86%。 同时, ICP⁃SLAM 的系统负载也被控制在稳定状态,其整 体性能得到较大的改善。 1 基于初始位姿矩阵的粗匹配 从上述分析可以看出,粗匹配是实现快速 ICP⁃ SLAM 的首要步骤。 粗匹配的过程为:通过旋转和 平移变换,使得两个形状类似但处于不同空间位置 的物体大致重合。 这是因为,当形状相同的两个物 体处于二维平面的不同位置时,必然能找到一个平 移矩阵和旋转角使得这两个物体完全重合。 而机 器人的初始位姿矩阵就包含了这样一个平移矩阵 和旋转角。 其中,机器人当前的坐标(xt,yt)可以看 作平移矩阵,机器人的航向角 θt 可以看作旋转角。 那么机器人 t 时刻的姿态矩阵可以表示成一个 1×3 矩阵 Poset ( xt, yt,θt )。 Poset ( xt, yt, θt ) 可以通过 ·414· 智 能 系 统 学 报 第 12 卷

第3期 张金艺,等:粗匹配和局部尺度压缩搜索下的快速ICP-SLAM ·415 MEMS磁力计和全局地标计算得到。这样在ICP算 虚线),结合式(5),则F,可以通过式(6)得到,其中 法开始前,可以通过矩阵Pose,(x,y,0,)完成当前 F,'和F,都是一个N×2矩阵,如式(7)和式(8) 帧和全局地图的粗匹配。全局地标在全局坐标系 所示: 中的坐标为已知信息,设图1中的第n个全局地标 cos 0. sin 0, 在全局坐标系中的坐标为Pn-c(xa-c,yLa-c)。同时 (5) sin 0.cos 6. 设第n个全局地标在机器人局部坐标系的坐标为 「x,y: P-(x1,y-L),则(x,y,)可以通过式(1)计算 x y 得到: F =F'Trolate (6) (x:xin-c xLn-Lcos 0:yi-Lsin 0 (1) y:=yin-c xu-Lsin 0:-yi-Lcos0. AY x2 y2 △全局地标nPL(代na) F= (7) Pind(xiG YiG) XN yN x y1 人全局地标1 X2 y2 F,= (8) XN yN Puu yu 通过粗匹配后,ICP算法达到收敛条件的迭代 Pud(xug yuG 次数将会大大减小。最后,当ICP算法达到收敛条 0 件时,得到最终的变换矩阵T,(x,,y,0)。 图1计算姿态矩阵 P(x.v.0) Fig.1 Initial pose matrix 当机器人移动到图2中的(x,y,)位置时,设其 姿态矩阵为Pose,(x,y,0)。激光雷达获取当前扫 描帧并记为F,'(图2中的灰色圆部分),并测出第n 个全局地标在机器人局部坐标系下的坐标P (x-Ly-L)。假设激光雷达的角度分辨率为p,则 F'中的点数N可通过式(2)得到 N=o/p (2) 式中p为激光雷达的可视角(例如360°)。根据 图2粗匹配示意图 (1)式可计算出(x,y),如式(3)所示: Fig.2 Rough align TPun-L Pin-c (3) y 2基于动态阈值的局部尺度压缩搜索 式中T如公式(4)所示: 粗匹配完成之后,当前帧中的点和其匹配点的 -c0s0, sin 0, 距离被大大缩小,所以本文中的匹配点搜索将通过 T= (4) sin 0, cos 0, 局部搜索完成。同时,每次迭代完成之后,匹配点 因为全局地标为全局的静态参照物,所以通过 之间的距离都比上一次迭代时更小,此时便可以通 该方法计算得到的Pose,(x,y,0,)不存在累计 过动态阈值达到尺度压缩,从而缩小匹配,点搜索的 误差。 范围。局部尺度压缩搜索不仅能加快匹配点搜索 同样在图2中记全局地图为Mh(图2中的点 速度,还能提高匹配点搜索质量。同时在本文中, 线),并记F,'和M粗匹配的结果为F(图2中的 因为SLAM创建的地图为栅格地图,所以本小节将
MEMS 磁力计和全局地标计算得到。 这样在 ICP 算 法开始前,可以通过矩阵 Poset( xt,yt,θt )完成当前 帧和全局地图的粗匹配。 全局地标在全局坐标系 中的坐标为已知信息,设图 1 中的第 n 个全局地标 在全局坐标系中的坐标为 PLn-G( xLn-G ,yLn-G )。 同时 设第 n 个全局地标在机器人局部坐标系的坐标为 PLn-L(xLn-L ,yLn-L ),则( xt,yt ) 可以通过式( 1) 计算 得到: xt = xLn-G - xLn-L cos θt - yLn-L sin θt yt = yLn-G + xLn-L sin θt - yLn-L cosθt { (1) 图 1 计算姿态矩阵 Fig.1 Initial pose matrix 当机器人移动到图 2 中的(xt,yt)位置时,设其 姿态矩阵为 Poset(xt,yt,θt)。 激光雷达获取当前扫 描帧并记为 Ft ′(图 2 中的灰色圆部分),并测出第 n 个全局地标在机器人局部坐标系下的坐标 PLn-L (xLn-L ,yLn-L )。 假设激光雷达的角度分辨率为 ρ,则 Ft ′中的点数 N 可通过式(2)得到 N = φ/ ρ (2) 式中 φ 为激光雷达的可视角( 例如 360°)。 根据 (1)式可计算出(xt,yt),如式(3)所示: xt yt é ë ê ê ù û ú ú = TPLn-L + PLn-G (3) 式中 T 如公式(4)所示: T = - cos θt - sin θt sin θt - cos θt é ë ê ê ù û ú ú (4) 因为全局地标为全局的静态参照物,所以通过 该方法计算得到的 Poset ( xt, yt, θt ) 不存在累计 误差。 同样在图 2 中记全局地图为Mglobal(图 2 中的点 线),并记 Ft ′和 Mglobal粗匹配的结果为 Ft(图 2 中的 虚线),结合式(5),则 Ft 可以通过式(6)得到,其中 Ft ′和 Ft 都是一个 N × 2 矩阵,如式( 7) 和式( 8) 所示: Trotate = cos θt sin θt - sin θt cos θt é ë ê ê ù û ú ú (5) Ft = Ft ′Trotate + xt yt xt yt ︙ ︙ xt yt é ë ê ê ê ê ê ê ù û ú ú ú ú ú ú N×2 (6) Ft ′ = x1 ′ y1 ′ x2 ′ y2 ′ ︙ ︙ xN ′ yN ′ é ë ê ê ê ê ê ê ù û ú ú ú ú ú ú (7) Ft = x1 y1 x2 y2 ︙ ︙ xN yN é ë ê ê ê ê ê ê ù û ú ú ú ú ú ú (8) 通过粗匹配后,ICP 算法达到收敛条件的迭代 次数将会大大减小。 最后,当 ICP 算法达到收敛条 件时,得到最终的变换矩阵 Tt x T t ,y T t ,θ T t ( ) 。 图 2 粗匹配示意图 Fig.2 Rough align 2 基于动态阈值的局部尺度压缩搜索 粗匹配完成之后,当前帧中的点和其匹配点的 距离被大大缩小,所以本文中的匹配点搜索将通过 局部搜索完成。 同时,每次迭代完成之后,匹配点 之间的距离都比上一次迭代时更小,此时便可以通 过动态阈值达到尺度压缩,从而缩小匹配点搜索的 范围。 局部尺度压缩搜索不仅能加快匹配点搜索 速度,还能提高匹配点搜索质量。 同时在本文中, 因为 SLAM 创建的地图为栅格地图,所以本小节将 第 3 期 张金艺,等:粗匹配和局部尺度压缩搜索下的快速 ICP-SLAM ·415·
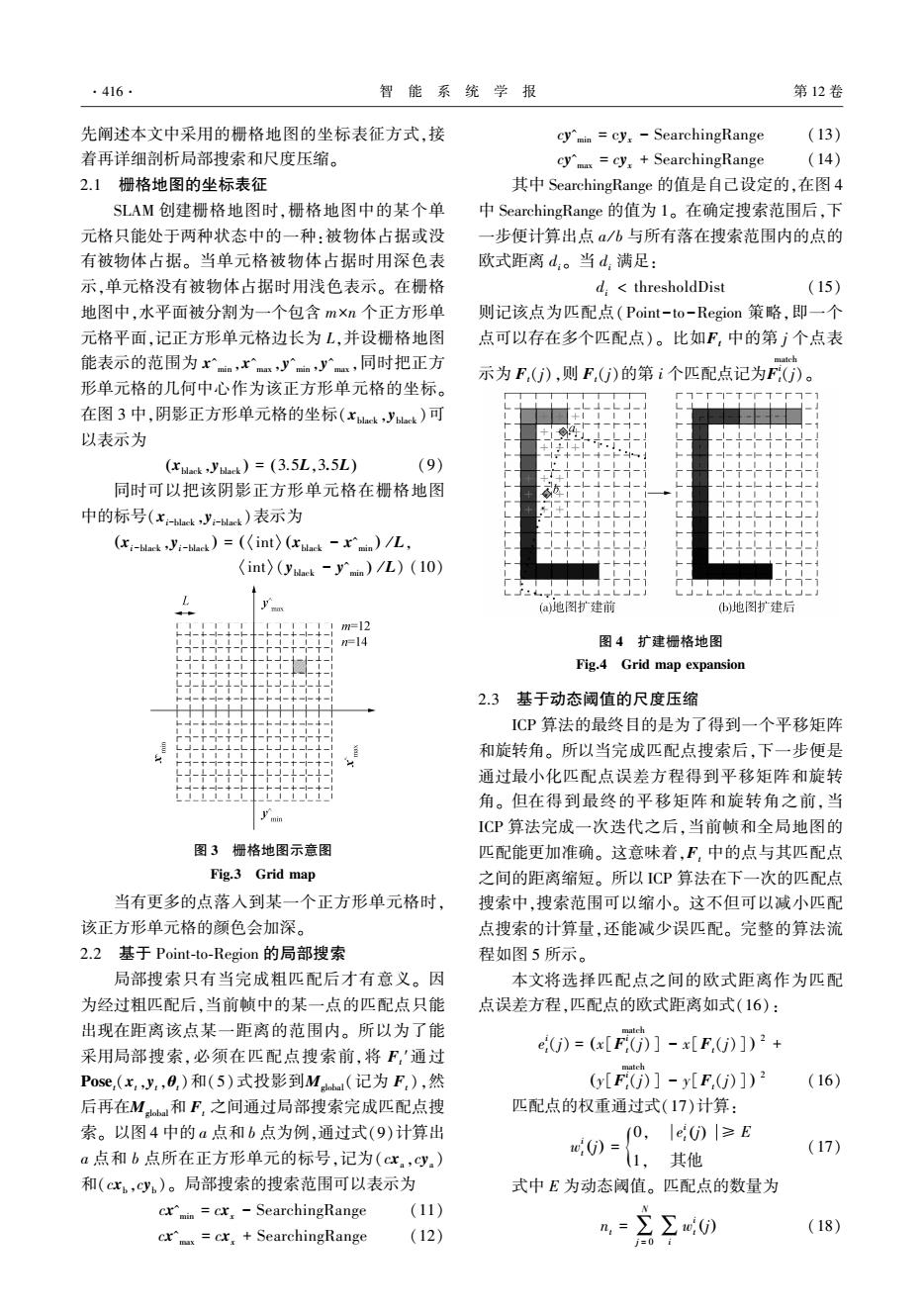
·416 智能系统学报 第12卷 先阐述本文中采用的栅格地图的坐标表征方式,接 cy"min cy,-SearchingRange (13) 着再详细剖析局部搜索和尺度压缩。 cy"max cy,SearchingRange (14) 2.1栅格地图的坐标表征 其中SearchingRange的值是自己设定的,在图4 SLAM创建栅格地图时,栅格地图中的某个单 中SearchingRange的值为l。在确定搜索范围后,下 元格只能处于两种状态中的一种:被物体占据或没 一步便计算出点a/b与所有落在搜索范围内的点的 有被物体占据。当单元格被物体占据时用深色表 欧式距离d。当d,满足: 示,单元格没有被物体占据时用浅色表示。在栅格 d<thresholdDist (15) 地图中,水平面被分割为一个包含m×n个正方形单 则记该点为匹配点(Point--to-Region策略,即一个 元格平面,记正方形单元格边长为L,并设栅格地图 点可以存在多个匹配点)。比如F,中的第广个点表 能表示的范围为xnxy。y,同时把正方 示为F,(),则F,(G)的第i个匹配点记为F(j)。 形单元格的几何中心作为该正方形单元格的坐标。 在图3中,阴影正方形单元格的坐标(xu4,Jyt)可 以表示为 (black y plack)=(3.5L,3.5L) (9) 同时可以把该阴影正方形单元格在栅格地图 中的标号(xty-hd)表示为 (x-blacky:-het)=(int)(xuat-xn)/L, (int)(yuek -y)/L)(10) L (a地图扩建前 b)地图扩建后 L1m=12 n=14 图4扩建栅格地图 Fig.4 Grid map expansion 2.3基于动态阈值的尺度压缩 ICP算法的最终目的是为了得到一个平移矩阵 和旋转角。所以当完成匹配,点搜索后,下一步便是 +- -- 通过最小化匹配点误差方程得到平移矩阵和旋转 角。但在得到最终的平移矩阵和旋转角之前,当 y'nn ICP算法完成一次迭代之后,当前帧和全局地图的 图3栅格地图示意图 匹配能更加准确。这意味着,F,中的点与其匹配点 Fig.3 Grid map 之间的距离缩短。所以ICP算法在下一次的匹配点 当有更多的点落入到某一个正方形单元格时, 搜索中,搜索范围可以缩小。这不但可以减小匹配 该正方形单元格的颜色会加深。 点搜索的计算量,还能减少误匹配。完整的算法流 2.2基于Point-to-Region的局部搜索 程如图5所示。 局部搜索只有当完成粗匹配后才有意义。因 本文将选择匹配点之间的欧式距离作为匹配 为经过粗匹配后,当前帧中的某一点的匹配点只能 点误差方程,匹配点的欧式距离如式(16): 出现在距离该点某一距离的范围内。所以为了能 )=[F]-x[E,0)])2+ 采用局部搜索,必须在匹配点搜索前,将F'通过 Pose,(x,y,0,)和(5)式投影到Ma(记为F,),然 6[F1-[F.0)1) (16) 后再在M和F,之间通过局部搜索完成匹配,点搜 匹配点的权重通过式(17)计算: 索。以图4中的a点和b点为例,通过式(9)计算出 (0, Ie0)|≥E a点和b点所在正方形单元的标号,记为(cx,cy.) 0=1. (17) 其他 和(cx。,cy)。局部搜索的搜索范围可以表示为 式中E为动态阈值。匹配点的数量为 cxmin =cx,-SearchingRange (11) -Az0 (18) cx"max =cx,SearchingRange (12)
先阐述本文中采用的栅格地图的坐标表征方式,接 着再详细剖析局部搜索和尺度压缩。 2.1 栅格地图的坐标表征 SLAM 创建栅格地图时,栅格地图中的某个单 元格只能处于两种状态中的一种:被物体占据或没 有被物体占据。 当单元格被物体占据时用深色表 示,单元格没有被物体占据时用浅色表示。 在栅格 地图中,水平面被分割为一个包含 m×n 个正方形单 元格平面,记正方形单元格边长为 L,并设栅格地图 能表示的范围为 x^min ,x^max,y^min ,y^max,同时把正方 形单元格的几何中心作为该正方形单元格的坐标。 在图 3 中,阴影正方形单元格的坐标(xblack ,yblack )可 以表示为 xblack ,yblack ( ) = (3.5L,3.5L) (9) 同时可以把该阴影正方形单元格在栅格地图 中的标号(xi-black ,yi-black )表示为 xi-black ,yi-black ( ) = 〈int〉 xblack - x^min ( ( ) / L, 〈int〉(yblack - y^min ) / L) (10) 图 3 栅格地图示意图 Fig.3 Grid map 当有更多的点落入到某一个正方形单元格时, 该正方形单元格的颜色会加深。 2.2 基于 Point⁃to⁃Region 的局部搜索 局部搜索只有当完成粗匹配后才有意义。 因 为经过粗匹配后,当前帧中的某一点的匹配点只能 出现在距离该点某一距离的范围内。 所以为了能 采用局部搜索,必须在匹配点搜索前,将 Ft ′通过 Poset(xt,yt,θt)和(5)式投影到Mglobal(记为 Ft),然 后再在Mglobal和 Ft 之间通过局部搜索完成匹配点搜 索。 以图 4 中的 a 点和 b 点为例,通过式(9)计算出 a 点和 b 点所在正方形单元的标号,记为(cxa,cya) 和(cxb ,cyb )。 局部搜索的搜索范围可以表示为 cx^min = cxx - SearchingRange (11) cx^max = cxx + SearchingRange (12) cy^min = cyx - SearchingRange (13) cy^max = cyx + SearchingRange (14) 其中 SearchingRange 的值是自己设定的,在图 4 中 SearchingRange 的值为 1。 在确定搜索范围后,下 一步便计算出点 a / b 与所有落在搜索范围内的点的 欧式距离 di。 当 di 满足: di < thresholdDist (15) 则记该点为匹配点(Point-to-Region 策略,即一个 点可以存在多个匹配点)。 比如Ft 中的第 j 个点表 示为 Ft(j),则 Ft(j)的第 i 个匹配点记为F i t(j) match 。 图 4 扩建栅格地图 Fig.4 Grid map expansion 2.3 基于动态阈值的尺度压缩 ICP 算法的最终目的是为了得到一个平移矩阵 和旋转角。 所以当完成匹配点搜索后,下一步便是 通过最小化匹配点误差方程得到平移矩阵和旋转 角。 但在得到最终的平移矩阵和旋转角之前,当 ICP 算法完成一次迭代之后,当前帧和全局地图的 匹配能更加准确。 这意味着,Ft 中的点与其匹配点 之间的距离缩短。 所以 ICP 算法在下一次的匹配点 搜索中,搜索范围可以缩小。 这不但可以减小匹配 点搜索的计算量,还能减少误匹配。 完整的算法流 程如图 5 所示。 本文将选择匹配点之间的欧式距离作为匹配 点误差方程,匹配点的欧式距离如式(16): e i t(j) = x[F i t(j) match ( ] - x[Ft(j)] ) 2 + y[F i t(j) match ( ] - y[Ft(j)] ) 2 (16) 匹配点的权重通过式(17)计算: w i t (j) = 0, e i t (j) ≥ E {1, 其他 (17) 式中 E 为动态阈值。 匹配点的数量为 nt = ∑ N j = 0 ∑i w i t (j) (18) ·416· 智 能 系 统 学 报 第 12 卷

第3期 张金艺,等:粗匹配和局部尺度压缩搜索下的快速ICP-SLAM ·417. 开始 al, =0→yc (22) 扫描得到F,计算出P,化,y) ay, al, 将F转换为F, =0→0m (23) a0. 通过局部尺度压缩搜索完成配点搜索 完成一次迭代之后,E通过下式被缩小: E=EFe,Fe∈(0,l) (24) ICP算法迭代 人 当L,达到阈值后,ICP算法停止并得到最终的 是否达到收敛条件 N E-EFa 变换矩阵T,(x,y,O)。F,通过该变换矩阵转换成 Y F(图4中的虚线),并最终实现Mm的扩建。 得到T,男) F+1 3实验结果与分析 LAM院成N 为了有效验证粗匹配和局部尺度压缩搜索对 结束 ICP-SLAM实时性的改善,本文搭建了一辆可定位 图5算法总流程图 的小车作为验证平台。该小车搭载了一个 Fig.5 Algorithm flow chart RobotPeak激光雷达、一个Uranus MEMS磁力计和 当前帧与全局地图的重合度可以表示为 一块Raspberry Pi主板,如图6所示,各传感器规格 n. 见表1。 0,=N*1 (19) 综上,最终的误差方程可以表示为 ΣG0601 Raspberry Pi I,= j=0 (20) n,OL RobotPeak激光雷达 通过求导可以完成(20)式的最小化,得出变换 矩阵(x",y",): al, Uranus MEMS磁力计 =0→x (21) ox, 图6实验平台 Fig.6 Experiment platform 表1 RobotPeak激光雷达和Uranus MEMS磁力计参数 Table 1 Features of Robot Peak and Uranus MEMS 传感器 测量范围 采样频率/Hz 距离分辨率/cm角度分辨率/(o)FOV(Field of View)/(o) RobotPeak激光雷达 6m 2000 0.2 1 360 Uranus MEMS磁力计 ±4800uT 100 0.01 本小节将从两方面验证快速ICP-SLAM。第 ICP-SLAM实时性的改善情况,同时还可以验证 一方面是快速ICP-SLAM实时性改善验证。首先, ICP-SLAM在建模精度、鲁棒性和计算开销等方面 对比未进行粗匹配和进行粗匹配下ICP-SLAM的 的提升。 迭代次数和ICP算法运行时间,验证粗匹配对 3.1 快速ICP-SLAM实时性改善验证 ICP-SLAM实时性的改善;其次,记录F的值从1 通过第1节和第2节的分析可知,ICP-SLAM实 到O.3变化过程中ICP-SLAM的迭代次数和ICP 时性受初始姿态矩阵、局部搜素和参数F影响。 算法运行时间,观察其变化趋势,进而验证局部尺 本小节将采用复合开环航迹和复合闭环航迹,验证 度压缩搜索对ICP-SLAM实时性的改善。第二方 粗匹配和局部尺度压缩搜索对ICP-SLAM实时性的 面是快速ICP-SLAM整体性改善验证。其不仅可 改善。复合开环航迹和复合闭环航迹分别如图7中 以验证同时采用粗匹配和局部尺度压缩搜索时, 的(a)和(b)所示
图 5 算法总流程图 Fig.5 Algorithm flow chart 当前帧与全局地图的重合度可以表示为 OLt = nt N + 1 (19) 综上,最终的误差方程可以表示为 It = ∑ N j = 0 ∑i w i t (j) e i t [ (j) ] ntOLt (20) 通过求导可以完成(20)式的最小化,得出变换 矩阵 x new t ,y new t ,θ new t ( ) : ∂It ∂xt = 0⇒x new t (21) ∂It ∂yt = 0⇒y new t (22) ∂It ∂θt = 0⇒θ new t (23) 完成一次迭代之后,E 通过下式被缩小: E = EFdec, Fdec ∈ (0,1) (24) 当 It 达到阈值后,ICP 算法停止并得到最终的 变换矩阵Tt x T t ,y T t ,θ T t ( ) 。 Ft 通过该变换矩阵转换成 F c t(图 4 中的虚线),并最终实现Mglobal的扩建。 3 实验结果与分析 为了有效验证粗匹配和局部尺度压缩搜索对 ICP-SLAM 实时性的改善,本文搭建了一辆可定位 的小 车 作 为 验 证 平 台。 该 小 车 搭 载 了 一 个 RobotPeak 激光雷达、一个 Uranus MEMS 磁力计和 一块 Raspberry Pi 主板,如图 6 所示,各传感器规格 见表 1。 图 6 实验平台 Fig.6 Experiment platform 表 1 RobotPeak 激光雷达和 Uranus MEMS 磁力计参数 Table 1 Features of Robot Peak and Uranus MEMS 传感器 测量范围 采样频率/ Hz 距离分辨率/ cm 角度分辨率/ (°) FOV(Field of View) / (°) RobotPeak 激光雷达 6 m 2 000 0.2 1 360 Uranus MEMS 磁力计 ±4 800 μT 100 — 0.01° — 本小节将从两方面验证快速 ICP⁃SLAM。 第 一方面是快速 ICP⁃SLAM 实时性改善验证。 首先, 对比未进行粗匹配和进行粗匹配下 ICP⁃SLAM 的 迭代次 数 和 ICP 算 法 运 行 时 间,验 证 粗 匹 配 对 ICP⁃SLAM 实时性的改善;其次,记录 Fdec的值从 1 到 0.3 变化过程中 ICP⁃SLAM 的迭代次数和 ICP 算法运行时间,观察其变化趋势,进而验证局部尺 度压缩搜索对 ICP⁃SLAM 实时性的改善。 第二方 面是快速 ICP⁃SLAM 整体性改善验证。 其不仅可 以验证同时采用粗匹配和局部尺度压缩搜索时, ICP⁃SLAM 实时性的改善情况,同时还可以验证 ICP⁃SLAM 在建模精度、鲁棒性和计算开销等方面 的提升。 3.1 快速 ICP⁃SLAM 实时性改善验证 通过第 1 节和第 2 节的分析可知,ICP⁃SLAM 实 时性受初始姿态矩阵、局部搜素和参数 Fdec 影响。 本小节将采用复合开环航迹和复合闭环航迹,验证 粗匹配和局部尺度压缩搜索对 ICP⁃SLAM 实时性的 改善。 复合开环航迹和复合闭环航迹分别如图 7 中 的(a)和(b)所示。 第 3 期 张金艺,等:粗匹配和局部尺度压缩搜索下的快速 ICP-SLAM ·417·