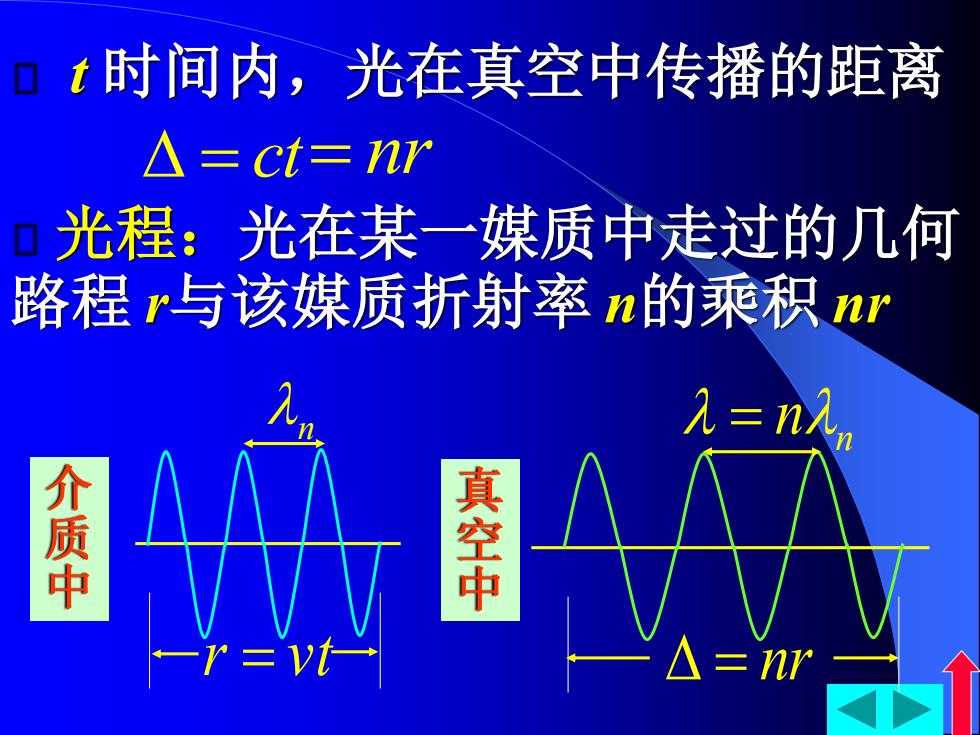
口t时间内,光在真空中传播的距离 △=ct=nr 口光程:光在某一媒质中走过的几何 路程r与该媒质折射率n的乘积nr 2=n2, 介质中 真空中 =nr
= ct t 时间内,光在真空中传播的距离 = nr 光程:光在某一媒质中走过的几何 路程 r与该媒质折射率 n的乘积 nr r = vt = nr 介 质 中 真 空 中 n n = n
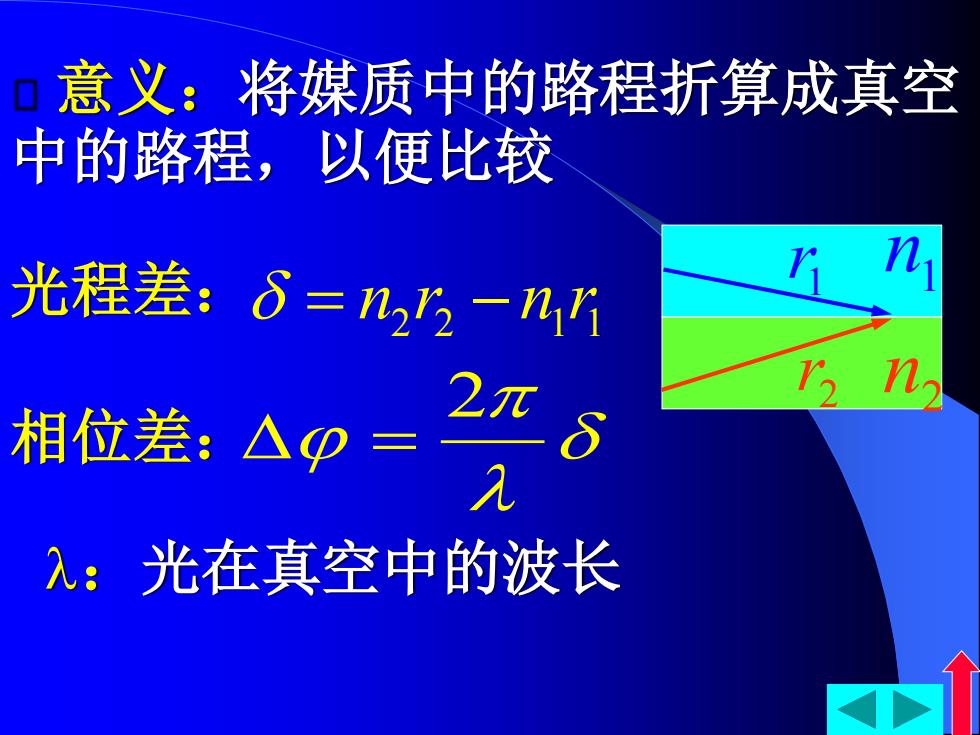
意义:将媒质中的路程折算成真空 中的路程,以便比较 光程差:δ=22-% 相位差:△p 2元 入:光在真空中的波长
n1 n2 意义:将媒质中的路程折算成真空 中的路程,以便比较 光程差: 2 2 1 1 = n r −n r 相位差: 2 = 1 r 2 r :光在真空中的波长

二.透镜的等光程性 口AF和CF在空气 中传播距离长,在 透镜中传播的距离 短邱F则相反 口AF、CF和BF的光程相等,它们会 聚在F点,形成亮点 透镜不会引起附加的光程差
二.透镜的等光程性 F A B C AF和CF在空气 中传播距离长,在 透镜中传播的距离 短BF则相反 AF、CF和BF的光程相等,它们会 聚在F点,形成亮点 透镜不会引起附加的光程差

[例1]在杨氏双缝实验中,用折射率 n=158的透明薄膜盖在上缝上,并用 =6.328×10一7m的光照射,发现中央 明纹向上移动了5条,求薄膜厚度 解:P点为放入薄膜 后中央明纹的位置 .乃3-(-x+x)=0
[例1]在杨氏双缝实验中,用折射率 n=1.58的透明薄膜盖在上缝上,并用 λ=6.32810-7m的光照射,发现中央 明纹向上移动了5条,求薄膜厚度 0 S1 2 S d 2 r 解:P点为放入薄膜 x 后中央明纹的位置 1 r P ( ) 0 r2 − r1 − x + nx =

又因P点是未放薄膜时第N级的位置 .3-乃=N见 可得: N见 X= n-1 5×6.328×10-7 5.46×10 m 1.58-1
又因P点是未放薄膜时第N级的位置 r2 − r1 = N 可得: −1 = n N x 1.58 1 5 6.328 10 7 − = − 5.46 10 m −6 = 0 S1 2 S d 2 r x 1 r P