
3、质点 ·质点的引入 任何物体都有大小和形状。物体在运动时它各部 分的位置变化是不同的,物体的运动情况是非常 复杂的。 质点的概念 当物体的大小和形状忽略不计时,可以把物体当 做只有质量没有形状和大小的点一质点。 •说明 •质点的概念是在考虑主要因素而忽略次要因 素引入的一个理想化的力学模型。 ·一个物体能否当做质点,取决于研究问题的 性质。 那当一个物体不能看成质点时怎么办?
3、质点 •质点的引入 任何物体都有大小和形状。物体在运动时它各部 分的位置变化是不同的,物体的运动情况是非常 复杂的。 •质点的概念 当物体的大小和形状忽略不计时,可以把物体当 做只有质量没有形状和大小的点——质点。 •说明 •质点的概念是在考虑主要因素而忽略次要因 素引入的一个理想化的力学模型。 •一个物体能否当做质点,取决于研究问题的 性质。 那当一个物体不能看成质点时怎么办?
二、位置矢量、运动方程、位移 1、位置矢量 P(xy) 基本概念 从原点O到质点所在的位 置P点的有向线段,叫做 位置矢量或位矢下 r=xiyj X r=vx2+y2 tan X 说明 位置矢量是矢量:有大小和方向; 具有瞬时性; 具有相对性;
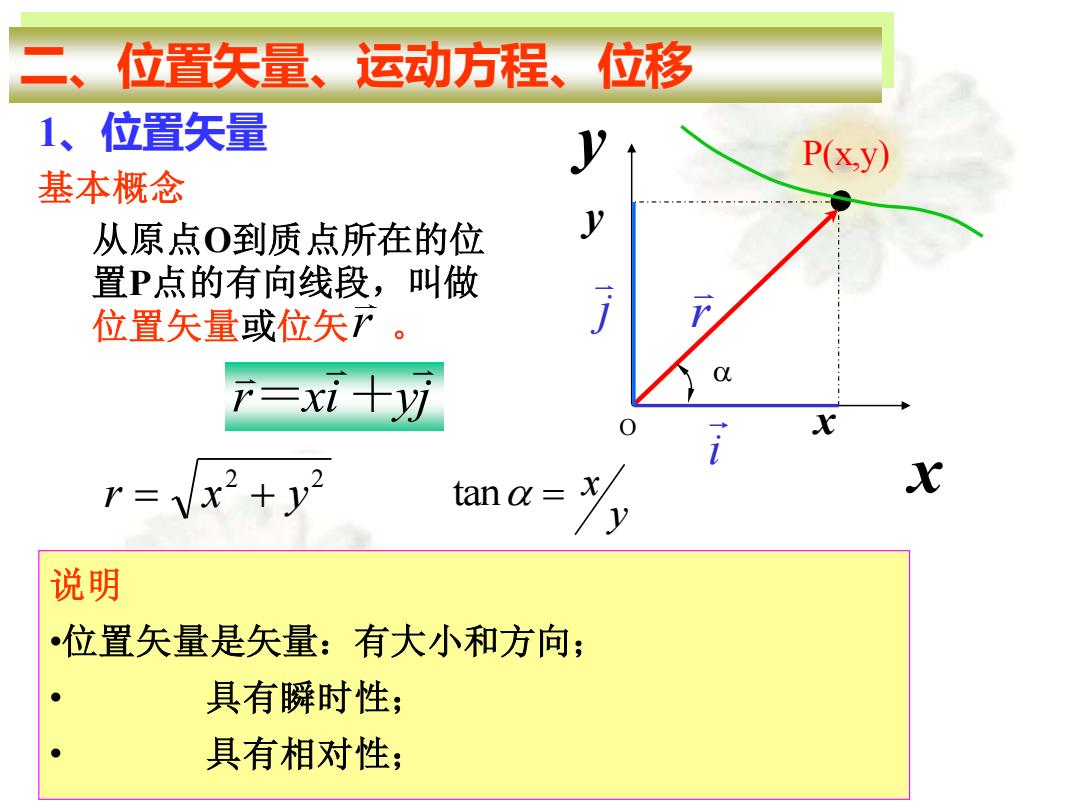
二、位置矢量、运动方程、位移 1、位置矢量 基本概念 从原点O到质点所在的位 置P点的有向线段,叫做 位置矢量或位矢 。 r xi yj = + 2 2 r = x + y y = x tan 说明 •位置矢量是矢量:有大小和方向; • 具有瞬时性; • 具有相对性; O x y P(x,y) r j i x y r
2、j 运动方程、轨迹方程 质点运动时,它相对坐标原点O的位置矢量是随时间变 化的。因此,是时间的函数 F=下(t) y P(t) =x(t)i+y(t)万 J() x=x(t) x() y=y(t) X 运动学的重要任务 质点运动时,在坐标系中描绘的曲 之一,就是找出各 线称为运动的轨迹。 种具体运动所遵循 轨迹是直线:直线运动 的运动方程。 轨迹是曲线:曲线运动
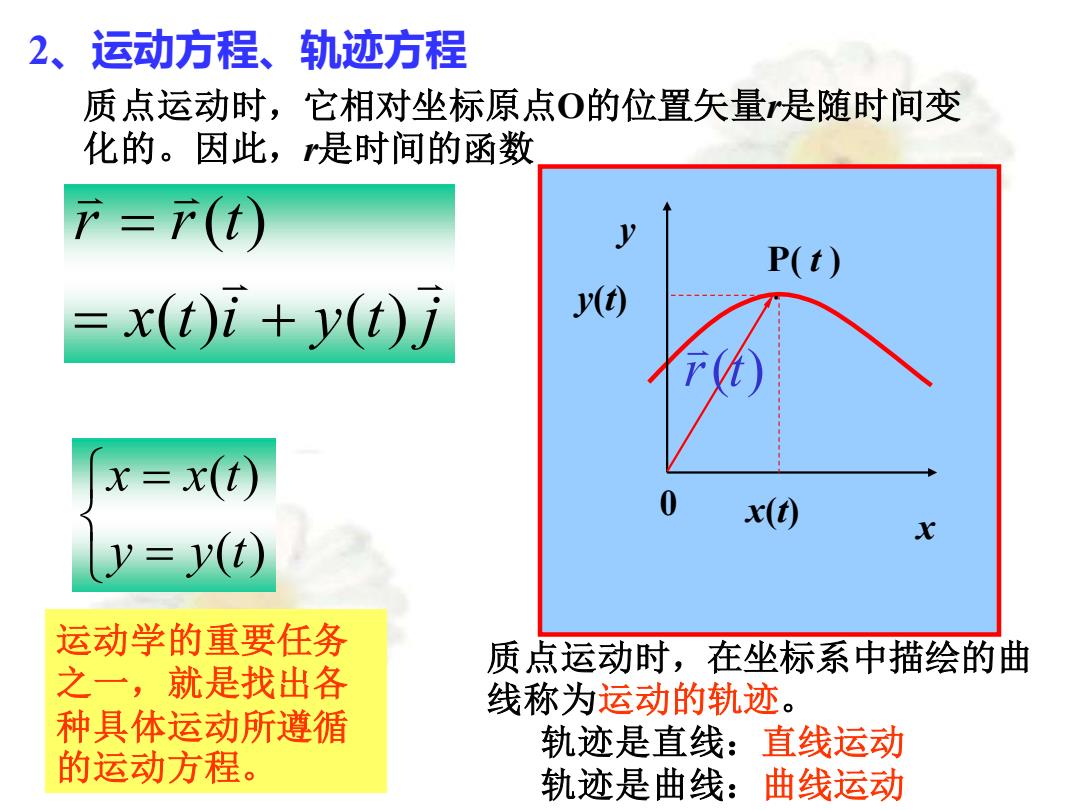
2、运动方程、轨迹方程 质点运动时,它相对坐标原点O的位置矢量r是随时间变 化的。因此,r是时间的函数 x t i y t j r r t ( ) ( ) ( ) = + = = = ( ) ( ) y y t x x t 运动学的重要任务 之一,就是找出各 种具体运动所遵循 的运动方程。 质点运动时,在坐标系中描绘的曲 线称为运动的轨迹。 轨迹是直线:直线运动 轨迹是曲线:曲线运动 x · y y(t) x(t) P( t ) 0 r(t)