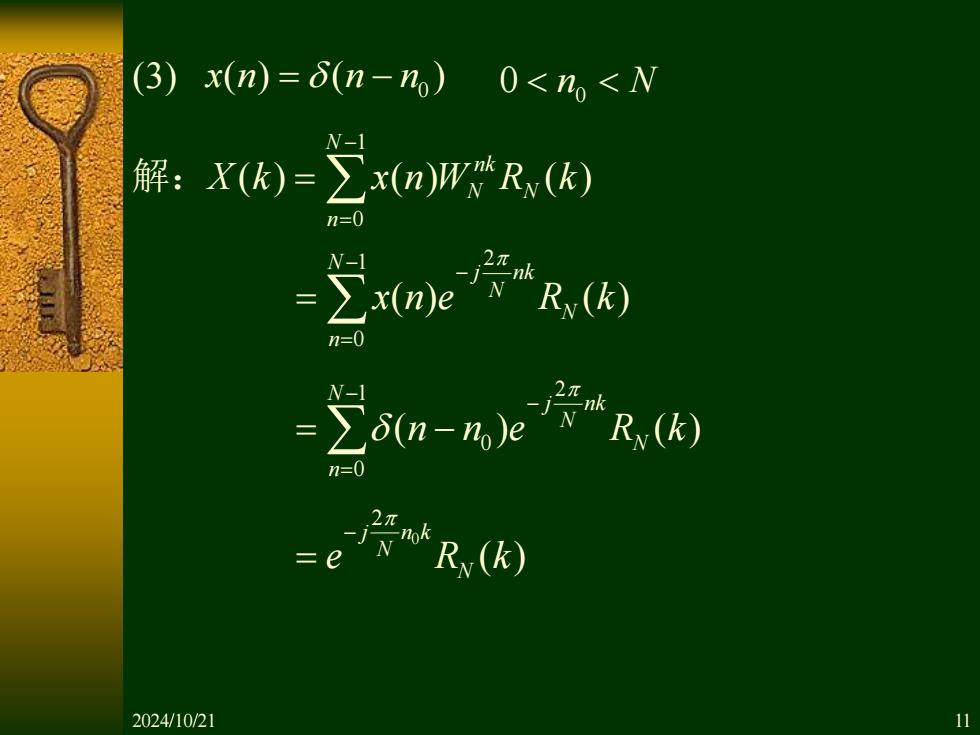
(3)x(n)=δ(n-n)0<n<N 解:X)=∑mW时R,() n=0 e章R,肉 n=0 点0R 2π -e Ry(k) 2024/10/21
1 2 0 ( ) ( ) N j nk N N n x n e R k − − = = 1 2 0 0 ( ) ( ) N j nk N N n n n e R k − − = = − 0 2 ( ) j n k N N e R k − = (3) 0 x n n n ( ) ( ) = − 0 0 n N 1 0 ( ) ( ) ( ) N nk N N n X k x n W R k − = 解: = 2024/10/21 11

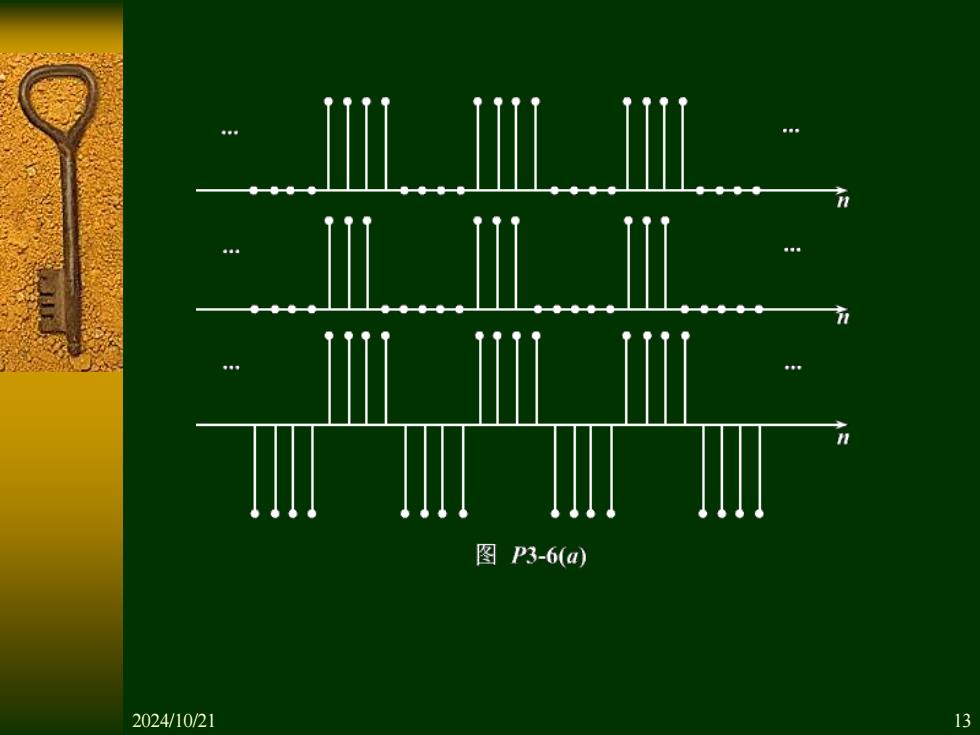
6.如图P3-6(a)画出了几个周期序列x(n),这 些序列可以表示成傅里叶级数 1) 哪些序列能够通过选择时间原点使所有的 X(k)成为实数? 2) 哪些序列能够通过选择时间原点使所有的 ()(除(O)外)成为虚数? 3)哪些序列能做到X(k)=0,k=±2,±4,±6,. 2024/10/21 12
1 (2 / ) 0 1 ( ) ( ) N j N nk k x n X k e N − = = 6. 如图P3-6(a)画出了几个周期序列 ,这 些序列可以表示成傅里叶级数 x n( ) (1)哪些序列能够通过选择时间原点使所有的 X k( ) 成为实数? (2)哪些序列能够通过选择时间原点使所有的 X k( ) (除 X (0) 外)成为虚数? (3)哪些序列能做到 X k( ) 0 = , k = 2, 4, 6,. 2024/10/21 12
图P3-6(a 2024/10/21 13
2024/10/21 13
解:(1)要使()为实数,根据DFT的性质: x(n)=元(n)→ Re[(k ) 元,(n)=0>lm[x(k)]=0 (为共轭对称序列,即满足实部偶对称,虚部 奇对称(以n=0为轴)。 又由图知,x(n)为实序列,虚部为零,故x(n)应 满足偶对称:(n)=(-n) 即(n)是以n=0 为对称轴的偶对称 故第二个序列满足这个条件 2024/10/21
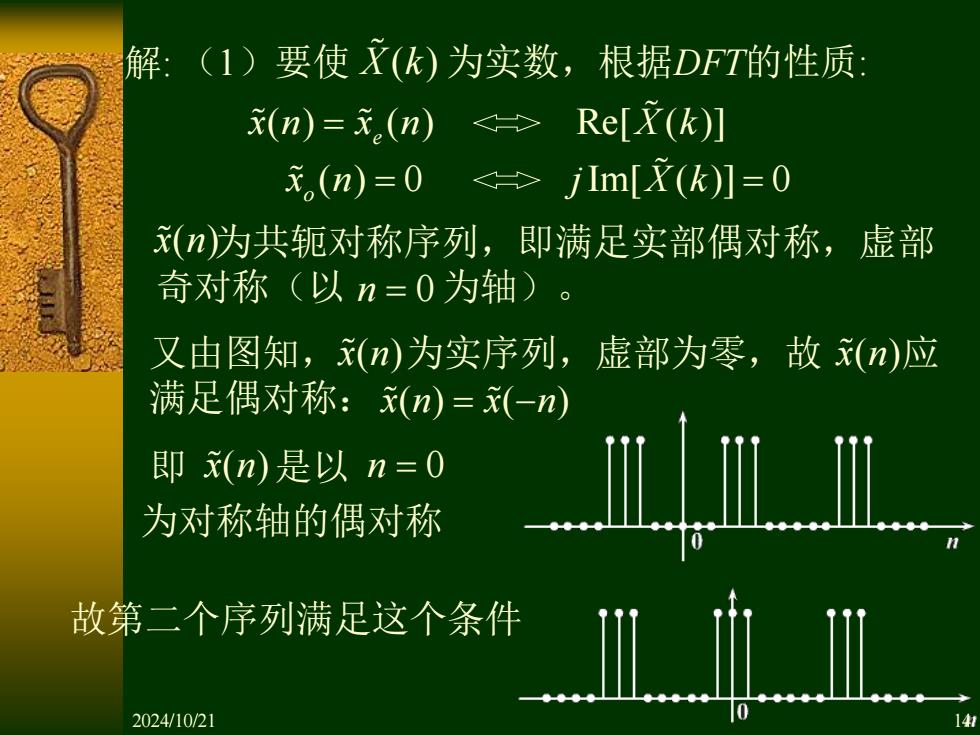
为共轭对称序列,即满足实部偶对称,虚部 奇对称(以 为轴)。 x n( ) n = 0 即 是以 为对称轴的偶对称 x n( ) n = 0 解: (1)要使 X k( ) 为实数,根据DFT的性质: ( ) ( ) Re[ ( )] e x n x n X k = x n j X k o ( ) 0 Im[ ( )] 0 = = x n( ) x n( ) x n x n ( ) ( ) = − 又由图知, 为实序列,虚部为零,故 应 满足偶对称: 故第二个序列满足这个条件 2024/10/21 14

2)要使立(化)为虚数,根据DFT的性质: x(n)=0 Re[X(k)]=0 (n)=,(n) jIm[()] (n)为共轭反对称序列,即满足实部奇对称,虚 部偶对称(以n=0为轴)。 又由图知,x(n)为实序列,虚部为零,故x(n)应 满足奇对称:x(n)=-x(-n) 即x(n)是以n=0对称轴的奇对称 故这三个序列都不满足这个条件 2024/10/21 15
为共轭反对称序列,即满足实部奇对称,虚 部偶对称(以 为轴)。 x n( ) n = 0 即 x n( ) 是以 n = 0 对称轴的奇对称 (2)要使 X k( ) 为虚数,根据DFT的性质: ( ) 0 Re[ ( )] 0 e x n X k = = ( ) ( ) Im[ ( )] o x n x n j X k = x n( ) x n( ) x n x n ( ) ( ) = − − 又由图知, 为实序列,虚部为零,故 应 满足奇对称: 故这三个序列都不满足这个条件 2024/10/21 15