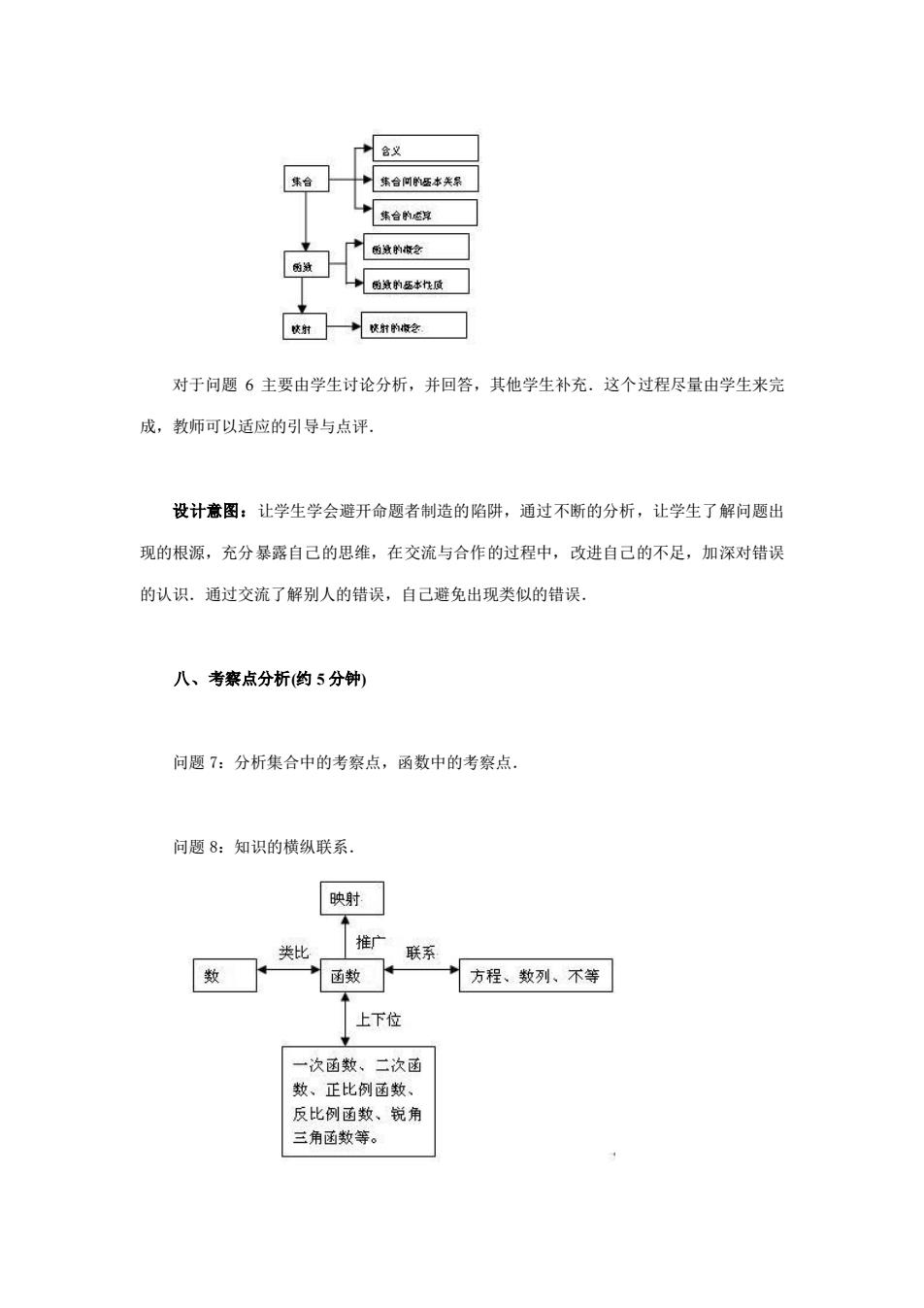
对于问题6主要由学生讨论分析,并回答,其他学生补充。这个过程尽量由学生来完 成,教师可以适应的引导与点评。 设计意图:让学生学会避开命题者制造的陷阱,通过不断的分析,让学生了解问题出 现的根源,充分暴露自己的思维,在交流与合作的过程中,改进自己的不足,加深对错误 的认识。通过交流了解别人的错误,自己避免出现类似的错误 八、考泰点分析(的5分钟) 问题7:分析集合中的考察点,函数中的考察点。 问愿8:知识的横纵联系, 映射 推广 数☐ 类比 联系 西数 方程、效列、不等 上下位 一次函数、二次函 数、正比例函数、 反比例西数、锐角 三角西数等
对于问题 6 主要由学生讨论分析,并回答,其他学生补充.这个过程尽量由学生来完 成,教师可以适应的引导与点评. 设计意图:让学生学会避开命题者制造的陷阱,通过不断的分析,让学生了解问题出 现的根源,充分暴露自己的思维,在交流与合作的过程中,改进自己的不足,加深对错误 的认识.通过交流了解别人的错误,自己避免出现类似的错误. 八、考察点分析(约 5 分钟) 问题 7:分析集合中的考察点,函数中的考察点. 问题 8:知识的横纵联系.

学生回答问题要点预设如下: 1.集合中元素的互异性 2.A二B,则集合A可以是空集」 3.交集与并集的区分,即何时取交,何时取并,特别是含参的分类讨论问题 4.函数的单调性与奇偶性的证明】 5.作业与试卷中出现的问题。 6.学生分析本章的考察点,主要分析考察的知识点、思想方法等方面。 设计意图:让学生了解考察点,才能知道命题者的考察意图,才能选择合适的知识与 思想方法来解答。例如如果试题中出现集合,无论试题以什么形式出现,考察点基本是集 合间的基本关系、集合的运算。 九、典型问题分析 例1:设集合A=(x2+4x=0) B={x天+2a+)x+d2-1=0)(1)若BGA,求实数a的值 (2)若A门B=B,求a的值:
学生回答问题要点预设如下: 1.集合中元素的互异性. 2. ,则集合 A 可以是空集. 3.交集与并集的区分,即何时取交,何时取并,特别是含参的分类讨论问题. 4.函数的单调性与奇偶性的证明. 5.作业与试卷中出现的问题. 6.学生分析本章的考察点,主要分析考察的知识点、思想方法等方面. 设计意图: 让学生了解考察点,才能知道命题者的考察意图,才能选择合适的知识与 思想方法来解答.例如如果试题中出现集合, 无论试题以什么形式出现,考察点基本是集 合间的基本关系、集合的运算. 九、典型问题分析 例 1:设集合 (1)若 ,求实数 的值; (2)若 ,求 的值;

(3)若AUB=B,求a的值,教师点评,同时板书, ()答案:a≤-1或a=1y (2)答案:a=1或a≤1 (3)答案:a=1. 由学生分析问题的考察点,包括知识与数学思想.(预设有以下几个方面)从知识点 来分析,这是集合问题。考察点主要为集合的表示方法、集合中元素的特性、集合间的基 本关系、集合的运算等。学生在解第1个问时,可能漏掉特殊情况。第2、3问可能会遇到 一定的障碍,可以给学生时间进行充分的思考. 设计意图:让学生体会到分析考察点的好处,养成解愿之前分析考察点的习惯。能顺 利的找到问题的突破口,为后续的解答扫清障碍.通过一题多问、一愿多解、多题归一, 让学生主动的形成发散思维,主动应用转化与化归的思想 例2:已知函数(闭是定义在R上的奇函数,当x20时, x)=x1+x),求函数的解析式. 变式:函数是偶函数 教师对生回答进行点评。并板书
(3)若 ,求 的值.教师点评,同时板书. (1)答案: 或 ; (2)答案: 或 ; (3)答案: . 由学生分析问题的考察点,包括知识与数学思想.(预设有以下几个方面)从知识点 来分析,这是集合问题.考察点主要为集合的表示方法、集合中元素的特性、集合间的基 本关系、集合的运算等.学生在解第 1 个问时,可能漏掉特殊情况.第 2、3 问可能会遇到 一定的障碍,可以给学生时间进行充分的思考. 设计意图:让学生体会到分析考察点的好处,养成解题之前分析考察点的习惯.能顺 利的找到问题的突破口,为后续的解答扫清障碍.通过一题多问、一题多解、多题归一, 让学生主动的形成发散思维,主动应用转化与化归的思想. 例 2:已知函数 是定义在 R 上的奇函数,当 时, ,求函数的解析式. 变式:函数是偶函数 教师对生回答进行点评.并板书.

∫x(1+x,x20 f闭=0-.x<0 学生分析考察点、解题思路,如果不完善,其他学生补充. 学生回答问题要点预设如下: 1.考察点为函数的奇偶性与函数图象的关系, 2.函数的奇偶性的定义. 3.转化与化归的思想。 法一:本愿即求x<O,函数的解析式,可先利用函数的奇偶性绘制函数的图象,把本题 转化为二次函数的图象与解析式的问题, 法二:本法更具有一般性,已知 x之0时,函数的解析式,要分析x<0时的函数对应关系,即当一个数小于零时,函数值 应当怎样计算.由于函数具有奇偶性,即一个数与它的相反数的函数值之间有关系 一x>0,所以可以研究一x的函数值。 设计意图:学生在思考的过程中,体会数形结合思想。函数的奇偶性与函数的图象的 关系,可以根据奇偶性绘制函数图象,也可以通过函数的图象分析函数的奇偶性,两者是 相辅相承的。体会转化与化归的思想,把要研究的转化为已知的。考察函数的单调性的证
学生分析考察点、解题思路,如果不完善,其他学生补充. 学生回答问题要点预设如下: 1.考察点为函数的奇偶性与函数图象的关系. 2.函数的奇偶性的定义. 3.转化与化归的思想. 法一:本题即求 ,函数的解析式,可先利用函数的奇偶性绘制函数的图象,把本题 转化为二次函数的图象与解析式的问题. 法二:本法更具有一般性,已知 时,函数的解析式,要分析 时的函数对应关系,即当一个数小于零时,函数值 应当怎样计算.由于函数具有奇偶性,即一个数与它的相反数的函数值之间有关系, ,所以可以研究 的函数值. 设计意图:学生在思考的过程中,体会数形结合思想.函数的奇偶性与函数的图象的 关系,可以根据奇偶性绘制函数图象,也可以通过函数的图象分析函数的奇偶性,两者是 相辅相承的.体会转化与化归的思想,把要研究的转化为已知的.考察函数的单调性的证

明,函数的奇偶性与单调性之间的关系,体会知识的纵向联系。体会转化与化归的思想、 特殊与一般的数学思想,让学生体会到问题后面隐含的本质, 例3:已知了()是偶函数,而且在(0,+0)上是减函数,判断/()在-0,0)上是增函数 还是减函数,并证明你的判断。 变式1:函数为奇函数 变式2:你能分析奇函数(偶函数)在对称区间上的单调性的关系吗?试从数形两个方面来分 析. 学生分析考察点、解题思路,如果不完善,其他学生补充。 学生回答问题要点预设如下: 1,考察点为函数的奇偶性与单调性的关系 2.函数的单调性的定义 3.数形结合、转化与化归的思想。 法一:通过函数的图象分析 法二:把要研究的范围转化为己知的范围
明,函数的奇偶性与单调性之间的关系,体会知识的纵向联系.体会转化与化归的思想、 特殊与一般的数学思想,让学生体会到问题后面隐含的本质. 例 3:已知 是偶函数,而且在 上是减函数,判断 在 上是增函数 还是减函数,并证明你的判断. 变式 1:函数为奇函数 变式 2:你能分析奇函数(偶函数)在对称区间上的单调性的关系吗?试从数形两个方面来分 析. 学生分析考察点、解题思路,如果不完善,其他学生补充. 学生回答问题要点预设如下: 1.考察点为函数的奇偶性与单调性的关系. 2.函数的单调性的定义. 3.数形结合、转化与化归的思想. 法一:通过函数的图象分析. 法二:把要研究的范围转化为已知的范围.