
核心重难探究 解:.'在△ABC和△DCB中,AB=DC,AC=DB,BC=CB, '.△ABC≈△DCB(SSS). 【方法归纳】 在说明三角形全等时,除了充分应用题目提供的条件外,还 应仔细观察图形,充分挖掘题目图形中的隐含条件,如公共边、 公共角、对顶角等 导航页
导航页 核心重难探究 解:∵在△ABC和△DCB中,AB=DC,AC=DB,BC=CB, ∴△ABC≌△DCB(SSS). 【方法归纳】 在说明三角形全等时,除了充分应用题目提供的条件外,还 应仔细观察图形,充分挖掘题目图形中的隐含条件,如公共边、 公共角、对顶角等
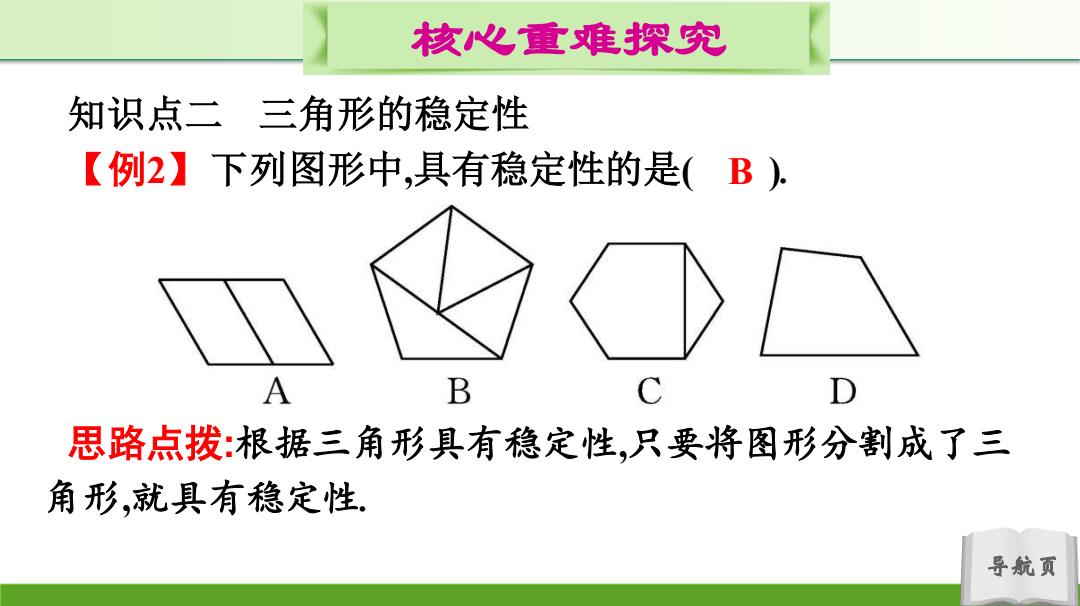
核心重难探究 知识点二三角形的稳定性 【例2】下列图形中,具有稳定性的是(B), A B 思路点拨:根据三角形具有稳定性,只要将图形分割成了三 角形,就具有稳定性。 导航页
导航页 核心重难探究 知识点二 三角形的稳定性 【例2】下列图形中,具有稳定性的是( ). 思路点拨:根据三角形具有稳定性,只要将图形分割成了三 角形,就具有稳定性. B