
其余符号意义同前 ∑fAp cose。+faA,+fm4n=faA (13-24) 由此可求出混凝土截面受压区的面积A。因A是受压区高度x的函数,故截面型式确 定后,斜截面受压区高度x也就不难求得,受压区合力作用点的位置也随之可以确定 预应力混凝土粱斜截面抗弯承载力的计算比较麻烦,因此也可以同普通钢筋混凝土受弯 构件一样,用构造措施来加以保证,具体要求可参照钢筋混凝土梁的有关内容。 13.3预加力的计算与预应力损失的估算 设计预应力混凝土受弯构件时,需要事先根据承受外荷载的情况,估定其预加应力的大 小。由于施工因素、材料性能和环境条件等的影响,钢筋中的预拉应力会逐渐减少。这种预 应力钢筋的预应力随着张拉、锚固过程和时间推移而降低的现象称为预应力损失。设计中所 需的钢筋预应力值,应是扣除相应阶段的应力损失后,钢筋中实际存余的预应力(有效预应 力。)值。如果钢筋初始张拉的预应力(一般称为张拉控制应力)为Om,相应的应力损 失值为,则它们与有效预应力间的关系为 0x=0m-0 (13-25) 13.3.1钢筋的张拉控制应力 张拉控制应力是指预应力钢筋错固前张拉钢筋的千斤顶所显示的总拉力除以预应 力钢筋截面积所求得的钢筋应力值。对于有锚圈口摩阻损失的锚具,σ应为扣除锚圈口 摩擦损失后的锚下拉应力值,故《公路桥规》特别指出,G为张拉钢筋的锚下控制应力 从提高预应力钢筋的利用率来说,张拉控制应力O应尽量定高些,使构件混凝土获 得较大的预压应力值以提高构件的抗裂性,同时可以减少钢筋用量。但·又不能定得过 高,以免个别钢筋在张拉或施工过程中被拉,而且。值增高,钢筋的应力松损失也 将增大。另外,高应力状态使构件可能出现纵向裂缝:并且过高的应力也降低了构件的延性。 因此。不宜定得过高,一般宜定在钢筋的比例极限以下。不同性质的预应力筋应分别确 定其值,对于钢丝与钢绞线,因拉伸应力一应变曲线无明显的屈服台阶,其m与抗 拉强度标准值∫:的比值应相应地定得低些:而精轧螺纹钢筋,一般具有较明显的屈服台阶, 塑性性能较好,故其比值可相应地定得高些。《公路桥规》规定,构件预加应力时预应力钢 13-11
13-11 其余符号意义同前。 水平投影长度 C 确定后,尚应确定受压区合力作用点的位置 O,以便确定各力臂的长 度。由斜截面的受力平衡条件 H = 0 ,可得到 cos pd pb p sd s pd p cd c + + = f A f A f A f A (13-24) 由此可求出混凝土截面受压区的面积 A c 。因 A c 是受压区高度 x 的函数,故截面型式确 定后,斜截面受压区高度 x 也就不难求得,受压区合力作用点的位置也随之可以确定。 预应力混凝土梁斜截面抗弯承载力的计算比较麻烦,因此也可以同普通钢筋混凝土受弯 构件一样,用构造措施来加以保证,具体要求可参照钢筋混凝土梁的有关内容。 13.3 预加力的计算与预应力损失的估算 设计预应力混凝土受弯构件时,需要事先根据承受外荷载的情况,估定其预加应力的大 小。由于施工因素、材料性能和环境条件等的影响,钢筋中的预拉应力会逐渐减少。这种预 应力钢筋的预应力随着张拉、锚固过程和时间推移而降低的现象称为预应力损失。设计中所 需的钢筋预应力值,应是扣除相应阶段的应力损失后,钢筋中实际存余的预应力(有效预应 力 pe )值。如果钢筋初始张拉的预应力(一般称为张拉控制应力)为 con ,相应的应力损 失值为 l ,则它们与有效预应力 pe 间的关系为 pe = con − l (13-25) 13.3.1 钢筋的张拉控制应力 张拉控制应力 con 是指预应力钢筋锚固前张拉钢筋的千斤顶所显示的总拉力除以预应 力钢筋截面积所求得的钢筋应力值。对于有锚圈口摩阻损失的锚具, con 应为扣除锚圈口 摩擦损失后的锚下拉应力值,故《公路桥规》特别指出, con 为张拉钢筋的锚下控制应力。 从提高预应力钢筋的利用率来说,张拉控制应力 con 应尽量定高些,使构件混凝土获 得较大的预压应力值以提高构件的抗裂性,同时可以减少钢筋用量。但 con 又不能定得过 高,以免个别钢筋在张拉或施工过程中被拉断,而且 con 值增高,钢筋的应力松弛损失也 将增大。另外,高应力状态使构件可能出现纵向裂缝;并且过高的应力也降低了构件的延性。 因此 con 不宜定得过高,一般宜定在钢筋的比例极限以下。不同性质的预应力筋应分别确 定其 con 值,对于钢丝与钢绞线,因拉伸应力-应变曲线无明显的屈服台阶,其 con 与抗 拉强度标准值 pk f 的比值应相应地定得低些;而精轧螺纹钢筋,一般具有较明显的屈服台阶, 塑性性能较好,故其比值可相应地定得高些。《公路桥规》规定,构件预加应力时预应力钢

筋在构件端部(锚下)的控制应力。应符合下列规定: 对于钢丝、钢绞线 0m≤0.75fpt (13-26 对于精轧螺纹钢筋 oom≤0.90fnt (13-27) 式中∫,为预应力钢筋的抗拉强度标准值。 在实际工程中,对于仅需在短时间内保持高应力的钢筋,例如为了减少一些因素引起的 应力损失,而需要进行超张拉的钢筋,可以适当提高张拉应力,但在任何情况下,钢筋的最 大张拉控制应力,对于钢丝、纲饺线不应超过0.8∫:对于精轧螺纹钢筋不应超过0.95: 13.3.2钢筋预应力损失的估算 预应力损失与施工工艺、材料性能及环境影响等有关,影响因素复杂,一般应根据实验 数据确定,如无可靠试验资料,则可按《公路桥规》的规定估算。 一般情况下,可主要考虑以下六项应力损失值。但对于不同锚具、不同施工方法,可能 还存在其他预应力损失,如错圈口摩阻损失等,应根据具体情况逐项考虑其影响 1)预应力筋与管道壁间摩擦引起的应力损失(0:) 后张法的预应力筋,一般由直线段和曲线段组成。张拉时,预应力筋将沿管道壁滑移而 产生摩擦图13-8,使钢筋中的预拉应力形成张拉端高,向构件跨中方向逐渐减小[图 13-8b的情况。钢筋在任意两个截面间的应力差值,就是这两个截面间由摩擦所引起的预应 力损失值。从张拉端至计算截面的摩擦应力损失值以σ,表示。 摩擦损失主要由管道的弯曲和管道位置偏差引起的。对于直线管道,由于施工中位置偏 差和孔壁不光滑等原因,在钢筋张拉时,局部孔壁也将与钢筋接触从而引起摩擦损失,一般 称此为管道偏差影响(或称长度影响)摩擦损失,其数值较 :对于弯曲部分的管道,除存 在上述管道偏差影响之外,还存在因管道弯转,预应力筋对弯道内啦的经向压力所起的摩擦 损失,将此称为弯道影响摩擦损失,其数值较大,并随钢筋弯曲角度之和的增加而增加。曲 线部分摩擦损失是由以上两部分影响构成的,故要比直线部分摩擦损失大得多。 13-12
13-12 筋在构件端部(锚下)的控制应力 con 应符合下列规定: 对于钢丝、钢绞线 con ≤0.75 pk f (13-26) 对于精轧螺纹钢筋 con ≤0.90 pk f (13-27) 式中 pk f 为预应力钢筋的抗拉强度标准值。 在实际工程中,对于仅需在短时间内保持高应力的钢筋,例如为了减少一些因素引起的 应力损失,而需要进行超张拉的钢筋,可以适当提高张拉应力,但在任何情况下,钢筋的最 大张拉控制应力,对于钢丝、纲绞线不应超过 0.8 pk f ;对于精轧螺纹钢筋不应超过 0.95 pk f 。 13.3.2 钢筋预应力损失的估算 预应力损失与施工工艺、材料性能及环境影响等有关,影响因素复杂,一般应根据实验 数据确定,如无可靠试验资料,则可按《公路桥规》的规定估算。 一般情况下,可主要考虑以下六项应力损失值。但对于不同锚具、不同施工方法,可能 还存在其他预应力损失,如锚圈口摩阻损失等,应根据具体情况逐项考虑其影响。 1)预应力筋与管道壁间摩擦引起的应力损失( l1 ) 后张法的预应力筋,一般由直线段和曲线段组成。张拉时,预应力筋将沿管道壁滑移而 产生摩擦力[图 13-8a)],使钢筋中的预拉应力形成张拉端高,向构件跨中方向逐渐减小[图 13-8b)]的情况。钢筋在任意两个截面间的应力差值,就是这两个截面间由摩擦所引起的预应 力损失值。从张拉端至计算截面的摩擦应力损失值以 l1 表示。 摩擦损失主要由管道的弯曲和管道位置偏差引起的。对于直线管道,由于施工中位置偏 差和孔壁不光滑等原因,在钢筋张拉时,局部孔壁也将与钢筋接触从而引起摩擦损失,一般 称此为管道偏差影响(或称长度影响)摩擦损失,其数值较小;对于弯曲部分的管道,除存 在上述管道偏差影响之外,还存在因管道弯转,预应力筋对弯道内壁的径向压力所起的摩擦 损失,将此称为弯道影响摩擦损失,其数值较大,并随钢筋弯曲角度之和的增加而增加。曲 线部分摩擦损失是由以上两部分影响构成的,故要比直线部分摩擦损失大得多
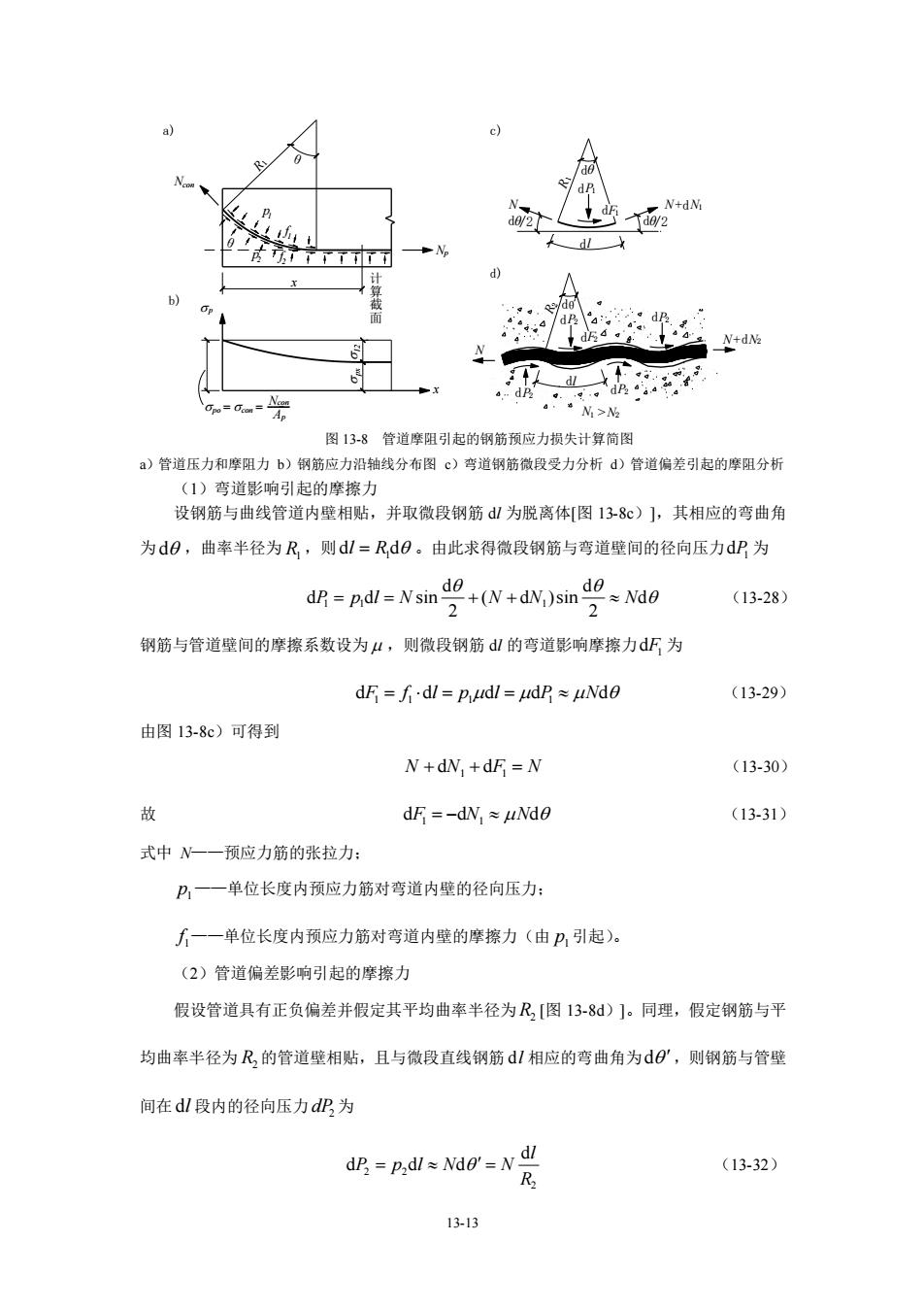
d 6 -Gum-m 图13-8管道摩阻引起的钢筋预应力损失计算简图 )管道压力和摩阳力b)钢筋应力沿轴线分布图©)弯道钢筋微段受力分析d)管道偏差引起的摩阻分析 (1)弯道影响引起的摩擦力 设钢筋与曲线管道内壁相贴,并取微段钢筋山为脱离体[图138c)],其相应的弯曲角 为dB,曲率半径为R,则dl=R,d0。由此求得微段钢筋与弯道壁间的径向压力dP为 dr=pdl=Nsin (N+dN)sin o=Ndo (13-28) 2 钢筋与管道壁间的摩擦系数设为4,则微段钢筋d!的弯道影响摩擦力d5为 dF=fdl=p udl=udp uNdo (13-29) 由图13-8c)可得到 N+dN,+dF=N (13-30) df=-dW,≈uNde (13-31) 式中N一一预应力筋的张拉力: P,一一单位长度内预应力筋对弯道内壁的径向压力: 人一一单位长度内预应力筋对弯道内壁的摩擦力(由P引起) (2)管道偏差影响引起的摩擦力 假设管道具有正负偏差并假定其平均曲率半径为R[图13-8d)]。同理,假定钢筋与平 均曲率半径为R的管道壁相贴,且与微段直线钢筋d!相应的弯曲角为d©,则钢筋与管壁 间在d山段内的径向压力d识为 d识=pa=0g=N光 (13-32) 13-13
13-13 dθ /2 d d d /2 计 算 截 面 d dθ θ a) θ c) d) b) p po p N A = con = px l2 con f 1 2 p f 2 1 p Ncon Np x N N+ N1 F1 P1 R1 dl dP2 dF2 dP2 N dP2 dP2 N1 N2 x 2 R 1 R > dl dθ θ N+dN2 ---- ` 图 13-8 管道摩阻引起的钢筋预应力损失计算简图 a)管道压力和摩阻力 b)钢筋应力沿轴线分布图 c)弯道钢筋微段受力分析 d)管道偏差引起的摩阻分析 (1)弯道影响引起的摩擦力 设钢筋与曲线管道内壁相贴,并取微段钢筋 dl 为脱离体[图 13-8c)],其相应的弯曲角 为 d ,曲率半径为 R1 ,则 1 d d l R = 。由此求得微段钢筋与弯道壁间的径向压力 1 dP 为 1 1 1 d d d d sin ( d )sin d 2 2 P p l N N N N = = + + (13-28) 钢筋与管道壁间的摩擦系数设为 ,则微段钢筋 dl 的弯道影响摩擦力 1 dF 为 1 1 1 1 d d d d d F f l p l P N = = = (13-29) 由图 13-8c)可得到 1 1 N N F N + + = d d (13-30) 故 1 1 d d d F N N = − (13-31) 式中 N——预应力筋的张拉力; 1 p ——单位长度内预应力筋对弯道内壁的径向压力; 1 f ——单位长度内预应力筋对弯道内壁的摩擦力(由 1 p 引起)。 (2)管道偏差影响引起的摩擦力 假设管道具有正负偏差并假定其平均曲率半径为 R2 [图 13-8d)]。同理,假定钢筋与平 均曲率半径为 R2 的管道壁相贴,且与微段直线钢筋 dl 相应的弯曲角为 d ,则钢筋与管壁 间在 dl 段内的径向压力 2 dP 为 2 2 2 d d d d l P p l N N R = = (13-32)

故dl段内的摩擦力dF,为 的=ud明*w是 (13-33) 令k=4R,为管道的偏差系数,则 dF3 =k.N.dl =-dN2 (13-34) (3)弯道部分的总摩擦力 预应力钢筋在管道弯曲部分微段d!内的摩擦力为上述两部分之和,即 dF=dF+dF N.(ud0+kdl) (13-35) (4)钢筋计算截面处因摩擦力引起的应力损失值 由微段钢筋轴向力的平衡可得到 dN,+dN,+dF+dF =0 (13-36) 故 dNdN,+dN,=-dF-dF =-N(ud0+kdl) 或写成 兴-0+ (13-37) 将上式两边同时积分可得到 In N=-(u0+kl)+c 由张拉端边界条件:O==0,L=L=0时,则N=Nm,代入上式可得到c=lnNn, 于是 In N =-(ue+kl)+In Nm (13-38) 亦即 N In =-(u0+k N=Ncoe e-(o) (13-39) 为计算方便,式中1近似地用其在构件纵轴上的投影长度x代替,则上式为 Nx =Ncon ek) (13-40) 式中N,为距张拉端为x的计算截面处,钢筋实际的张拉力。 由此可求得因摩擦所引起的预应力损失值·为 -=a-e (13-41) A。 式中Oom一一错下张拉控制应力,Om=Nm/A。,Nm为钢筋错下张拉控制力: 1314
13-14 故 dl 段内的摩擦力 2 dF 为 2 2 2 d d d l F P N R = (13-33) 令 R2 k = 为管道的偏差系数,则 2 2 d d d F k N l N = = − (13-34) (3)弯道部分的总摩擦力 预应力钢筋在管道弯曲部分微段 dl 内的摩擦力为上述两部分之和,即 1 2 d d d ( d d ) F F F N k l = + = + (13-35) (4)钢筋计算截面处因摩擦力引起的应力损失值 l1 由微段钢筋轴向力的平衡可得到 1 2 1 2 d d d d 0 N N F F + + + = (13-36) 故 1 2 1 2 d d d d d ( d d ) N N N F F N k l = + = − − = − + 或写成 d ( d d ) N k l N = − + (13-37) 将上式两边同时积分可得到 ln N = −( + kl) + c 由张拉端边界条件: = 0 = 0,L = L0 = 0 时,则 N N= con ,代入上式可得到 con c N = ln , 于是 con ln ( ) ln N kl N = − + + (13-38) 亦即 con ln ( ) N kl N = − + 故 ( k ) con l N N e − + = (13-39) 为计算方便,式中 l 近似地用其在构件纵轴上的投影长度 x 代替,则上式为 ( ) con kx N N e x − + = (13-40) 式中 Nx 为距张拉端为 x 的计算截面处,钢筋实际的张拉力。 由此可求得因摩擦所引起的预应力损失值 l1 为 con ( ) 1 1 x kx l con p N N e A − − + = = − (13-41) 式中 con ——锚下张拉控制应力, con con = N Ap , Ncon 为钢筋锚下张拉控制力;

A。一—预应力钢筋的藏面面积: 0一从张拉端至计算截面间管道平面曲线的夹角[图13-8)]之和,即曲线包角 按绝对值相加,单位以弧度计。如管道为竖平面内和水平面内同时弯曲的三维 空间曲线管道,则日可按式(13-42)计算: 0=V0%+0 (13-42) 、,一一分别为在同段管道水平面内的弯曲角与竖向平面内的弯曲角: x一从张拉端至计算截面的管道长度在构件纵轴上的投影长度:或为三维空间曲线 管道的长度,以m计: k -管道每米长度的局部偏差对摩擦的影响系数,可按明表2.5采用 4一一钢筋与管道壁间的摩擦系数,可按附表2-5采用。 为减少摩擦损失, 一般可采用如下措施: (1)采用两端张拉,以减小日值及管道长度x值: (2)采用超张拉。对于后张法预应力钢筋,其张拉工艺按下列要求进行: 对于钢绞线束 0→初应力0.1-0.15o左右句→1.05o(特荷2min)→o(锚固) 对于钢丝束 0→初应力(0.1~0.15o左右句))→1.05o(特荷2min)→0→(锚個) 由于超张拉5%~10%,使构件其他截面应力也相应提高,当张拉力回降至0时,钢 筋因要回缩而受到反向摩擦力的作用,对于简支梁来说,这个回缩影响一般不能传递到受力 最大的跨中截面(或者影响很小),这样跨中截面的预加应力也就因超张拉而获得了稳定的 提高。 应当注意,对于一般夹片式锚具,不宜采用超张拉工艺。因为它是一种钢筋回缩自锚式 锚具,超张拉后的钢筋拉应力无法在锚周前回降至,一回降钢筋就回缩,同时就会带 动夹片进行锚固。这样就相当于提高了·m值,而与超张拉的意义不符。 2)锚具变形、钢筋回缩和接缝压缩引起的应力损失(2) 后张法构件,当张拉结束并进行错固时,锚具将受到巨大的压力并使锚具自身及锚下垫 板压密而变形,同时有些错具的预应力钢筋还要向内回缩:此外,拼装式构件的接缝,在锚 固后也将继续被压密变形,所有这些变形都将使错固后的预应力钢筋放松,因而引起应力损 失,用o2表示,可按下式计算: On-EN E (13-43) 式中Σ△W一一张拉端锚具变形、钢筋回缩和接缝压缩值之和(mm),可根据试验确定,当 无可靠资料时,按附表2-6采用: 1一一张拉端至锚周端之间的距离(mm): 13-15
13-15 A p ——预应力钢筋的截面面积; ——从张拉端至计算截面间管道平面曲线的夹角[图 13-8a)]之和,即曲线包角, 按绝对值相加,单位以弧度计。如管道为竖平面内和水平面内同时弯曲的三维 空间曲线管道,则 可按式(13-42)计算: 2 2 = H + V (13-42) H 、 V ——分别为在同段管道水平面内的弯曲角与竖向平面内的弯曲角; x ——从张拉端至计算截面的管道长度在构件纵轴上的投影长度;或为三维空间曲线 管道的长度,以 m 计; k ——管道每米长度的局部偏差对摩擦的影响系数,可按附表 2-5 采用; ——钢筋与管道壁间的摩擦系数,可按附表 2-5 采用。 为减少摩擦损失,一般可采用如下措施: (1)采用两端张拉,以减小 值及管道长度 x 值; (2)采用超张拉。对于后张法预应力钢筋,其张拉工艺按下列要求进行: 对于钢绞线束 0 (0.1 ~ 0.15 ) 1.05 2min → → → 初应力 con con con 左右 (持荷 ) (锚固) 对于钢丝束 0 (0.1 ~ 0.15 ) 1.05 2min 0 ( → → → → 初应力 con con con 左右 (持荷 ) 锚固) 由于超张拉 5%~10%,使构件其他截面应力也相应提高,当张拉力回降至 con 时,钢 筋因要回缩而受到反向摩擦力的作用,对于简支梁来说,这个回缩影响一般不能传递到受力 最大的跨中截面(或者影响很小),这样跨中截面的预加应力也就因超张拉而获得了稳定的 提高。 应当注意,对于一般夹片式锚具,不宜采用超张拉工艺。因为它是一种钢筋回缩自锚式 锚具,超张拉后的钢筋拉应力无法在锚固前回降至 con ,一回降钢筋就回缩,同时就会带 动夹片进行锚固。这样就相当于提高了 con 值,而与超张拉的意义不符。 2)锚具变形、钢筋回缩和接缝压缩引起的应力损失( l 2 ) 后张法构件,当张拉结束并进行锚固时,锚具将受到巨大的压力并使锚具自身及锚下垫 板压密而变形,同时有些锚具的预应力钢筋还要向内回缩;此外,拼装式构件的接缝,在锚 固后也将继续被压密变形,所有这些变形都将使锚固后的预应力钢筋放松,因而引起应力损 失,用 l 2 表示,可按下式计算: l EP l l 2 = (13-43) 式中 l ——张拉端锚具变形、钢筋回缩和接缝压缩值之和(mm),可根据试验确定,当 无可靠资料时,按附表 2-6 采用; l ——张拉端至锚固端之间的距离(mm);