第6章轴心受压构件的正截面承载力计算 当构件受到位于截面形心的轴向压力作用时,称为轴心受压构件。在实际结构中,严格 的轴心受压构件是很少的,通常由于实际存在的结构节点构造、混凝土组成的非均匀性、纵 向钢筋的布置以及施工中的误差等原因,轴心受压构件截面都或多或少存在弯矩的作用。但 是,在实际 工程中,例 钢筋混凝 桁架拱中 杆件(如受压腹杆 可以按轴心受 构件设计的:同时,由于轴心受压构件计算简便,故可作为受压构件初步估算截面、复核承 载力的手段。 钢筋混凝土轴心受压构件按照箍筋的功能和配置方式的不同可分为两种: 1)配有纵向制筋和普师锛筋的轴心受压构件(普通箍筋柱),如图6-1a)所示 2)配有纵向钢筋和螺旋箍筋的轴心受压构件(螺旋箍筋柱),如图6-b)所示 普通箍筋柱的截面形状多为正方形、矩形和圆形等。纵向钢筋为对称布置,沿构件高度 设置等间距的箍筋。轴心受压构件的承载力主要由混凝土提供,设置纵向钢筋的目的是为了 (1)协助混凝土承受压力,可减少构件截面尺寸:(2)承受可能存在的不大的弯矩:(3) 防止构件的突然胎性破坏。普通筛筋作用是,防止纵向钢筋局部压屈,并与纵向钢筋形成钢 筋骨架,便于施工。 向钢 图61两种钢筋混凝土轴受压构件 a普通箍筋柱b)螺旋箍筋柱 螺旋箍筋柱的截面形状多为圆形或正多边形,纵向钢筋外围设有连续环绕的间距较密的 螺旋箍筋(或间距较密的焊接环形箍筋)。螺旋箍筋的作用是使截面中间部分(核心)混凝 土成为约束混凝土,从而提高构件的承载力和延性。 6.1配有纵向钢筋和普通箍筋的轴心受压构件 6.1.1破坏形态 按照构件的长细比不同,轴心受压构件可分为短柱和长柱两种,它们受力后的侧向变形 和破坏形态各不相同。下面结合有关试验研究来分别介绍。 在轴心受压构件试验中,试件的材料强度级别、截面尺寸和配筋均相同,但柱长度不同 (图6-2)。轴心力P用油压千斤顶施加,并用电子秤量测压力大小。由平衡条件可知,压 力P的读数就等于试验柱截面所受到的轴心压力N值。同时,在柱长度一半处设置百分表, 6-1
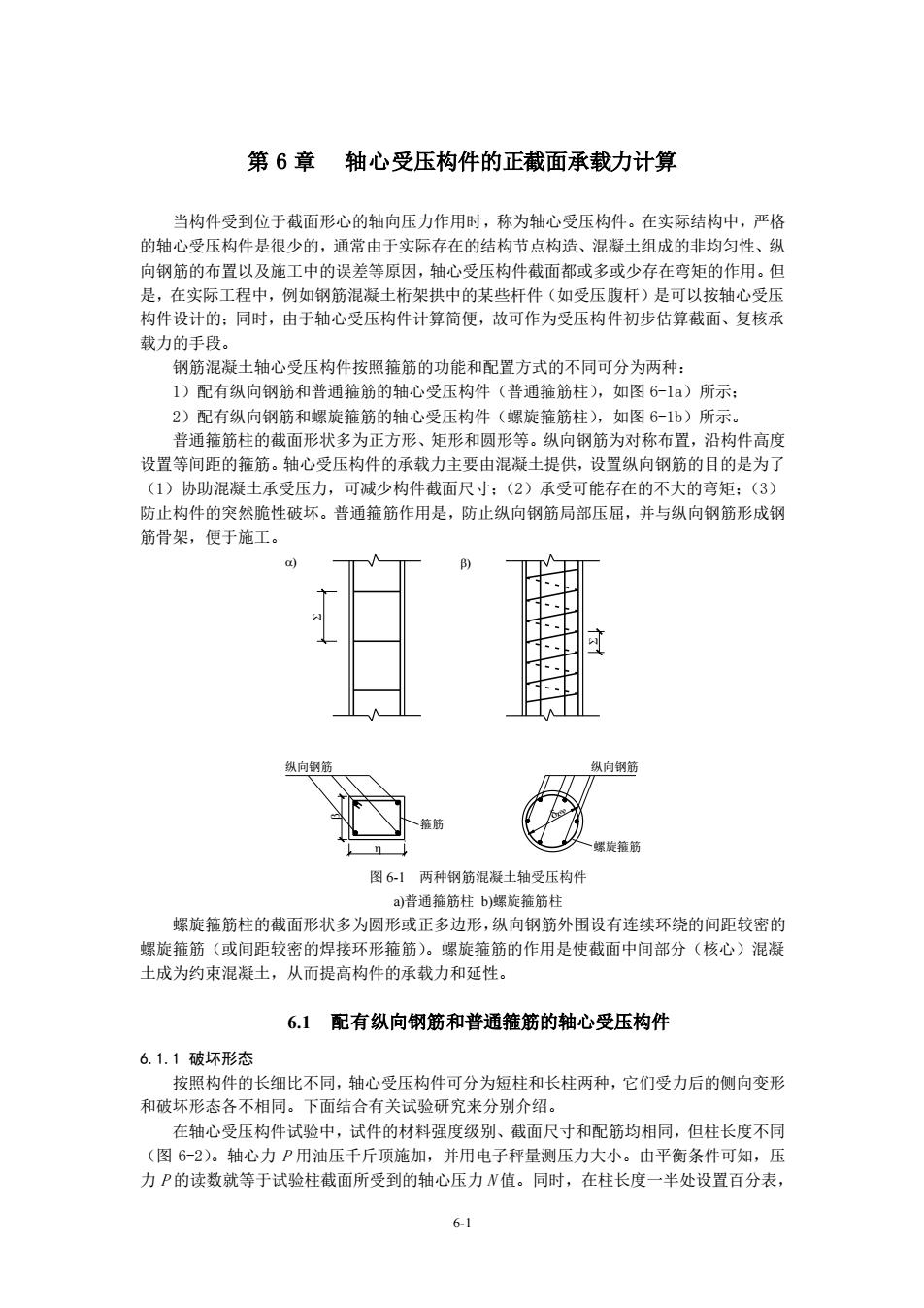
6-1 第 6 章 轴心受压构件的正截面承载力计算 当构件受到位于截面形心的轴向压力作用时,称为轴心受压构件。在实际结构中,严格 的轴心受压构件是很少的,通常由于实际存在的结构节点构造、混凝土组成的非均匀性、纵 向钢筋的布置以及施工中的误差等原因,轴心受压构件截面都或多或少存在弯矩的作用。但 是,在实际工程中,例如钢筋混凝土桁架拱中的某些杆件(如受压腹杆)是可以按轴心受压 构件设计的;同时,由于轴心受压构件计算简便,故可作为受压构件初步估算截面、复核承 载力的手段。 钢筋混凝土轴心受压构件按照箍筋的功能和配置方式的不同可分为两种: 1)配有纵向钢筋和普通箍筋的轴心受压构件(普通箍筋柱),如图 6-1a)所示; 2)配有纵向钢筋和螺旋箍筋的轴心受压构件(螺旋箍筋柱),如图 6-1b)所示。 普通箍筋柱的截面形状多为正方形、矩形和圆形等。纵向钢筋为对称布置,沿构件高度 设置等间距的箍筋。轴心受压构件的承载力主要由混凝土提供,设置纵向钢筋的目的是为了 (1)协助混凝土承受压力,可减少构件截面尺寸;(2)承受可能存在的不大的弯矩;(3) 防止构件的突然脆性破坏。普通箍筋作用是,防止纵向钢筋局部压屈,并与纵向钢筋形成钢 筋骨架,便于施工。 纵向钢筋 ) 纵向钢筋 箍筋 螺旋箍筋 ) 图 6-1 两种钢筋混凝土轴受压构件 a)普通箍筋柱 b)螺旋箍筋柱 螺旋箍筋柱的截面形状多为圆形或正多边形,纵向钢筋外围设有连续环绕的间距较密的 螺旋箍筋(或间距较密的焊接环形箍筋)。螺旋箍筋的作用是使截面中间部分(核心)混凝 土成为约束混凝土,从而提高构件的承载力和延性。 6.1 配有纵向钢筋和普通箍筋的轴心受压构件 6.1.1 破坏形态 按照构件的长细比不同,轴心受压构件可分为短柱和长柱两种,它们受力后的侧向变形 和破坏形态各不相同。下面结合有关试验研究来分别介绍。 在轴心受压构件试验中,试件的材料强度级别、截面尺寸和配筋均相同,但柱长度不同 (图 6-2)。轴心力 P 用油压千斤顶施加,并用电子秤量测压力大小。由平衡条件可知,压 力 P 的读数就等于试验柱截面所受到的轴心压力 N 值。同时,在柱长度一半处设置百分表

测量其横向挠度“。通过对比试验的方法,观察长细比不同的轴心受压构件的破坏形态。 1)短柱 当轴向力P逐浙渐增加时,试件A柱(图62)也随之缩短,测量结果证明混凝土全截面 和纵向钢筋均发生压缩变形。 当轴向力P达到破坏荷载的9%左右时,柱中部四周混凝土表面出现纵向裂缝,部分混 凝土保护层剥落,最后是筛筋间的纵向钢流发生屈曲,向外鼓出,混凝士被压碎而整个试哈 柱破坏(图6-3)。破坏时,测得的混凝土压应变大于1.8×103,而柱中部的横向挠度很小 钢筋混凝土短柱的破坏是 一种材料破坏,即混凝土压碎破坏 6 图6-2轴心受压构件试件(尺寸单位:mm) 图63轴心受压短柱的破坏形态 a)短柱的破坏b)局部放大图 许多试验证明,钢筋混凝土短柱破坏时混凝土的压应变均在2×10附近,由混凝士受 压时的应力应变曲线(图1-10)可知,混凝土已达到其轴心抗压强度:同时,采用普通热 轧的纵向钢筋,均能达到抗压屈服强度。对于高强度钢筋,混凝土应变到达2×10时,钢 筋可能尚未达到屈服强度,在设计时如果采用这样的钢材,则它的抗压强度设计值仅为 0.002E,=0.002×2.0×105=400MPa,即必须小于其抗拉强度设计值来取用。 根据轴向力平衡,就可求得短柱破坏时的轴心力P,,它应由钢筋和混凝土共同负担: P=fA+A (6-1) 2)长柱 试件B柱在压力P不大时,也是全截面受压,但随者压力增大,长柱不仅发生压缩变形, 同时长柱中部产生较大的横向挠度,凹侧压应力较大,凸侧较小。在长柱破坏前,横向挠 度增加得很快,使长柱的破坏来得比较突然,导致失稳破坏。破坏时,凹侧的混凝土首先被 压碎,有混凝土表面纵向裂缝,纵向钢筋被压弯而向外鼓出,混凝土保护层脱落:凸侧则由 受压突然转变为受拉,出现横向裂缝(图64)
6-2 测量其横向挠度 u 。通过对比试验的方法,观察长细比不同的轴心受压构件的破坏形态。 1)短柱 当轴向力 P 逐渐增加时,试件 A 柱(图 6-2)也随之缩短,测量结果证明混凝土全截面 和纵向钢筋均发生压缩变形。 当轴向力 P 达到破坏荷载的 90%左右时,柱中部四周混凝土表面出现纵向裂缝,部分混 凝土保护层剥落,最后是箍筋间的纵向钢筋发生屈曲,向外鼓出,混凝土被压碎而整个试验 柱破坏(图 6-3)。破坏时,测得的混凝土压应变大于 1.8×10-3,而柱中部的横向挠度很小。 钢筋混凝土短柱的破坏是一种材料破坏,即混凝土压碎破坏。 Ⅰ Ⅰ 柱 柱 Ⅰ Ⅰ 剖面Ⅰ−Ⅰ 图 6-2 轴心受压构件试件(尺寸单位:mm) 图 6-3 轴心受压短柱的破坏形态 a)短柱的破坏 b)局部放大图 许多试验证明,钢筋混凝土短柱破坏时混凝土的压应变均在 2×10-3 附近,由混凝土受 压时的应力应变曲线(图 1-10)可知,混凝土已达到其轴心抗压强度;同时,采用普通热 轧的纵向钢筋,均能达到抗压屈服强度。对于高强度钢筋,混凝土应变到达 2×10-3 时,钢 筋可能尚未达到屈服强度,在设计时如果采用这样的钢材,则它的抗压强度设计值仅为 0.002 0.002 2.0 10 400MPa 5 Es = = ,即必须小于其抗拉强度设计值来取用。 根据轴向力平衡,就可求得短柱破坏时的轴心力 Ps ,它应由钢筋和混凝土共同负担: ' s ' Ps = f c A+ f s A (6-1) 2)长柱 试件 B 柱在压力 P 不大时,也是全截面受压,但随着压力增大,长柱不仅发生压缩变形, 同时长柱中部产生较大的横向挠度 u ,凹侧压应力较大,凸侧较小。在长柱破坏前,横向挠 度增加得很快,使长柱的破坏来得比较突然,导致失稳破坏。破坏时,凹侧的混凝土首先被 压碎,有混凝土表面纵向裂缝,纵向钢筋被压弯而向外鼓出,混凝土保护层脱落;凸侧则由 受压突然转变为受拉,出现横向裂缝(图 6-4)。 Ps a) 短柱的混凝土破坏 b)局部方大图 P s
T 图64轴心受压长柱的破坏形态 长柱的破坏b)局部放大图 图6-5为短柱和长柱试验的横向挠度u与轴向力P之间关系的对比图。 n(KN) (KN) B性 Wμμ) O(B) 图6-5轴心受压构件的横向挠度4 a横向挠度沿柱长的变化b)横向挠度!与轴心压力P的关系 由图65及大量的其它试验可知,短柱总是受压破坏,长柱则是失稳破坏:长柱的承载 力要小于相同截面、配筋、材料的短柱承载力。因此,可以将短柱的承载力乘以一个折减系 数口来表示相同截面、配筋和材料的长柱承载力B: P=0P. (6-2) 3
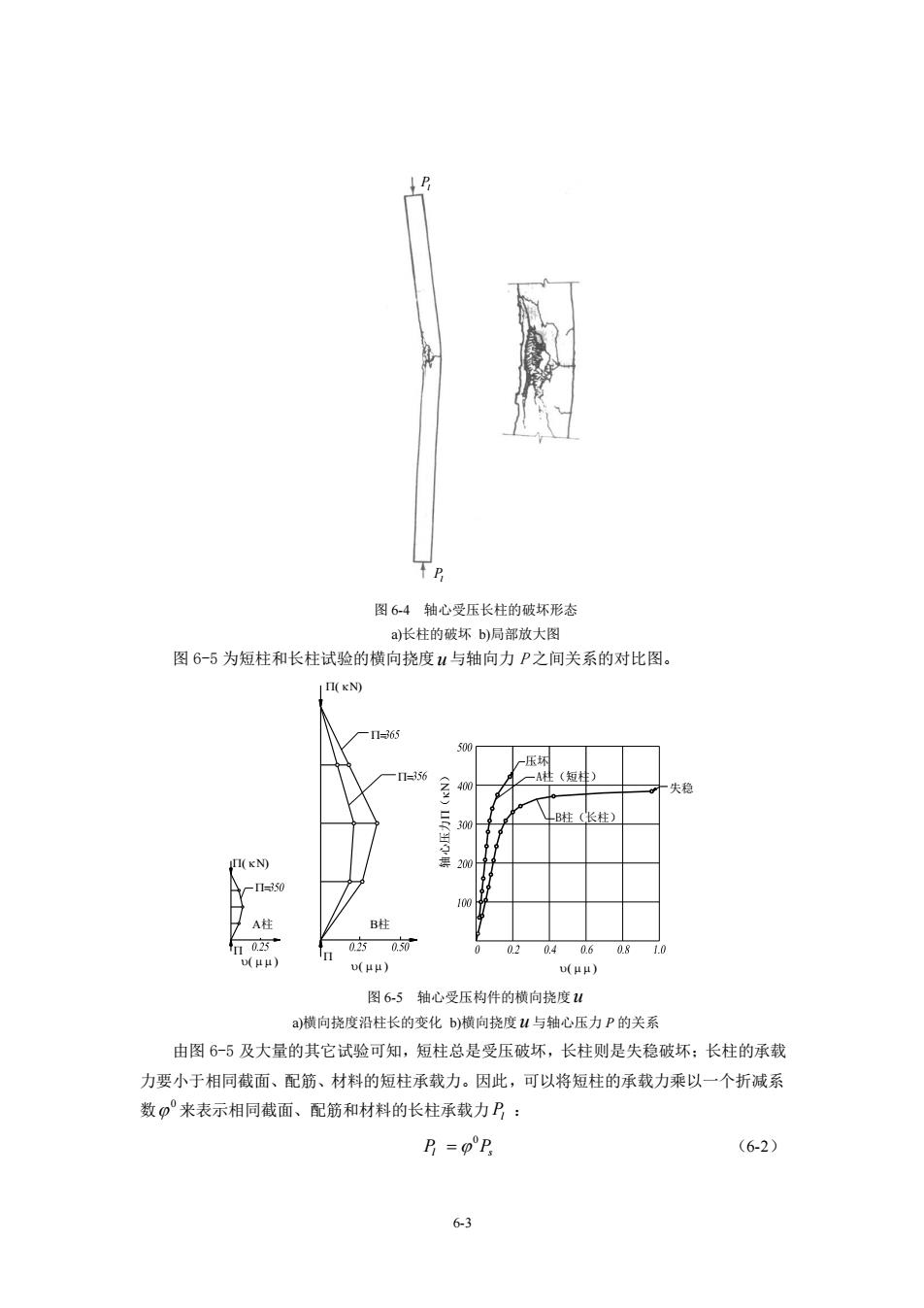
6-3 图 6-4 轴心受压长柱的破坏形态 a)长柱的破坏 b)局部放大图 图 6-5 为短柱和长柱试验的横向挠度 u 与轴向力 P 之间关系的对比图。 = ( ) ( ) = ( ) ( ) = 轴心压力( ) B柱(长柱) A柱(短柱) 压坏 ( ) 失稳 柱 柱 图 6-5 轴心受压构件的横向挠度 u a)横向挠度沿柱长的变化 b)横向挠度 u 与轴心压力 P 的关系 由图 6-5 及大量的其它试验可知,短柱总是受压破坏,长柱则是失稳破坏;长柱的承载 力要小于相同截面、配筋、材料的短柱承载力。因此,可以将短柱的承载力乘以一个折减系 数 0 来表示相同截面、配筋和材料的长柱承载力 Pl : 0 P P l s = (6-2) Pl Pl

式中P一一短柱破坏时的轴心压力: D一一相同截面、配筋和材料的长柱失稳时的轴心压力: 6.1.2稳定系数0 钢筋混疑土轴心受压构件计算中,考虑构件长细比增大的附加效应使构件承载力降低的 计算系数称为轴心受压构件的稳定系数,用符号口表示。如前所述,稳定系数就是长柱失稳 破坏时的临界承载力力D与短柱压坏时的轴心力P的比值,表示长柱承载力降低的程度。 根据材料力学,各种支承条件柱的临界压力计算式为 h=z'tl (6-3) 式中E1一一柱截面的抗弯刚度: 。一一柱的计算长度。 将式(6-3)和式(61)代入式(6-2)中,可得到 EI xEl F26UA+5④6AU+fP (6-4) 式中一子A为鞋激凝士面积。《为城向销销的酸面积 在式(6-4)中,E为柱截面的抗弯刚度,是材料在弹性阶段的刚度。对钢筋混凝土米 说,由于长柱失稳时截面往往已经开裂,刚度大大降低,大约为弹性阶段的30%一50%,所以 式(6-4)中的EI值要改用柱裂缝出现后的刚度,即用B,EI来代替式(6-4)中的E以,B 为柱刚度折减系数。于是,可得到 影河骆元 π2BEL (6-5) 柱截面回转半径r=√1A,长细比2=1r,以p、fa、∫a分别代替p°、厂。 ∫,则式(65)成为 π2月E。1 p-a+p元 (6-6) 显然,由式(6-6)可以看到,当柱的材料和纵筋含筋率一定时,随着长细比入的增加, 稳定系数口值就减小,相应的长柱破坏时临界力P也愈小。 稳定系数口主要与构件的长细比有关,混凝土强度等级及配筋率p对其影响较小。《公 路桥规》根据国内试验资料,考虑到长期荷载作用的影响和荷载初偏心影响,规定了稳定系 6.4
6-4 式中 Ps ——短柱破坏时的轴心压力; Pl ——相同截面、配筋和材料的长柱失稳时的轴心压力; 6.1.2 稳定系数 钢筋混凝土轴心受压构件计算中,考虑构件长细比增大的附加效应使构件承载力降低的 计算系数称为轴心受压构件的稳定系数,用符号 表示。如前所述,稳定系数就是长柱失稳 破坏时的临界承载力力 Pl 与短柱压坏时的轴心力 Ps 的比值,表示长柱承载力降低的程度。 根据材料力学,各种支承条件柱的临界压力计算式为 2 0 2 l EI Pl = (6-3) 式中 EI ——柱截面的抗弯刚度; 0 l ——柱的计算长度。 将式(6-3)和式(6-1)代入式(6-2)中,可得到 ( ) ( ) 2 2 0 2 ' ' 2 ' ' 0 0 l s c s s c s P EI EI P l f A f A l A f f = = = + + (6-4) 式中 A As ' ' = , A 为柱混凝土面积, ' As 为纵向钢筋的截面积。 在式(6-4)中,EI 为柱截面的抗弯刚度,是材料在弹性阶段的刚度。对钢筋混凝土来 说,由于长柱失稳时截面往往已经开裂,刚度大大降低,大约为弹性阶段的 30%~50%,所以 式(6-4)中的 EI 值要改用柱裂缝出现后的刚度,即用 c c E I 1 来代替式(6-4)中的 EI,1 为柱刚度折减系数。于是,可得到 ( ) 2 0 ' ' 1 2 2 ' ' 0 1 2 0 Al I f f E l A f f E I c c s c c s c c + = + = (6-5) 柱截面回转半径 / c r I A = ,长细比 0 = l r/ ,以 、 cd f 、 ' sd f 分别代替 0 、 c f 、 ' s f ,则式(6-5)成为 2 1 ' ' 2 c 1 cd sd E f f = + (6-6) 显然,由式(6-6)可以看到,当柱的材料和纵筋含筋率一定时,随着长细比 的增加, 稳定系数 值就减小,相应的长柱破坏时临界力 Pl 也愈小。 稳定系数 主要与构件的长细比有关,混凝土强度等级及配筋率 ' 对其影响较小。《公 路桥规》根据国内试验资料,考虑到长期荷载作用的影响和荷载初偏心影响,规定了稳定系

数0值(附表110).由附表1-10可以看到,长细比元=上(矩形截面)越大,p值越小, 当务≤8时,=1。构件的承载力设有降经,即为短挂。 查表求口值时,必须要知道构件的计算长度6,可参照表6-1取用。在实际桥梁设计中, 应根据具体构造选择构件端部约束条件,进而获得符合实际的计算长度。值。 构件纵向弯曲计算长度,值 表6 杆件 构件及其两定情况 计算长度 两编固定 051 直杆 一端因定,一猪为不移动较 0.71 两编均为不移动校 10/ 端定,一自由 201 注:一构件支点间长度: 6.1.3正截面承载力计算 《公路桥规》规定配有纵向受力钢筋和普通箍筋的轴心受压构件正截面承载力计算式为 YoN,N.=0.9o(fA+f4) (6-7) 式中N,一一轴向力组合设计值: 0 -轴心受压构件稳定系数,按附表1-10取用: A一一构件毛截面面积: A,一一全部纵向钢筋截面面积。 ∫一一混凝士轴心抗压强度设计值: 厂一—纵向普通钢筋抗压强度设计值。 图66普通箍筋柱正截面承载力计算图式
6-5 数 值(附表 1-10)。由附表 1-10 可以看到,长细比 b l 0 = (矩形截面)越大, 值越小, 当 b l 0 ≤8 时, ≈1,构件的承载力没有降低,即为短柱。 查表求 值时,必须要知道构件的计算长度 l0,可参照表 6-1 取用。在实际桥梁设计中, 应根据具体构造选择构件端部约束条件,进而获得符合实际的计算长度 l0 值。 构件纵向弯曲计算长度 l0 值 表 6-1 杆件 构件及其两端固定情况 计算长度 l0 直杆 两端固定 0.5l 一端固定,一端为不移动铰 0.7 l 两端均为不移动铰 1.0 l 一端固定,一端自由 2.0 l 注:l—构件支点间长度; 6.1.3 正截面承载力计算 《公路桥规》规定配有纵向受力钢筋和普通箍筋的轴心受压构件正截面承载力计算式为 0Nd ≤ ( ) ' ' u 0.9 cd sd As N = f A + f (6-7) 式中 Nd ——轴向力组合设计值; ——轴心受压构件稳定系数,按附表 1-10 取用; A ——构件毛截面面积; ' As ——全部纵向钢筋截面面积。 cd f ——混凝土轴心抗压强度设计值; ' sd f ——纵向普通钢筋抗压强度设计值。 ' ' ' 图 6-6 普通箍筋柱正截面承载力计算图式