
理想低通抽样的证明 6(t0=) òt-nM)d,(oj22o-@, n=-00 m,))=m06,d)=∑mnT,)6t-nI,) n=-0 .()- Mo)*∑o=n@,) M(o=n,) N=-00 N=-0 7
7 ( ) ( ) T s n t t nT =− = − =− = − n s s T n T ( ) 2 ( ) =− = = − n s T s nTs m (t) m(t) (t) m(nT ) (t ) ( )* ( ) 1 () T s s M T M = 理想低通抽样的证明 = − N=− s s M n T ( )* ( ) 1 = − N=− s s M n T ( ) 1
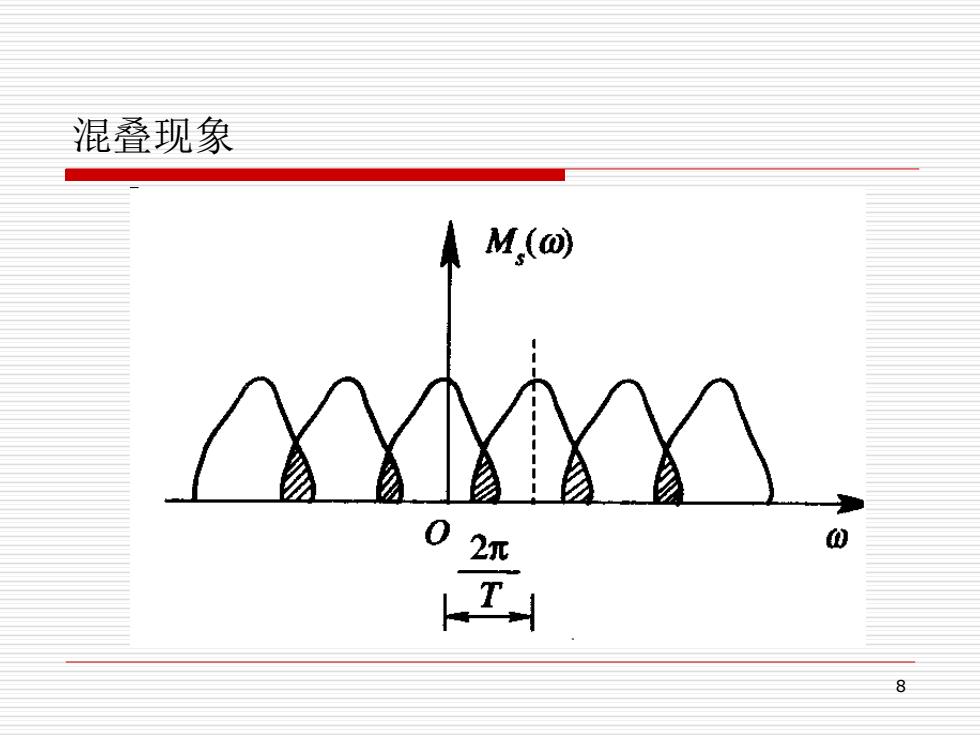
混叠现象 M,(o 0 2 工 6
8 混叠现象
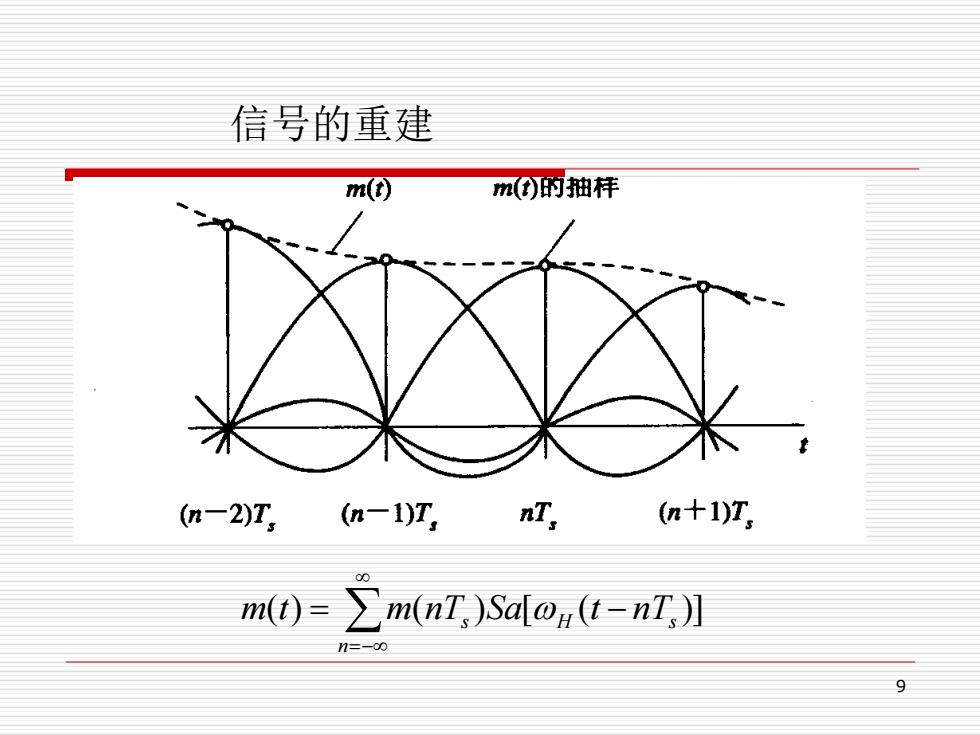
信号的重建 m(t) m)的抽样 (n-2)T,(n-1)T, n十1)T mt)=∑mnI,)Sado,t-nT,】 9
9 信号的重建 =− = − n s H nTs m(t) m(nT )Sa[ (t )]
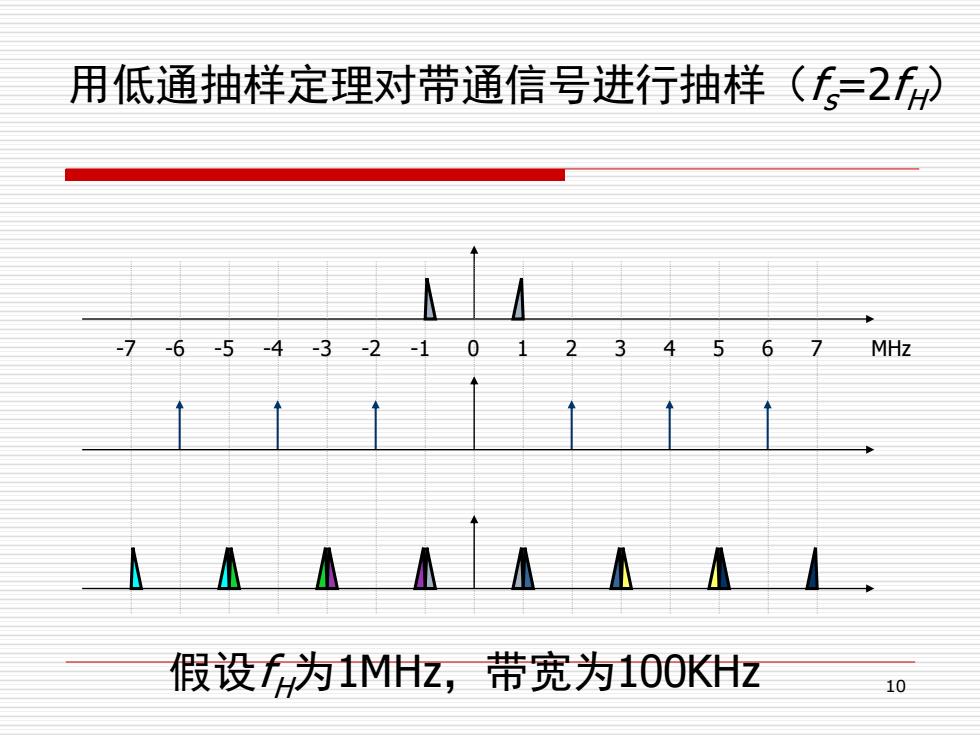
用低通抽样定理对带通信号进行抽样((=2f) 7-6-5-43-2-1 0 234567MHz 假设f为MHz,带宽为100KHz 10
10 用低通抽样定理对带通信号进行抽样(fs=2fH) -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 假设fH为1MHz,带宽为100KHz MHz

带通信号抽样定理 一个带通信号m(①), 其频率限制在f与,之间, 带宽为B=, 如果抽样速率f。2fm, m是一个不超过f/B的最大整数, 那么m)可完全由其抽样值确定。 11
11 带通信号抽样定理 一个带通信号m(t), 其频率限制在fL与fH之间, 带宽为 B=fH −fL, 如果抽样速率 f s=2fH /m, m是一个不超过 fH /B 的最大整数, 那么m(t)可完全由其抽样值确定