
通信原理 第12章正交编码与伪随机序列 1
1 通信原理 第12章 正交编码与伪随机序列

第12章正交编码与伪随机序列 引言 正交编码与伪随机序列在数字通信技术中都 是十分重要的。正交编码不仅可以用作纠错 编码,还可以用来实现码分多址通信,目前 已经广泛用于蜂窝网中。伪随机序列在误码 率测量、时延测量、扩谱通信、密码及分离 多径等方面都有着十分广泛的应用。因此 本章将在简要讨论正交编码概念之后,着重 讨论伪随机序列及其应用。 2
2 第12章 正交编码与伪随机序列 ⚫ 引言 正交编码与伪随机序列在数字通信技术中都 是十分重要的。正交编码不仅可以用作纠错 编码,还可以用来实现码分多址通信,目前 已经广泛用于蜂窝网中。伪随机序列在误码 率测量、时延测量、扩谱通信、密码及分离 多径等方面都有着十分广泛的应用。因此, 本章将在简要讨论正交编码概念之后,着重 讨论伪随机序列及其应用

第12章正交编码与伪随机序列 12.2正交编码 "12.2.1正交编码的基本概念 ◆正交性 口若两个周期为T的模拟信号s1()和s2()互相正交,则有 s,0s,0h=0 同理,若M个周期为的模拟信号s1(),S2(),., 5()构成一个正交信号集合,则有 s()s.(d=0 i≠ji,j=1,2,.,M ◆互相关系数 ·对于二进制数字信号,用一数字序列表示码组。这里 我们只讨论二进制且码长相同的编码。这时,两个码 组的正交性可用如下形式的互相关系数来表述
3 第12章 正交编码与伪随机序列 ⚫ 12.2 正交编码 ◼ 12.2.1 正交编码的基本概念 ◆ 正交性 若两个周期为T的模拟信号s1 (t)和s2 (t)互相正交,则有 同理,若M个周期为T的模拟信号s1 (t),s2 (t),., sM(t)构成一个正交信号集合,则有 ◆ 互相关系数 对于二进制数字信号,用一数字序列表示码组。这里, 我们只讨论二进制且码长相同的编码。这时,两个码 组的正交性可用如下形式的互相关系数来表述。 = T s t s t dt 0 1 ( ) 2 ( ) 0 = T s t s t dt 0 1 ( ) 2 ( ) 0 i j;i, j=1, 2, ., M

第12章正交编码与伪随机序列 设长为的编码中码元只取值+1和-1,以及x和y是其中两个码 组: X=(X1,X2,x3,.,xn) y=(y1,y2,y3,.,yn) 其中 x,y∈(+1,-1)。 i=1,2,.,n 则x和y间的互相关系数定义为 p(.)= n i=l 若码组x和正交,则必有p(x,y)=0
4 第12章 正交编码与伪随机序列 设长为n的编码中码元只取值+1和-1,以及x和y是其中两个码 组: 其中 则x和y间的互相关系数定义为 若码组x和y正交,则必有(x, y) = 0。 ( , , , , ) 1 2 3 n x = x x x x ( , , , , ) 1 2 3 n y = y y y y xi , yi (+1,−1), i =1,2, ,n = = n i i i x y n x y 1 1 ( , )
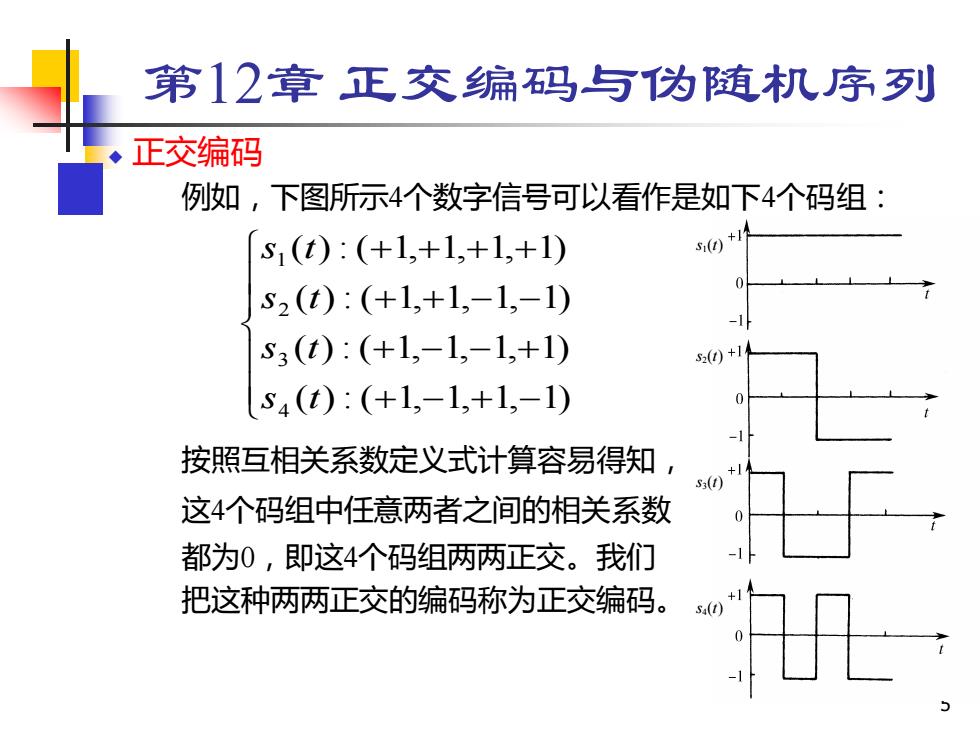
第12章正交编码与伪随机序列 正交编码 例如,下图所示4个数字信号可以看作是如下4个码组: S1(t):(+1,+1,+1,+1) S2(t):(+1,+1,-1,-1) -1 S3(t):(+1,-1,-1,+1) 0+1 S4(t):(+1,-1,+1,-1) 按照互相关系数定义式计算容易得知 S3(t) 这4个码组中任意两者之间的相关系数 都为0,即这4个码组两两正交。我们 把这种两两正交的编码称为正交编码。 s4()
5 第12章 正交编码与伪随机序列 ◆ 正交编码 例如,下图所示4个数字信号可以看作是如下4个码组: 按照互相关系数定义式计算容易得知, 这4个码组中任意两者之间的相关系数 都为0,即这4个码组两两正交。我们 把这种两两正交的编码称为正交编码。 s1(t) s2(t) s3(t) s4(t) + − + − + − − + + + − − + + + + ( ) : ( 1, 1, 1, 1) ( ) : ( 1, 1, 1, 1) ( ) : ( 1, 1, 1, 1) ( ) : ( 1, 1, 1, 1) 4 3 2 1 s t s t s t s t