数学建模（学习笔记）一种基于对流扩散方程的有风烟尘扩散数值模拟方法

期末作业 Final assignment 2023年5月28日 数学建模课程 May 28th,2023 整理得迭代公式（此处将无量纲化的风速U记为） C做-cdk+CA-Cd+票C1-C-d (4.2) C++C-+n+ 这个公式对时间向前差分的，而对空间中心差分，因此称作Foward Time and Central Space(FTCS)格式。根据带误差的形式可看出它对时间有一阶误差，对空间则有二阶误差。 4.2.3C-N格式 为了在时间上也达到二阶误差，可以采用Crank-Nicolson(CN)格式，表达式如下： CCCCC-Ca-) +0Cnua+Cua+CL-Ci-+c吃n+C1-6Cd +票c-Cd+c-0 (4.3) +0(c+ci+c-Cu+c+C--6C) 容易看出，这个式子事实上是在相邻的时间上计算了FTCS差分的更新步长，并将两个 步长进行了平均。通过泰勒展开分析可以证明，这个做法的误差对时间也是二阶的。由于式 子中不止出现了一个第1+1步的值，事实上需要将上标1+1的项移植左侧，联合边界条件 得到方程组，并通过方程组求解下一步的值。 这种需要求解方程得到下一步值的方法称为隐式方法，而FSTC这类可以直接计算的 格式则称为显式方法。不难想到，隐式方法的计算开销会远远高于显式方法，但可以保证更 高的精度。 S4.3稳定性分析 在运用迭代格式进行求解之前，一般需要先进行稳定性的分析来确保迭代的有效。我们 采用常用的von Neumman分析方法进行考察，以此确定h,与h的基本取值。 4.3.1 von Neumman方法 一般来说，当其他都已经固定时，任何有效的方法只要：充分小都能做到稳定，但若 :取得过大，哪怕对于很简单的方程，也会产生无法控制的误差。例如，考虑方程 ac 0m=0r2-0 (4.4) 对初值C0,)=sim(,取h=高，h:=斋进行FTCS的前几次选代效果如图1

期末作业 2023 年 5 月 28 日 数学建模课程 Final Assignment May 28th, 2023 整理得迭代公式（此处将无量纲化的风速 U 记为 v） C l+1 i,j,k =C l i,j,k + vht 2h (C l i+1,j,k − C l i−1,j,k) + w l kht 2h (C l i,j,k+1 − C l i,j,k−1 ) + Dht h 2 (C l i+1,j,k + C l i−1,j,k + C l i,j+1,k − C l i,j−1,k + C l i,j,k+1 + C l i,j,k−1 − 6C l i,j,k) (4.2) 这个公式对时间向前差分的，而对空间中心差分，因此称作 Foward Time and Central Space(FTCS) 格式。根据带误差的形式可看出它对时间有一阶误差，对空间则有二阶误差。 4.2.3 C-N 格式 为了在时间上也达到二阶误差，可以采用 Crank-Nicolson(C-N) 格式，表达式如下： C l+1 i,j,k =C l i,j,k + 1 2 ( vht 2h (C l i+1,j,k − C l i−1,j,k) + w l kht 2h (C l i,j,k+1 − C l i,j,k−1 ) + Dht h 2 (C l i+1,j,k + C l i−1,j,k + C l i,j+1,k − C l i,j−1,k + C l i,j,k+1 + C l i,j,k−1 − 6C l i,j,k) + vht 2h (C l+1 i+1,j,k − C l+1 i−1,j,k) + w l+1 k ht 2h (C l+1 i,j,k+1 − C l+1 i,j,k−1 ) + Dht h 2 (C l+1 i+1,j,k + C l+1 i−1,j,k + C l+1 i,j+1,k − C l+1 i,j−1,k + C l+1 i,j,k+1 + C l+1 i,j,k−1 − 6C l+1 i,j,k) ) (4.3) 容易看出，这个式子事实上是在相邻的时间上计算了 FTCS 差分的更新步长，并将两个 步长进行了平均。通过泰勒展开分析可以证明，这个做法的误差对时间也是二阶的。由于式 子中不止出现了一个第 l + 1 步的值，事实上需要将上标 l + 1 的项移植左侧，联合边界条件 得到方程组，并通过方程组求解下一步的值。 这种需要求解方程得到下一步值的方法称为隐式方法，而 FSTC 这类可以直接计算的 格式则称为显式方法。不难想到，隐式方法的计算开销会远远高于显式方法，但可以保证更 高的精度。 §4.3 稳定性分析 在运用迭代格式进行求解之前，一般需要先进行稳定性的分析来确保迭代的有效。我们 采用常用的 von Neumman 分析方法进行考察，以此确定 ht 与 h 的基本取值。 4.3.1 von Neumman 方法 一般来说，当其他都已经固定时，任何有效的方法只要 ht 充分小都能做到稳定，但若 ht 取得过大，哪怕对于很简单的方程，也会产生无法控制的误差。例如，考虑方程 ∂C ∂t = ∂ 2C ∂x2 − ∂C ∂x (4.4) 对初值 C(0, x) = sin(x)，取 h = π 100 , ht = π 200 进行 FTCS 的前几次迭代效果如图 1 。 8

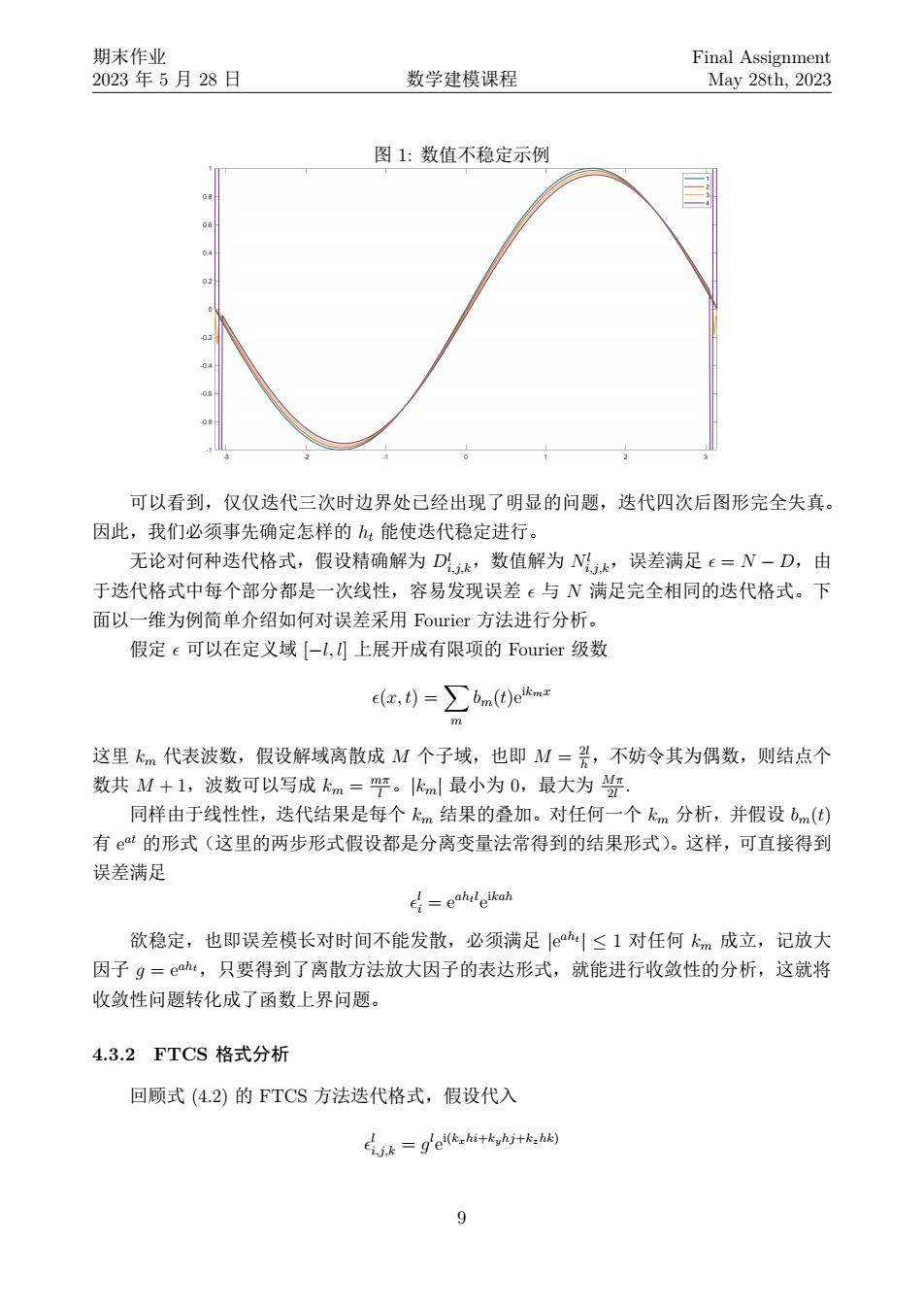
期末作业 Final Assignment 2023年5月28日 数学建模课程 May 28th,2023 图1：数值不稳定示例 可以看到，仅仅迭代三次时边界处己经出现了明显的问题，迭代四次后图形完全失真。 因此，我们必须事先确定怎样的：能使迭代稳定进行。 无论对何种迭代格式，假设精确解为D,数值解为Nk,误差满足€=N-D,由 于迭代格式中每个部分都是一次线性，容易发现误差（与N满足完全相同的迭代格式。下 面以一维为例简单介绍如何对误差采用Fourier方法进行分析。 假定e可以在定义域【-l,)上展开成有限项的Fourier级数 ctc,)=∑bn)er 这里km代表波数，假设解域离散成M个子域，也即M=兰，不妨令其为偶数，则结点个 数共M+1,波被数可以写成km=平。km最小为0，最大为竖. 同样由于线性性，迭代结果是每个km结果的叠加。对任何一个飞m分析，并假设b() 有®“的形式（这里的两步形式假设都是分离变量法常得到的结果形式）。这样，可直接得到 误差满足 c=cahlikah 欲稳定，也即误差模长对时间不能发散，必须满足le|≤1对任何km成立，记放大 因子g=eh:,只要得到了离散方法放大因子的表达形式，就能进行收敛性的分析，这就将 收敛性问题转化成了函数上界问题。 4.3.2FTCS格式分析 回顾式(4.2)的TCS方法迭代格式，假设代入 ∠k=geh+kwhi+k:h) 9

期末作业 2023 年 5 月 28 日 数学建模课程 Final Assignment May 28th, 2023 图 1: 数值不稳定示例 可以看到，仅仅迭代三次时边界处已经出现了明显的问题，迭代四次后图形完全失真。 因此，我们必须事先确定怎样的 ht 能使迭代稳定进行。 无论对何种迭代格式，假设精确解为 Dl i,j,k，数值解为 Nl i,j,k，误差满足 ϵ = N − D，由 于迭代格式中每个部分都是一次线性，容易发现误差 ϵ 与 N 满足完全相同的迭代格式。下 面以一维为例简单介绍如何对误差采用 Fourier 方法进行分析。 假定 ϵ 可以在定义域 [−l, l] 上展开成有限项的 Fourier 级数 ϵ(x, t) = ∑ m bm(t)e ikmx 这里 km 代表波数，假设解域离散成 M 个子域，也即 M = 2l h ，不妨令其为偶数，则结点个 数共 M + 1，波数可以写成 km = mπ l 。|km| 最小为 0，最大为 Mπ 2l . 同样由于线性性，迭代结果是每个 km 结果的叠加。对任何一个 km 分析，并假设 bm(t) 有 e at 的形式（这里的两步形式假设都是分离变量法常得到的结果形式）。这样，可直接得到 误差满足 ϵ l i = e ahtl e ikah 欲稳定，也即误差模长对时间不能发散，必须满足 |e aht | ≤ 1 对任何 km 成立，记放大 因子 g = e aht，只要得到了离散方法放大因子的表达形式，就能进行收敛性的分析，这就将 收敛性问题转化成了函数上界问题。 4.3.2 FTCS 格式分析 回顾式 (4.2) 的 FTCS 方法迭代格式，假设代入 ϵ l i,j,k = g l e i(kxhi+kyhj+kzhk) 9

期末作业 Final Assignment 2023年5月28日 数学建模课程 May 28th,2023 两边同时除以k可以得到 g=1+0(e-e+(e-e +e+6+46++- (4.5) 进一步化简可得 g=1+(快n动+警+2(omk小+m,刻+amk-习到 由于我们只需要确定大致量级，不妨假设（为恒定值。记A:=k/2,则收敛须 f-(停如说+兽血)(2警(om说+w说+w说-到+） (4.6) -(快m%.+血a）°+(-(r+ra+mra)°s1 、2 想要范围内此式取极大，sin6,必然为0或1，这时展开消去可得 Me血os+us电am小P-ra,+a白-P(er+a）s0 Aesa,s6,+um8os,P-Dera+sra+么-42(srg+sr2g+）s0 或写成 2h2D(sin20.+sin20.) hincosc(n+s)D2 (4.7) 2h2D(sin29.+sin29:+1) h(sin0 cosico(snsin1)D (4.8) 由h相对D,,w为小量，式(4.8)分母第一项可以别去，直接化为 么≤+a+Ds (4.9) 对式(4.7)，只要9,0.不都趋于0，分母第一项就可以删去，变为 h2 h2 ≤26in28,+sim20,PD≤4D (4.10) 而均趋于0时，分母第二项别去，|cos.=|cos0.=士1，利用柯西不等式有 sin20+sin20: 2D h,≤2Dom9.士nm9≤V+元 (4.11) 综合式(4.9)到式(4.11)得到 ≤恤{份”} 10

期末作业 2023 年 5 月 28 日 数学建模课程 Final Assignment May 28th, 2023 两边同时除以 ϵ l i,j,k 可以得到 g =1 + vht 2h ( e ikxh − e −ikxh ) + w l kht 2h ( e ikzh − e −ikzh ) + Dht h 2 ( e ikxh + e −ikxh + e ikhy + e −ikyh + e ikzh + e −ikzh − 6 ) (4.5) 进一步化简可得 g = 1 + i ( vht h sin(kxh) + w l kht h sin(kzh) ) + 2Dht h 2 ( cos(kxh) + cos(kyh) + cos(kzh) − 3 ) 由于我们只需要确定大致量级，不妨假设 w l k 为恒定值 w。记 θx,y,z = kx,y,zh/2，则收敛须 |g| 2 = ( vht h sin 2θx + wht h sin 2θz )2 + ( 2Dht h 2 ( cos 2θx + cos 2θy + cos 2θz − 3 ) + 1)2 = ( vht h sin 2θx + wht h sin 2θz )2 + ( 1 − 4Dht h 2 ( sin2 θx + sin2 θy + sin2 θz ) )2 ≤ 1 (4.6) 想要范围内此式取极大，sin2 θy 必然为 0 或 1，这时展开消去可得 ht(v sin θx cos θx + w sin θz cos θz) 2 − D(sin2 θx + sin2 θz) ( 2 − 4Dht h 2 ( sin2 θx + sin2 θz ) ) ≤ 0 ht(v sin θx cos θx+w sin θz cos θz) 2−D(sin2 θx+sin2 θz+1)( 2− 4Dht h 2 ( sin2 θx+sin2 θz+1) ) ≤ 0 或写成 ht ≤ 2h 2D(sin2 θx + sin2 θz) h 2 (v sin θx cos θx + w sin θz cos θz) 2 + 4(sin2 θx + sin2 θz) 2D2 (4.7) ht ≤ 2h 2D(sin2 θx + sin2 θz + 1) h 2 (v sin θx cos θx + w sin θz cos θz) 2 + 4(sin2 θx + sin2 θz + 1)2D2 (4.8) 由 h 相对 D, v, w 为小量，式 (4.8) 分母第一项可以删去，直接化为 ht ≤ h 2 2(sin2 θx + sin2 θz + 1)2D ≤ h 2 6D (4.9) 对式 (4.7)，只要 θx, θz 不都趋于 0，分母第一项就可以删去，变为 ht ≤ h 2 2(sin2 θx + sin2 θz) 2D ≤ h 2 4D (4.10) 而均趋于 0 时，分母第二项删去，| cos θx| = | cos θz| = ±1，利用柯西不等式有 ht ≤ 2D sin2 θx + sin2 θz (v sin θx ± w sin θz) 2 ≤ 2D √ v 2 + w2 (4.11) 综合式 (4.9) 到式 (4.11) 得到 ht ≤ min { h 2 6D , 2D √ v 2 + w2 } 10

期末作业 Final Assignment 2023年5月28日 数学建模课程 May 28th,2023 考虑到：为小量，一般只需要满足第一个限制即可，由于上方忽略了部分小量的影响， 实际分母系数应比6稍大。类似地，对一维有风情况可以推出：≤min{品，}，二维且 有某方向风时结果是h,≤min{元，P}。一般结果为n维时： (4.12) 4.3.3C-N格式分析 与FTCS相比，CN格式的稳定性反而较为简单。记 A=(ak+)+2(ok+s+mk- 则代入C-N格式后有 g=1+4+9g= 因此直接设A=a+i计算可得 lg≤1÷ReA≤0 而这也就意味着 2(ak小+)+em化小-9≤0 (4.13) 由于式(4.13)恒成立，CN格式是恒稳定的。这也揭示了它在误差阶小之外的优势。因 此，在利用CN格式进行迭代时，可以将时间步长提升，仍能达到较好的效果。 五、求解方案选择 在上一节，我们确定了不同有限差分法的稳定条件，于是可以构造差分求解。但是，在 求解过程中，仍然有很多细节问题需要处理，本节主要介绍模拟边界而非真实边界的“伪边 界”处理与C-N格式的实际实现。 S5.1伪边界处理 5.1.1一维问题 考虑一维的对流扩散方程： ac (5.1) 进行预处理 U=U ht h/2; D=D*ht/h2； 11

期末作业 2023 年 5 月 28 日 数学建模课程 Final Assignment May 28th, 2023 考虑到 ht 为小量，一般只需要满足第一个限制即可，由于上方忽略了部分小量的影响， 实际分母系数应比 6 稍大。类似地，对一维有风情况可以推出 ht ≤ min { h 2 2D , 2D v } ，二维且 有某方向风时结果是 ht ≤ min { h 2 4D , 2D v } 。一般结果为 n 维时： ht ≤ min { h 2 2nD , 2D ∥u∥ } (4.12) 4.3.3 C-N 格式分析 与 FTCS 相比，C-N 格式的稳定性反而较为简单。记 A = i ( vht h sin(kxh) + w l kht h sin(kzh) ) + 2Dht h 2 ( cos(kxh) + cos(kyh) + cos(kzh) − 3 ) 则代入 C-N 格式后有 g = 1 + 1 2 (A + gA) ⇔ g = 1 + A/2 1 − A/2 因此直接设 A = a + bi 计算可得 |g| ≤ 1 ⇔ ReA ≤ 0 而这也就意味着 2Dht h 2 ( cos(kxh) + cos(kyh) + cos(kzh) − 3 ) ≤ 0 (4.13) 由于式 (4.13) 恒成立，C-N 格式是恒稳定的。这也揭示了它在误差阶小之外的优势。因 此，在利用 C-N 格式进行迭代时，可以将时间步长提升，仍能达到较好的效果。 五、 求解方案选择 在上一节，我们确定了不同有限差分法的稳定条件，于是可以构造差分求解。但是，在 求解过程中，仍然有很多细节问题需要处理，本节主要介绍模拟边界而非真实边界的“伪边 界”处理与 C-N 格式的实际实现。 §5.1 伪边界处理 5.1.1 一维问题 考虑一维的对流扩散方程： ∂C ∂t = D ∂ 2C ∂x2 − U ∂C ∂x (5.1) 进行预处理 U = U * ht / h / 2; D = D * ht / h ^ 2; 11