
附件24.2 Chapter2 Fundamental Hydraulic Fluid Mechanics 2.The definition of pressure (1)Absolute pressure (2)Relative gauge pressure:The pressures measured by a pressure gauge are all relative pressure (3)Vacuum (negative pressure) The units of pressure and relations between different pressures 1Pa=1N/m2:1bar=1X103Pa=1X109N/m2; 1at=1kgf/cm2=9.8×104N/m2:1mH,0-9.8×103N/m2 1mmHg=1.33X103N/m2 The relationship of three pressures is shown in Fig.2-5 Hrorog List Uperdks Dornveards Peciam Edit Chapter2 Fundamental Hydranlic Fluid Mechanies -p>Pa Gauge pressure (表压力) p<pe A时空 Fig.2-5 absolute,relative and vacuum pressure
附件 24.2 14

附件242 Chapter2 Fundamental Hydranlic Flnid Mechanies Example 2-1:The oil is full in a coutainer.For a given condition:the density of oil o=900(kg/ur),the action force on this pistou surface F=10000N). the area of piston A=).if the mass of piston is neglected,try to calculate the static pressure p at h=0.5m,as shown in Fig.2-6. 工 Fig.2-6 Calculation of fluid static pressure 2.2.3 The principle of Pascal application The principle of Pascal mndiminished in all directions and acts with equal force on all equal areas Its application is shown in Fig.2-7. Fig.2-7 The examnple of Pascal principle applicat
附件 24.2 15

附件24.2 Chapter2 Fundamental Hydranlie Fluid Mechanics 女。 2.2.4 Effect of fluid pressure on curved surfaces (1)When the wall is plane F=P.A (2)When wall is a curved surface: Example 2-2.Fig.2-8 shows a cylindrical member of inside radii r of length/. Calculation:the effect force F on the right segment of the cylinder at x direction Fig.2-8 Effect force on the inuer surface of the cylinder Homework:pp.349 Chapter 2,2-1,2-2,2-3,2-4. 2.3 Hydrodynamies(液体动力学) Chapter2 Fundamental Hydraulic Fluid Mechanics The equations of continuity,Bernoulli and momentum are basic motion equations that describe the dynamics laws in flowing fluid 2.3.1 The equation of continuity-conservation of mass according to the conservation of mass. A4=P2A2214) incompressible flow.P=P2.(2-15) VA=VA Fig.2-9 sketch of conservation Or q==v242 =v.4=constant (2-16) Formula(2-16)is the equation of flow coutinuity
附件 24.2 Homework: pp.349 Chapter 2, 2-1, 2-2, 2-3, 2-4. 2.3 Hydrodynamics (液体动力学) 16
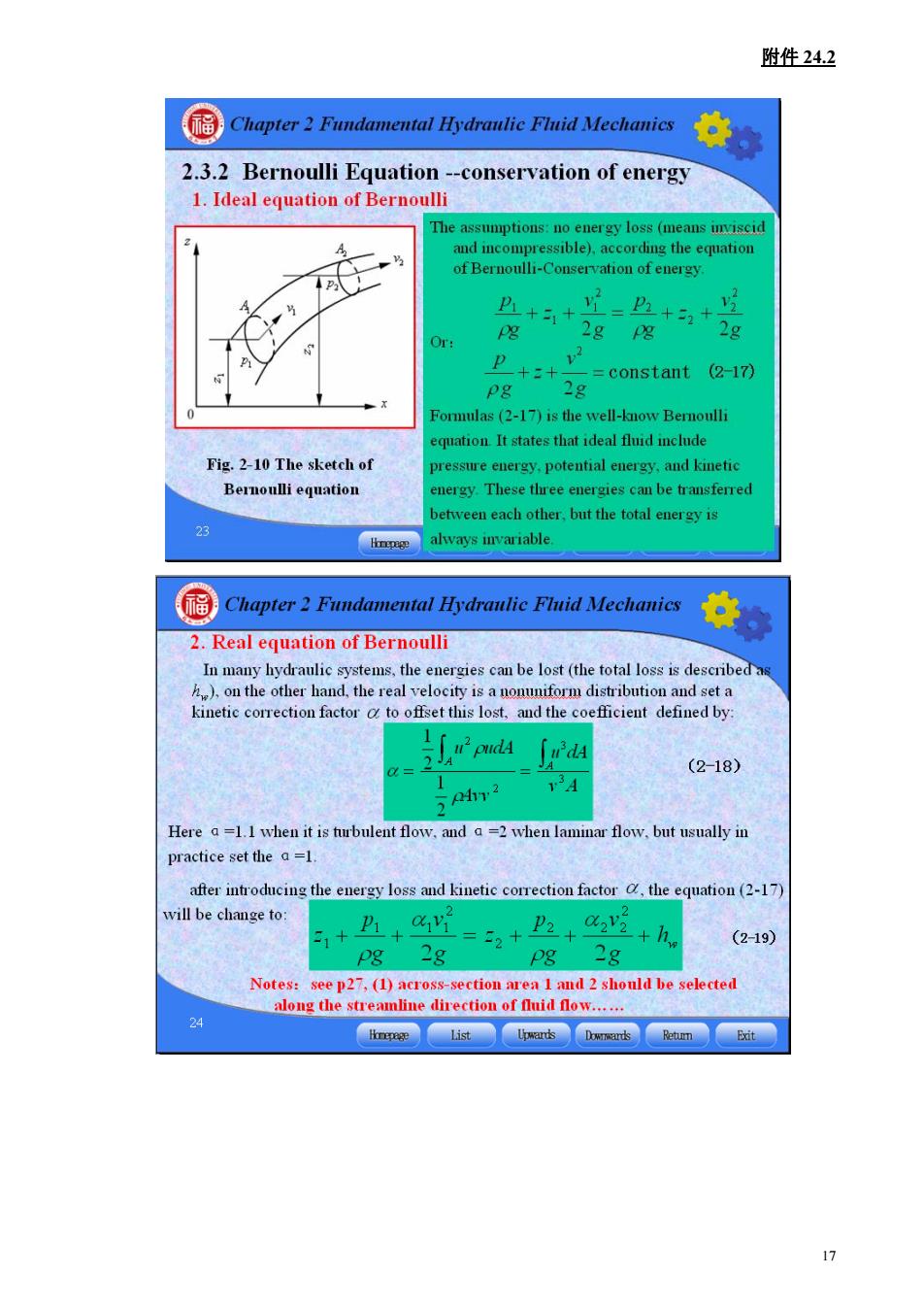
附件242 Chapter2 Fundamental Hydraulie Flnid Mechanies 2.3.2 Bernoulli Equation -conservation of energy 1.Ideal equation of Bernoulli of bernoulli-Conservation of enerey 、 +a+2g +*2g% +2g-constant omulas (2-17)is the well-know Bernoulli states that ideal fluid includ Fig.2-10 The sketch of oressure energy.potential energy.and kinetic Bernoulli equation energy These three energies can be transferred etween the total energy 2.Real equation of Bernoulli In mauy hydraulic systems the energies can be lost (the total loss is described )on the other hand.the real velocity is a nonuniform distribution and set a kinetic correction factor to offset this lost and the coefcient defied by (2-18) 13A Here a=1.1 when it is tubulent flow,and a=2 when laminar flow,but usually in practice set the a=1. after introducing the energy loss and kinetic correction factor the equation(2-17) vill be change to: =+++h (2-19) pg 2g pg 28 Notes:see p27,(1)across-section ar aI and 2 should be selected along the streamline direction of fluid flow
附件 24.2 17

附件24.2 3.Application example of the equation of Bernouthi 2-3Te Fig.2-11 Venture meter Chapter 2 Fundamental Hydraulic Fluid Mechanies Example 2-4.Try to analyse the condition of a pump drawing mnte oil from a reservoir by the equation of Bernoulli (Fig.2-12).Set the pressure at 2-2 across-section is p the pressure at 1-1 across-section ispr and PP and the distance from pump orifice to hydraulic oil surface is Fig.2-12 Setup of hydraulic pump
附件 24.2 18