
FEM-Chapter 8 Practical modeling Issues
FEM - Chapter 8 Practical modeling Issues

Nature of Finite Element Solutions FE Model-A mathematical model of the real structure,based on many approximations. Real Structures-Infinite number of nodes(physical points),thus infinite number of DOFs. FE Model-finite number of nodes,thus finite number DOFs. Displacement field is controlled by the shape functions and the values at a limited number of nodes. Stiffening Effect: FE model is stiffer than the real structure. In general,displacement results are smaller in magnitudes than the exact values
Nature of Finite Element Solutions • FE Model – A mathematical model of the real structure, based on many approximations. • Real Structures – Infinite number of nodes (physical points), thus infinite number of DOFs. • FE Model – finite number of nodes, thus finite number DOFs. • Displacement field is controlled by the shape functions and the values at a limited number of nodes. Stiffening Effect: • FE model is stiffer than the real structure. • In general, displacement results are smaller in magnitudes than the exact values

Common Sources of Error in FEA Controllable factors Domain approximation Element interpolation/Approximation Uncontrollable factors Numerical integration errors(Both spatial and time integration) Computer errors(Round-ff,etc.) Cause for incorrect results: ·Mistakes ·errors
Common Sources of Error in FEA - Controllable factors • Domain approximation • Element interpolation/Approximation - Uncontrollable factors • Numerical integration errors (Both spatial and time integration) • Computer errors(Round-ff, etc.) - Cause for incorrect results: • Mistakes • errors

Common Mistakes Mistakes that will cause a singular K matrix: -v=0.5 in a plain strain,axisymmetric or 3D solid element -E=0 in an element -Unconnected nodes -No supports,or insufficient supports -Part of the model is a mechanism -Large stiffness differences
Common Mistakes Mistakes that will cause a singular K matrix: – ν = 0.5 in a plain strain, axisymmetric or 3D solid element – E = 0 in an element – Unconnected nodes – No supports, or insufficient supports – Part of the model is a mechanism – Large stiffness differences
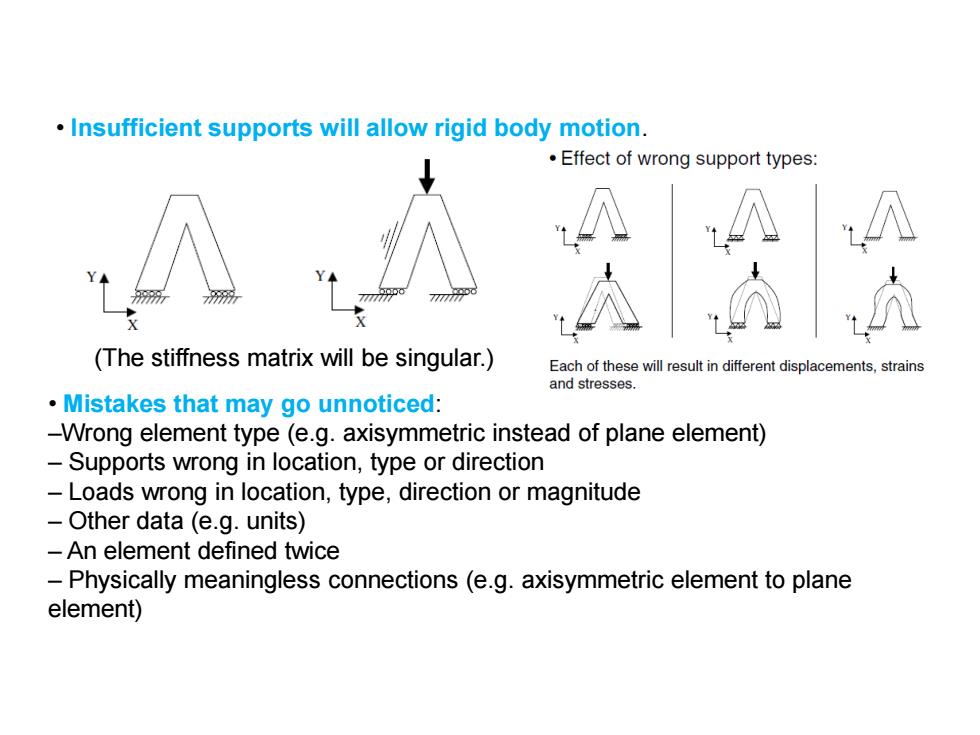
Insufficient supports will allow rigid body motion. Effect of wrong support types: (The stiffness matrix will be singular.) Each of these will result in different displacements,strains and stresses. Mistakes that may go unnoticed: -Wrong element type(e.g.axisymmetric instead of plane element) Supports wrong in location,type or direction Loads wrong in location,type,direction or magnitude Other data (e.g.units) -An element defined twice -Physically meaningless connections(e.g.axisymmetric element to plane element)
• Insufficient supports will allow rigid body motion. (The stiffness matrix will be singular.) • Mistakes that may go unnoticed: –Wrong element type (e.g. axisymmetric instead of plane element) – Supports wrong in location, type or direction – Loads wrong in location, type, direction or magnitude – Other data (e.g. units) – An element defined twice – Physically meaningless connections (e.g. axisymmetric element to plane element)