宣城市工业学校：《电子线路》课程教学资源（试题习题）组合逻辑电路（含解答）

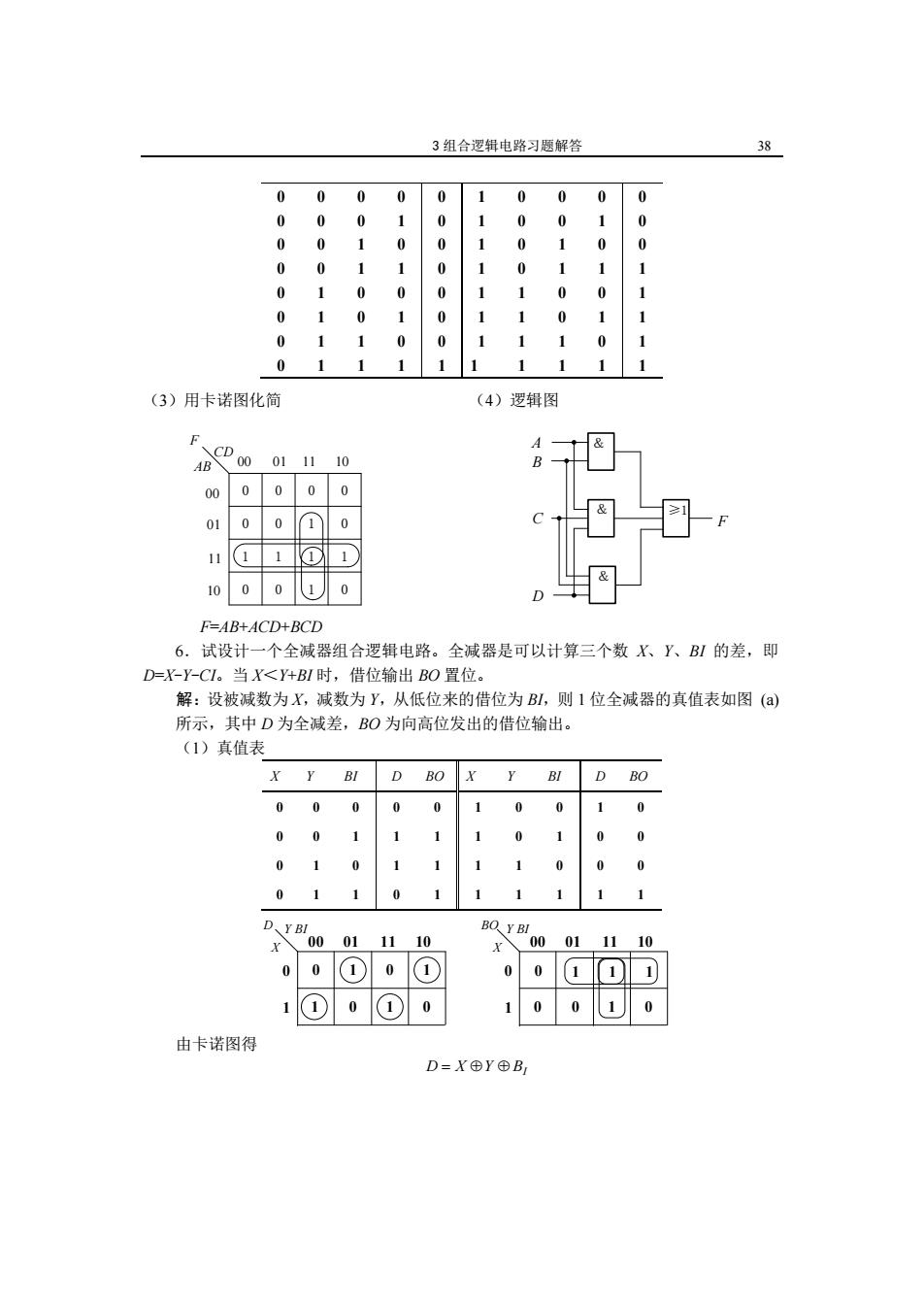
3组合逻辑电路习题解答 38 0 00 S 1 0 0 0 0 000 1 0 001 0 0 1 0 1 0 0 001 1 1 S 1 1 01 0 0 0 1 1 0 0 1 0 10 1 S 0 1 0 11 0 0 1 1 1 0 1 0 1 1 1 (3)用卡诺图化简 (4)逻辑图 F CD AB 00 01 1110 00 0 0 0 01 0 0 0 11 1 10 0 0 0 F=AB+ACD+BCD 6.试设计一个全减器组合逻辑电路。全减器是可以计算三个数X、Y、B1的差，即 D=X-Y-CI。当X<Y+BI时，借位输出BO置位。 解：设被减数为X,减数为Y,从低位来的借位为BL,则1位全减器的真值表如图() 所示，其中D为全减差，BO为向高位发出的借位输出。 (1)真值表 X Y BI D BO BI D BO 00 0 0 1 00 1 1 1 1 1 0 0 0 1 0 1 1 1 0 0 0 1 1 0 1 1 D、YBI BO Y BI 、00 0111 10 X 00 011110 0 (1) (1 0 0 1 ①0 0 1 00 10 由卡诺图得 D=X⊕Y⊕B

3 组合逻辑电路习题解答 38 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 0 0 0 1 1 1 1 1 （3）用卡诺图化简 （4）逻辑图 AB00CD 011110 00 01 11 10 F 0 0 0 0 0 0 1 0 1 1 1 1 0 0 1 0 BC A ＆ ＆ ≥1 F D ＆ BC A ＆ ＆ ≥1 F D ＆ F=AB+ACD+BCD 6．试设计一个全减器组合逻辑电路。全减器是可以计算三个数 X、Y、BI 的差，即 D=X-Y-CI。当 X＜Y+BI 时，借位输出 BO 置位。 解：设被减数为 X，减数为 Y，从低位来的借位为 BI，则 1 位全减器的真值表如图 (a) 所示，其中 D 为全减差，BO 为向高位发出的借位输出。 （1）真值表 X Y BI D BO X Y BI D BO 0 0 0 0 0 1 0 0 1 0 0 0 1 1 1 1 0 1 0 0 0 1 0 1 1 1 1 0 0 0 0 1 1 0 1 1 1 1 1 1 0 1 0 1 1 0 1 0 0 1 00 01 11 10 X D Y BI 0 1 1 1 0 0 1 0 0 1 00 01 11 10 X Y BI BO 由卡诺图得 D  X Y  BI

3组合逻辑电路习题解答 39 Bo =YB +XB+XY 电路图 7.设计组合逻辑电路，将4位无符号二进制数转换成格雷码。 解：(1)列出4位二进制码→4位格雷码的转换真值表，如表所示。 家 入 委 西 频 入 香 出 B3 B2 B1 Bo G3 G2 G1 Go B3 B2 B1 Bo G3 G2G1 Go 0 0 0 0 0 0 0 0 0 0 1 1 0 00 0 1 0 0 0 1 1 0 0 1 1 1 0 1 0 0 1 0 0 0 1 0 1 0 1 1 1 1 00 1 1 0 0 1 0 1 0 1 1 11 1 0 010 0 0 1 1 0 1 1 0 0 1 01 0 010 1 1 1 0 01 0110 0 1 0 1 1 1 0 100 1 01 0 0 0 0 0 (2)根据真值表分别画出输出变量G3,G2,G,G的卡诺图，如图4.1.2-12所示。化 简后，得 G3=B3,G2=B3⊕B2,G1=B2⊕B1,G0=B1⊕B0 G2、B1B0 G1、B1B0 Go、B1Bo B:B2 00011110 B:B2 、00011110 00 011110 B:B2 00 0 0 00 0 0 1 00 0 01 (11 01 0 10 111 0 10 (3)由逻辑表达式得电路实现，如图所示

3 组合逻辑电路习题解答 39 BO  YBI  X BI  XY 电路图 & =1 Y X D BO =1 BI & & ≥1 1 7．设计组合逻辑电路，将 4 位无符号二进制数转换成格雷码。 解：（1）列出 4 位二进制码→4 位格雷码的转换真值表，如表所示。 输 入 输 出 输 入 输 出 B3 B2 B1 B0 G3 G2 G1 G0 B3 B2 B1 B0 G3 G2 G1 G0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0 0 0 0 0 1 0 0 0 1 1 0 0 1 1 1 0 1 0 0 1 0 0 0 1 1 1 0 1 0 1 1 1 1 0 0 1 1 0 0 1 0 1 0 1 1 1 1 1 0 0 1 0 0 0 1 1 0 1 1 0 0 1 0 1 0 0 1 0 1 0 1 1 1 1 1 0 1 1 0 1 1 0 1 1 0 0 1 0 1 1 1 1 0 1 0 0 1 0 1 1 1 0 1 0 0 1 1 1 1 1 0 0 0 （2）根据真值表分别画出输出变量 G3，G2，G1，G0的卡诺图，如图 4.1.2-12 所示。化 简后，得 G3  B3 ，G2  B3  B2，G1  B2  B1，G0  B1  B0 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 00 01 10 11 00 01 11 10 B3B2 G2 B1B0 0 0 1 1 1 1 0 0 1 1 0 0 0 0 1 1 00 01 10 11 00 01 11 10 B3B2 G1 B1B0 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 00 01 10 11 00 01 11 10 B3B2 G0 B1B0 （3）由逻辑表达式得电路实现，如图所示

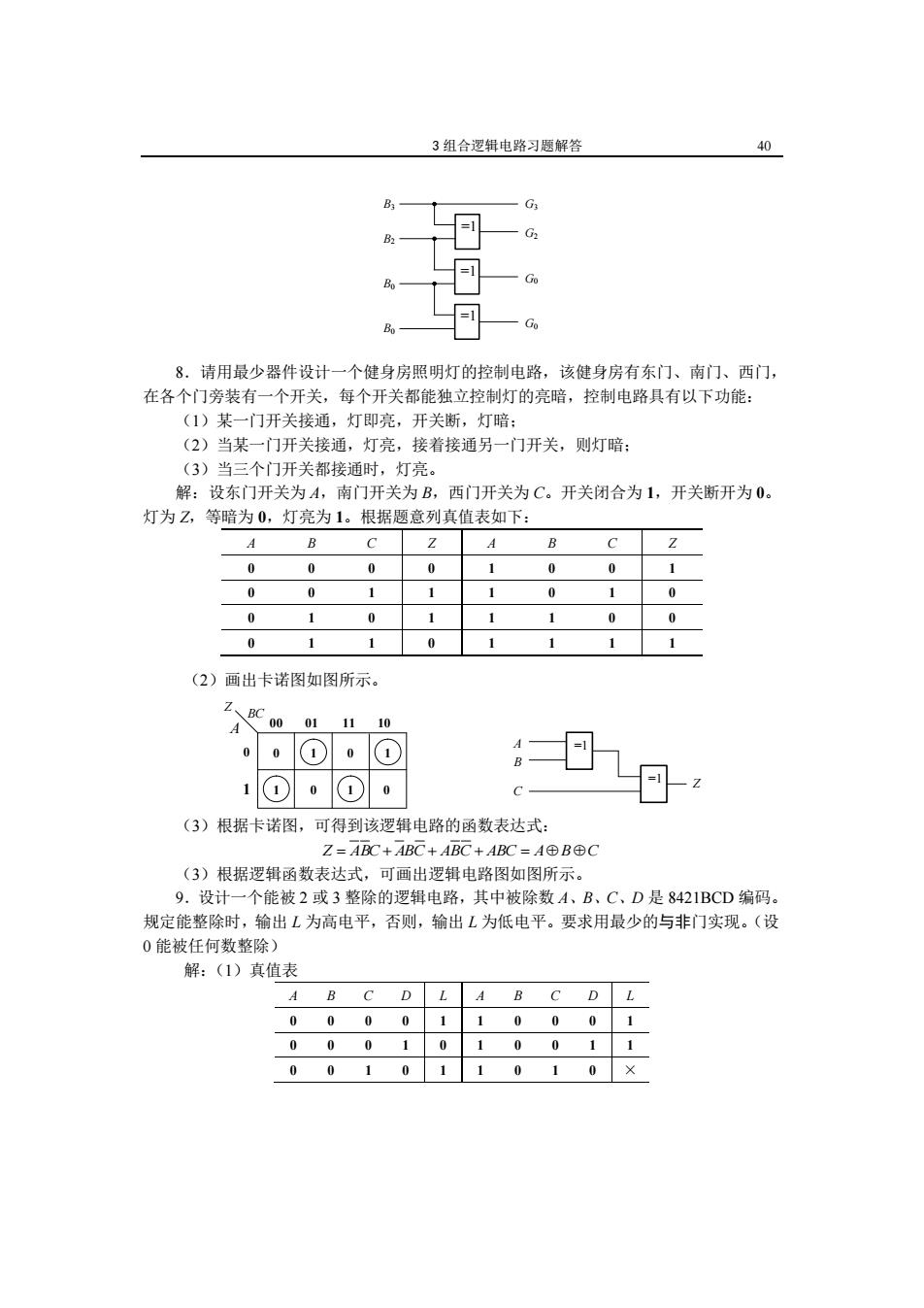
3组合逻辑电路习题解答 40 B G 8.请用最少器件设计一个健身房照明灯的控制电路，该健身房有东门、南门、西门， 在各个门旁装有一个开关，每个开关都能独立控制灯的亮暗，控制电路具有以下功能： (1)某一门开关接通，灯即亮，开关断，灯暗： (2)当某一门开关接通，灯亮，接着接通另一门开关，则灯暗： (3)当三个门开关都接通时，灯亮。 解：设东门开关为A,南门开关为B,西门开关为C。开关闭合为1，开关断开为0。 灯为Z,等暗为0，灯亮为1。根据题意列真值表如下： A B C Z A B C Z 0 0 1 0 0 0 0 1 1 1 0 1 0 1 0 1 1 0 0 0 (2)画出卡诺图如图所示。 Z、BC 0001 11 (3)根据卡诺图，可得到该逻辑电路的函数表达式： Z=ABC+ABC+ABC+ABC=A⊕B⊕C (3)根据逻辑函数表达式，可画出逻辑电路图如图所示。 9.设计一个能被2或3整除的逻辑电路，其中被除数A、B、C、D是8421BCD编码。 规定能整除时，输出L为高电平，否则，输出L为低电平。要求用最少的与非门实现。（设 0能被任何数整除) 解：(1)真值表 AB C D L L 0000 1 0.00 000 1 0 1 001 0 010 1 1 0 10

3 组合逻辑电路习题解答 40 =1 =1 =1 B3 B2 B0 B0 G3 G2 G0 G0 8．请用最少器件设计一个健身房照明灯的控制电路，该健身房有东门、南门、西门， 在各个门旁装有一个开关，每个开关都能独立控制灯的亮暗，控制电路具有以下功能： （1）某一门开关接通，灯即亮，开关断，灯暗； （2）当某一门开关接通，灯亮，接着接通另一门开关，则灯暗； （3）当三个门开关都接通时，灯亮。 解：设东门开关为 A，南门开关为 B，西门开关为 C。开关闭合为 1，开关断开为 0。 灯为 Z，等暗为 0，灯亮为 1。根据题意列真值表如下： A B C Z A B C Z 0 0 0 0 1 0 0 1 0 0 1 1 1 0 1 0 0 1 0 1 1 1 0 0 0 1 1 0 1 1 1 1 （2）画出卡诺图如图所示。 0 1 0 1 1 0 1 0 0 1 00 01 11 10 A BC Z =1 =1 A Z B C （3）根据卡诺图，可得到该逻辑电路的函数表达式： Z  ABC  ABC  ABC  ABC  ABC （3）根据逻辑函数表达式，可画出逻辑电路图如图所示。 9．设计一个能被 2 或 3 整除的逻辑电路，其中被除数 A、B、C、D 是 8421BCD 编码。 规定能整除时，输出 L 为高电平，否则，输出 L 为低电平。要求用最少的与非门实现。（设 0 能被任何数整除） 解：（1）真值表 A B C D L A B C D L 0 0 0 0 1 1 0 0 0 1 0 0 0 1 0 1 0 0 1 1 0 0 1 0 1 1 0 1 0 ×

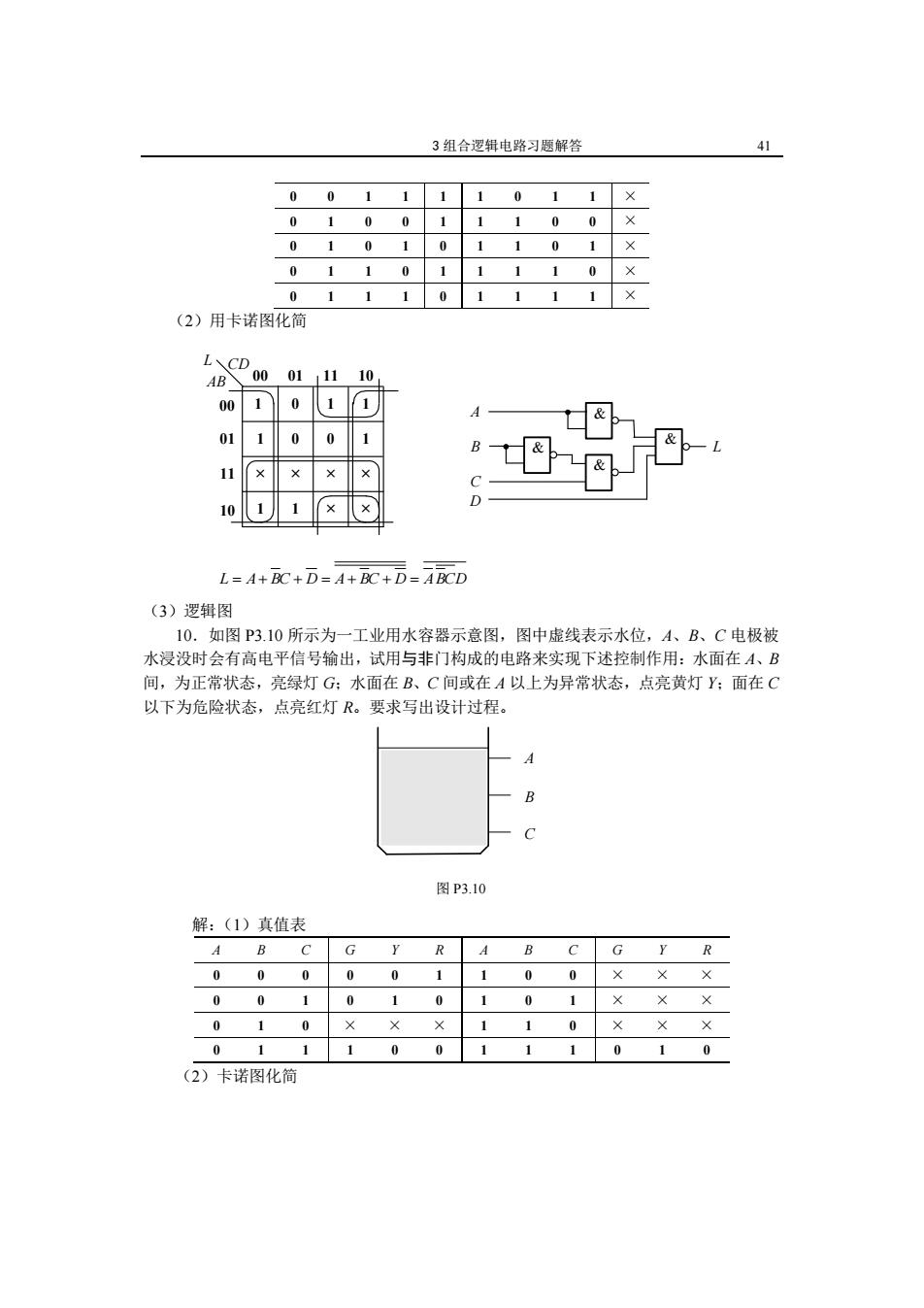
3组合逻辑电路习题解答 41 0 01 1 1 01 00 1 1 1 0 0× 0101 0 1 1 0 1 0110 1 1 1 1 0 0111 0 1 1 (2)用卡诺图化简 LCD AB 0001,11 10 00 1 01 1 0 11 D 10 L=A+BC+D=A+BC+D=ABCD (3)逻辑图 10.如图P3.10所示为一工业用水容器示意图，图中虚线表示水位，A、B、C电极被 水浸没时会有高电平信号输出，试用与非门构成的电路来实现下述控制作用：水面在A、B 间，为正常状态，亮绿灯G:水面在B、C间或在A以上为异常状态，点亮黄灯Y:面在C 以下为危险状态，点亮红灯R。要求写出设计过程。 图P3.10 解：(1)真值表 G B C G y 00 0 0 01 00 00 1 0 1 0 1 0 1 010 1 0 01 11 0 0 1 1 1 0 1 0 (2)卡诺图化简

3 组合逻辑电路习题解答 41 0 0 1 1 1 1 0 1 1 × 0 1 0 0 1 1 1 0 0 × 0 1 0 1 0 1 1 0 1 × 0 1 1 0 1 1 1 1 0 × 0 1 1 1 0 1 1 1 1 × （2）用卡诺图化简 1 0 1 1 1 0 0 1 × × × × 1 1 × × 00 01 11 10 00 01 11 10 AB L CD & & B & D & C A L L  A BC  D  A BC  D  ABCD （3）逻辑图 10．如图 P3.10 所示为一工业用水容器示意图，图中虚线表示水位，A、B、C 电极被 水浸没时会有高电平信号输出，试用与非门构成的电路来实现下述控制作用：水面在 A、B 间，为正常状态，亮绿灯 G；水面在 B、C 间或在 A 以上为异常状态，点亮黄灯 Y；面在 C 以下为危险状态，点亮红灯 R。要求写出设计过程。 A B C 图 P3.10 解：（1）真值表 A B C G Y R A B C G Y R 0 0 0 0 0 1 1 0 0 × × × 0 0 1 0 1 0 1 0 1 × × × 0 1 0 × × × 1 1 0 × × × 0 1 1 1 0 0 1 1 1 0 1 0 （2）卡诺图化简

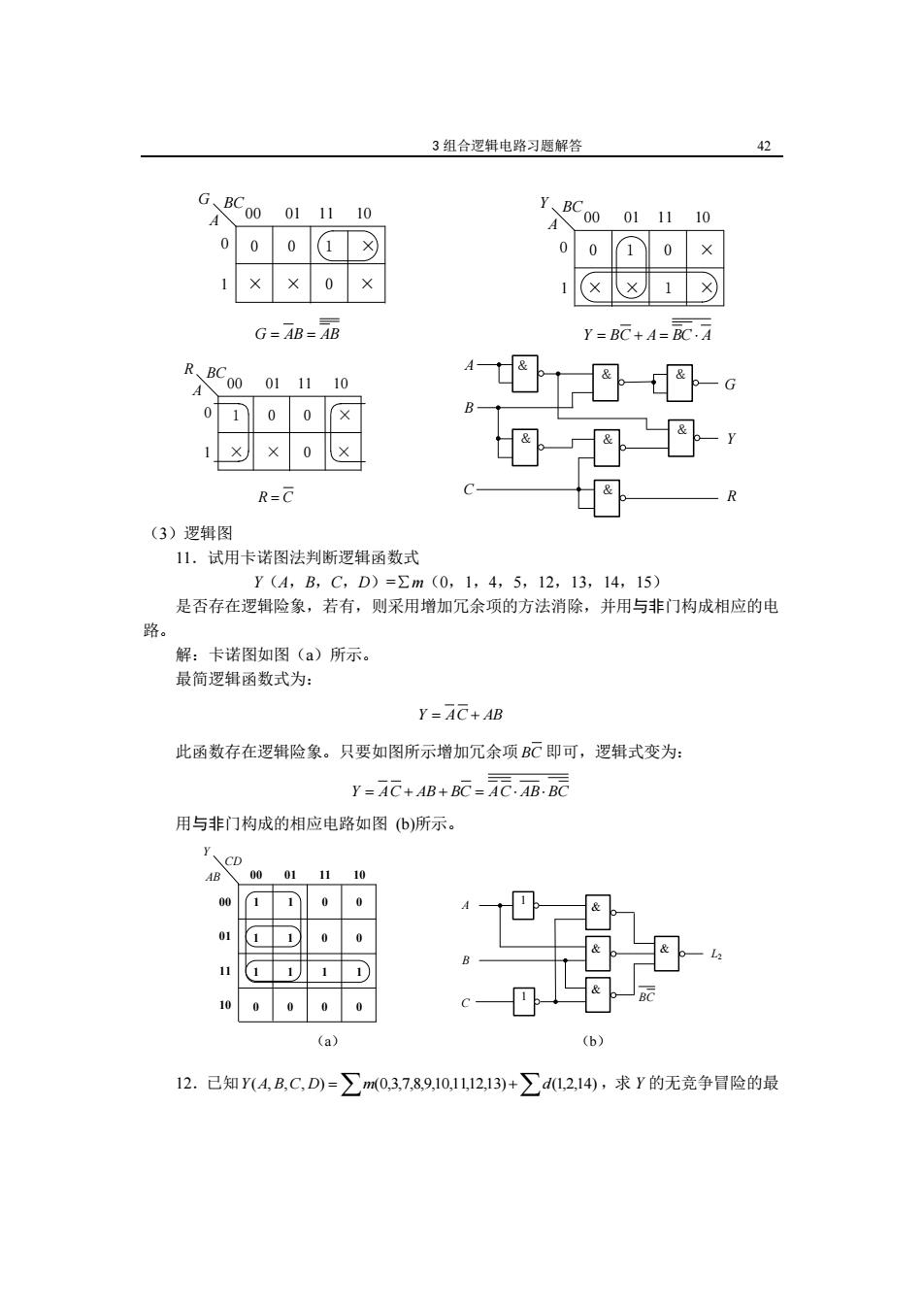
3组合逻辑电路习题解答 42 G、BC A八 00 0111 10 Y、BC A 00 01 11 10 0 0 0 1 0 0 1 0 × 1 0 (×1 G=AB=AB Y=BC+A=BC.A R、BC 00 0111 A 10 0 十 0 R-C (3)逻辑图 11.试用卡诺图法判断逻辑函数式 Y(A,B,C,D)=∑m(0,1,4,5,12,13,14,15) 是否存在逻辑险象，若有，则采用增加冗余项的方法消除，并用与非门构成相应的电 路。 解：卡诺图如图(a)所示。 最简逻辑函数式为： Y=AC+AB 此函数存在逻辑险象。只要如图所示增加冗余项BC即可，逻辑式变为： Y=AC+AB+BC=AC.AB.BC 用与非门构成的相应电路如图(b)所示。 Y CD AB 00 01 11 10 00 01 0 0 0 (a) (b) 12.己知Y(4,B,C,D)-∑m03,7,89,10,1112,13)+∑d12,14),求Y的无竞争冒险的最

3 组合逻辑电路习题解答 42 A 0 BC1 00 01 11 10 Y 0 1 0 × × × × A 0 BC1 00 01 11 10 G 0 0 1 × × × 0 × G  AB  AB 1 Y  BC  A  BC  A A 0 BC1 00 01 11 10 R 1 0 0 × × × 0 × BC A ＆ ＆ G ＆ R  C Y ＆ R ＆ ＆ ＆ （3）逻辑图 11．试用卡诺图法判断逻辑函数式 Y（A，B，C，D）=∑m（0，1，4，5，12，13，14，15） 是否存在逻辑险象，若有，则采用增加冗余项的方法消除，并用与非门构成相应的电 路。 解：卡诺图如图（a）所示。 最简逻辑函数式为： Y  AC  AB 此函数存在逻辑险象。只要如图所示增加冗余项 BC 即可，逻辑式变为： Y  AC  AB  BC  AC ABBC 用与非门构成的相应电路如图 (b)所示。 & & & A L2 C 1 AB 00 01 11 10 CD 00 01 11 10 1 0 0 1 1 0 0 1 1 1 1 0 0 0 0 Y & B 1 1 BC （a） （b） 12．已知 Y(A, B,C, D) m(0,3,7,8,9,10,11,12,13) d(1,2,14) ，求 Y 的无竞争冒险的最