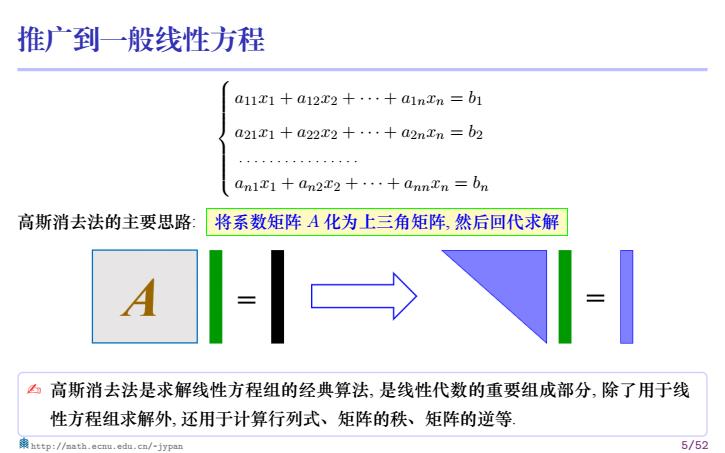
推广到一般线性方程 a1121 a12x2++ainEn 61 a211+a22x2+...+a2n.tn b2 anlc1+an2x2+··+annEn=bn 高斯消去法的主要思路: 将系数矩阵A化为上三角矩阵,然后回代求解 A 凸高斯消去法是求解线性方程组的经典算法,是线性代数的重要组成部分,除了用于线 性方程组求解外,还用于计算行列式、矩阵的秩、矩阵的逆等 http://math.ecnu.edu.cn/-jypan 5/52
推广到一般线性方程 a11x1 + a12x2 + · · · + a1nxn = b1 a21x1 + a22x2 + · · · + a2nxn = b2 . . . . . . . . . . . . . . . . an1x1 + an2x2 + · · · + annxn = bn 高斯消去法的主要思路: 将系数矩阵 A 化为上三角矩阵, 然后回代求解 ✍ 高斯消去法是求解线性方程组的经典算法, 是线性代数的重要组成部分, 除了用于线 性方程组求解外, 还用于计算行列式、矩阵的秩、矩阵的逆等. http://math.ecnu.edu.cn/~jypan 5/52

2-1-1 Gauss消去过程 多写出相应算法,并编程实现 记增广矩阵 ) (1) 1) 011 012 0 (1) 022 (1) A)= 0 州 a ) ann 其中 =0j b=b, i,j=1,2,,n http://nath.ecnu.edu.cn/-jypan 6/52
2-1-1 Gauss 消去过程 写出相应算法, 并编程实现 记增广矩阵 A (1) = a (1) 11 a (1) 12 · · · a (1) 1n b (1) 1 a (1) 21 a (1) 22 · · · a (1) 2n b (1) 2 . . . . . . . . . . . . . . . a (1) n1 a (1) n2 · · · a (1) nn b (1) n , 其中 a (1) ij = aij , b(1) i = bi , i, j = 1, 2, . . . , n. http://math.ecnu.edu.cn/~jypan 6/52

第1步:消第1列 (1) 设唱≠0,计算1=霜i=2,3n对增广矩阵A0进行n-1次初等变换,即 011 依次将A1)的第i行(i>1)减去第1行的l1倍,将新得到的矩阵记为A②),即 (1) a12 (2) (2) A② 022 02m g 品 其中 =9-l1,b2=6-ab吧,ij=2,3n 00 http://math.ecnu.edu.cn/-jypan 7/52
第 1 步: 消第 1 列. 设 a (1) 11 ̸= 0 , 计算 li1 = a (1) i1 a (1) 11 , i = 2, 3, . . . , n. 对增广矩阵 A(1) 进行 n − 1 次初等变换, 即 依次将 A(1) 的第 i 行 (i > 1) 减去第 1 行的 li1 倍, 将新得到的矩阵记为 A(2) , 即 A (2) = a (1) 11 a (1) 12 · · · a (1) 1n b (1) 1 a (2) 22 · · · a (2) 2n b (2) 2 . . . . . . . . . . . . a (2) n2 · · · a (2) nn b (2) n , 其中 a (2) ij = a (1) ij − li1a (1) 1j , b(2) i = b (1) i − li1b (1) 1 , i, j = 2, 3, . . . , n. http://math.ecnu.edu.cn/~jypan 7/52

第2步:消第2列 (2) 设a2≠0,计算l2= ,i=34…n 依次将A②的第i行(i>2)减去第2行的 02 l2倍,将新得到的矩阵记为A③),即 a .(1) (1) 012 唱 01 四 (2) (2 (2) d22 023 02 A3)= ) 033 (2) a侧 a 周 其中 g=号-l号,6=9-lab2,ij=3,4,n http://math.ecnu.edu.cn/-jypan 8/52
第 2 步: 消第 2 列. 设 a (2) 22 ̸= 0 , 计算 li2 = a (2) i2 a (2) 22 , i = 3, 4, . . . , n. 依次将 A(2) 的第 i 行 (i > 2) 减去第 2 行的 li2 倍, 将新得到的矩阵记为 A(3) , 即 A (3) = a (1) 11 a (1) 12 a (1) 13 · · · a (1) 1n b (1) 1 a (2) 22 a (2) 23 · · · a (2) 2n b (2) 2 a (2) 33 · · · a (2) 3n b (3) 3 . . . . . . . . . . . . a (3) n3 · · · a (3) nn b (3) n , 其中 a (3) ij = a (2) ij − li2a (2) 2j , b(3) i = b (2) i − li2b (2) 2 , i, j = 3, 4, . . . , n. http://math.ecnu.edu.cn/~jypan 8/52

依此类推,经过k-1步后,可得新矩阵A(): .(1) (1) 01k A(k)= () () akk akn (2.1) a限 恩 第k步:消第k列, () 设Q手0,开算:资三大+L候次将4的的第i行>)减去第至 的1:倍,将新得到的矩阵记为Ak+1),矩阵元素的更新公式为 ag+=a9-au周,6+=b-lb,i,j=k+1,k+2,n. (2.2) http://math.ecnu.edu.cn/-jypan 9/52
依此类推, 经过 k − 1 步后, 可得新矩阵 A(k) : A (k) = a (1) 11 · · · a (1) 1k · · · a (1) 1n b (1) 1 . . . . . . . . . . . . a (k) kk · · · a (k) kn b (k) k . . . . . . . . . . . . a (k) nk · · · a (k) nn b (k) n , (2.1) 第 k 步: 消第 k 列. 设 a (k) kk ̸= 0 , 计算 lik = a (k) ik a (k) kk , i = k + 1, . . . , n. 依次将 A(k) 的第 i 行 (i > k) 减去第 k 行 的 lik 倍, 将新得到的矩阵记为 A(k+1) , 矩阵元素的更新公式为 a (k+1) ij = a (k) ij − lika (k) kj , b(k+1) i = b (k) i − likb (k) k , i, j = k + 1, k + 2, . . . , n. (2.2) http://math.ecnu.edu.cn/~jypan 9/52